Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Метод прямоугольников

Метод прямоугольников – это, пожалуй, самый простой метод приближённого вычисления определённого интеграла. И парадокс состоит в том, что по этой причине (видимо) он довольно редко встречается на практике. Неудивительно, что данная статья появилась на свет через несколько лет после того, как я рассказал о более распространённых методах трапеции и Симпсона, где упомянул о прямоугольниках лишь вскользь. Однако на сегодняшний день раздел об интегралах практически завершён и поэтому настало время закрыть этот маленький пробел. Читаем, вникаем и смотрим видео! ….о чём? Об интегралах, конечно =)

Постановка задачи уже была озвучена на указанном выше уроке, и сейчас мы быстренько актуализируем материал:

Рассмотрим интеграл . Он неберущийся. Но с другой стороны, подынтегральная функция  непрерывна на отрезке , а значит, конечная площадь существует. Как её вычислить? Приближённо. И сегодня, как вы догадываетесь – методом прямоугольников.

Разбиваем промежуток интегрирования на 5, 10, 20 или бОльшее количество равных (хотя это не обязательно) отрезков, чем больше – тем точнее будет приближение. На каждом отрезке строим прямоугольник, одна из сторон которого лежит на оси , а противоположная – пересекает график подынтегральной функции. Вычисляем площадь полученной ступенчатой фигуры, которая и будет приближённой оценкой площади  криволинейной трапеции (заштрихована на 1-м рисунке).

Очевидно, что прямоугольники можно построить многими способами, но стандартно рассматривают 3 модификации:

1) метод левых прямоугольников;
2) метод правых прямоугольников;
3) метод средних прямоугольников.

Оформим дальнейшие выкладки в рамках «полноценного» задания:

Пример 1

Вычислить определённый интеграл  приближённо:
а) методом левых прямоугольников;
б) методом правых прямоугольников.

Промежуток интегрирования разделить на  равных отрезков, результаты вычислений округлять до 0,001

Решение: признАюсь сразу, я специально выбрал такое малое значение  – из тех соображений, чтобы всё было видно на чертеже – за что пришлось поплатиться точностью приближений.

Вычислим шаг разбиения (длину каждого промежуточного отрезка):

Метод левых прямоугольников получил своё называние из-за того,

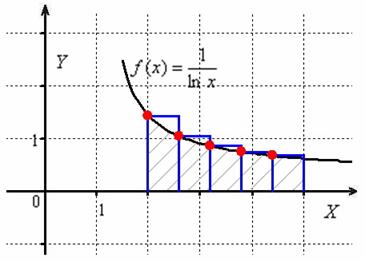
что высОты прямоугольников на промежуточных отрезках равны значениям функции в левых концах данных отрезков:

Ни в коем случае не забываем, что округление следует проводить до трёх знаков после запятой – это существенное требование условия, и «самодеятельность» здесь чревата пометкой «оформите задачу, как следует».

Вычислим площадь ступенчатой фигуры, которая равна сумме площадей прямоугольников:

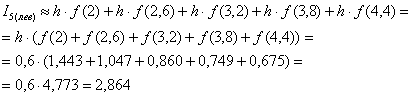
Таким образом, площадь криволинейной трапеции: . Да, приближение чудовищно грубое (завышение хорошо видно на чертеже), но и пример, повторюсь, демонстрационный. Совершенно понятно, что, рассмотрев бОльшее количество промежуточных отрезков (измельчив разбиение), ступенчатая фигура будет гораздо больше похожа на криволинейную трапецию, и мы получим лучший результат.

При использовании «правого» метода высОты прямоугольников равны значениям функции в правых концах промежуточных отрезков:

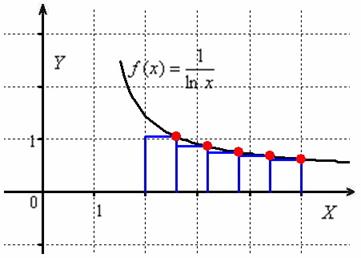
Вычислим недостающее значение  и площадь ступенчатой фигуры:

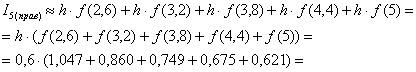
 – тут, что и следовало ожидать, приближение сильно занижено:

Запишем формулы в общем виде. Если функция  непрерывна на отрезке , и он разбит на  равных частей: , то определённый интеграл 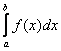 можно вычислить приближенно по формулам:
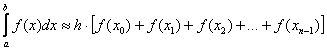 – левых прямоугольников;
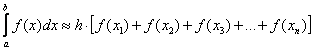 – правых прямоугольников;
(формула в следующей задаче) – средних прямоугольников,
где  – шаг разбиения.

В чём их формальное различие? В первой формуле нет слагаемого , а во второй -

На практике рассчитываемые значения  удобно заносить в таблицу:

а сами вычисления проводить в Экселе. И быстро, и без ошибок:

Если видео недоступно, смотрИте ролик здесь (Рутуб)

Ответ:

Наверное, вы уже поняли, в чём состоит метод средних прямоугольников:

Пример 2

Вычислить приближенно определенный интеграл  методом прямоугольников с точностью до 0,01. Разбиение промежутка интегрирования начать с  отрезков.

Решение: во-первых, обращаем внимание, что интеграл нужно вычислить с точностью до 0,01. Что подразумевает такая формулировка?

Если в предыдущей задаче требовалось прОсто округлить результаты до 3 знаков после запятой (а уж насколько они будут правдивы – не важно), то здесь найденное приближённое значение площади  должно отличаться от истины  не более чем на .

И во-вторых, в условии задачи не сказано, какую модификацию метода прямоугольников использовать для решения. И действительно, какую?

По умолчанию всегда используйте метод средних прямоугольников

Почему? А он при прочих равных условиях (том же самом разбиении) даёт гораздо более точное приближение. Это строго обосновано в теории, и это очень хорошо видно на чертеже:

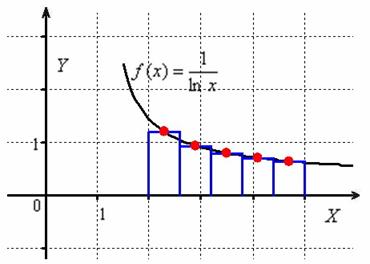
В качестве высот прямоугольников здесь принимаются значения функции, вычисленные в серединах промежуточных отрезков, и в общем виде формула приближённых вычислений запишется следующим образом:
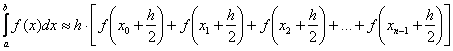, где  – шаг стандартного «равноотрезочного» разбиения .

Следует отметить, что формулу средних прямоугольников можно записать несколькими способами, но чтобы не разводить путаницу, я остановлюсь на единственном варианте, который вы видите выше.

Вычисления, как и в предыдущем примере, удобно свести в таблицу. Длина промежуточных отрезков, понятно, та же самая:  – и очевидно, что расстояние между серединами отрезков равно этому же числу. Поскольку требуемая точность вычислений составляет , то значения  нужно округлять «с запасом» – 4-5 знаками после запятой:

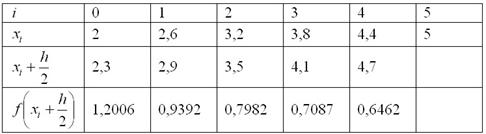
Вычислим площадь ступенчатой фигуры:

Давайте посмотрим, как автоматизировать этот процесс (копия на Рутубе):

Таким образом, по формуле средних прямоугольников:

Как оценить точность приближения? Иными словами, насколько далёк результат от истины (площади  криволинейно трапеции)? Для оценки погрешности существует специальная формула, однако, на практике её применение зачастую затруднено, и поэтому мы будем использовать «прикладной» способ:

Вычислим более точное приближение  – с удвоенным количеством отрезков разбиения: . Алгоритм решения точно такой же: .

Найдём середину первого промежуточного отрезка  и далее приплюсовываем к полученному значению по 0,3. Таблицу можно оформить «эконом-классом», но комментарий о том, что  изменяется от 0 до 10 – всё же лучше не пропускать:

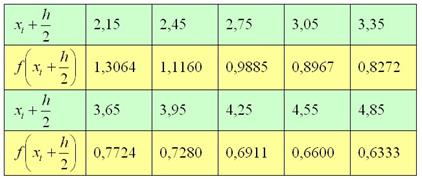
В Экселе вычисления проводятся «в один ряд» (кстати, потренируйтесь), а вот в тетради таблицу, скорее всего, придётся сделать двухэтажной (если у вас, конечно, не сверхмелкий почерк).

Вычислим суммарную площадь десяти прямоугольников:

Таким образом, более точное приближение:

Теперь находим модуль разности между двумя приближениями:

Как я уже отмечал в статье Приближённое вычисление определенных интегралов, на практике довольно часто встречается упрощённый подход: поскольку разность  больше требуемой точности , то снова удваиваем количество отрезков, находим  и разность , которая, очевидно, уже «уложится» в нашу точность: .

Однако существует более эффективный путь решения, основанный на применении правила Рунге, которое утверждает, что при использовании метода средних прямоугольников мы ошибаемся в оценке определённого интеграла менее чем на   (! для методов правых и левых прямоугольников правило использовать нельзя!).

В нашем случае: , то есть требуемая точность на самом деле достигнута, и необходимость в вычислении  отпадает.

Округляем наиболее точное приближение  до двух знаков после запятой и записываем ответ:  с точностью до 0,01

Ещё раз – что это значит? Это значит, что площадь  криволинейной трапеции гарантированно отличается от найденного приближённого значения 2,59 не более чем на 0,01.

В Примере 2 урока метод трапеций и метод Симпсона я вычислил приближённое значение этого же интеграла методом трапеций. Любознательные читатели могут сравнить полученные здесь и там результаты.

Вернемся ещё к одному маленькому нюансу, который выпал из поля зрения в самом начале урока: обязательно ли в рассматриваемом задании интеграл должен быть неберущимся? Конечно, нет. Приближённые методы вычисления прекрасно работают и для берущихся определённых интегралов. Заключительный школьный, а точнее, техникумовский пример для самостоятельного решения:

Пример 3

Вычислить интеграл  приближённо на  отрезках разбиения:

1) методом левых прямоугольников;
2) методом правых прямоугольников;
3) методом средних прямоугольников.

Вычислить более точное значение интеграла с помощью формулы Ньютона-Лейбница. Для каждого из трёх случаев найти абсолютную погрешность. Вычисления округлять до 4 знаков после запятой.

Не нужно пугаться такого развёрнутого условия – всё элементарно «перещёлкивается» в Экселе. Напоминаю, что абсолютная погрешность – это модуль разности между точным и приближённым значением. Кстати, обратите внимание на принципиальную разницу: если в предыдущих примерах речь шла лишь об оценке погрешности, то здесь нам будут известны конкретные значения этих погрешностей (т.к. интеграл берётся, и мы достоверно знаем 4 верных цифры после запятой).

Краткое решение и ответ уже, наверное, показались на вашем экране.

И, завершая эту небольшую статью, хочу отметить, что иногда метод прямоугольников ошибочно называют «плохим», «неточным» и т.п. Ничего подобного! Если уж на то пошло, его корректнее назвать «медленным» методом. Иными словами, чтобы достигнуть определённой точности – нужно рассмотреть бОльшее количество отрезков разбиения по сравнению с более эффективными методом трапеций и ещё более «быстрым» методом Симпсона.

Которые я и предлагаю вам изучить!

Пример 3: Решение: вычислим шаг разбиения:
Заполним расчётную таблицу:

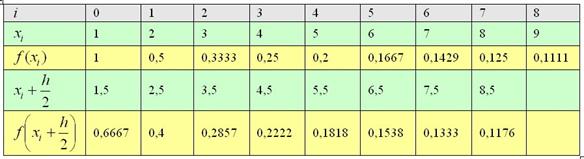
Вычислим интеграл приближённо методом:
1) левых прямоугольников:
;
2) правых прямоугольников:
;
3) средних прямоугольников:
.

Вычислим интеграл более точно по формуле Ньютона-Лейбница:

и соответствующие абсолютные погрешности вычислений:

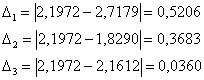
Ответ:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте