Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

24. Коэффициент ранговой корреляции Спирмена

На предыдущих уроках мы познакомились с линейным  коэффициентом корреляции Пирсона, линейной регрессией, а также потренировались в построении нелинейных моделей. Но эти методы далеко не всегда подходят для описания зависимости признака-результата  от признака-фактора . Не всегда понятна форма зависимости (Линейная? Гиперболическая? Экспоненциальная? Какая-то другая?). Эта форма бывает сложной, а то и вовсе не определИма (в принципе). И вообще, мы можем исследовать не количественный, а некоторый качественный признак.

Представьте, что в вазе лежит яблоко, киви, банан, апельсин и мандарин. Как можно проранжировать это множество? Напрашивается пронумеровать фрукты по возрастанию (либо убыванию) их массы. На первом месте самый лёгкий, на втором подобрее, на третьем – ещё добрее, … и на последнем – самый добрый:

Таким образом, каждому фрукту присвоен свой ранг (порядковый номер) по количественному критерию – массе, а именно, по возрастанию массы.

Но есть более вкусный качественный критерий. Сейчас я расположу эти фрукты в порядке моего ЛИЧНОГО вкусового предпочтения: что бы я съел в первую, вторую, третью, четвёртую и, наконец, последнюю очередь:

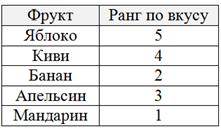
Таким образом, каждому фрукту тоже присвоен свой ранг.

И здесь любопытно сравнить качественный признак с количественным – выяснить, насколько я склонен считать лёгкие фрукты более вкусными. Для этого нужно сопоставить соответствующие ранги по фруктам и оценить степень их близости:

Иными словами, нужно определить, насколько теснА корреляционная зависимость моего вкуса от массы фрукта? Или она близка к нулю?

Но это, конечно, не самое интересное. Теперь ВЫ расположите те же фрукты в порядке СВОИХ вкусовых предпочтений. …Есть? Вероятнее всего, вы предпочли употребить фрукты в другой последовательности и проранжировали их иначе, например, так:

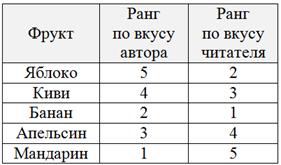
После чего появляется возможность сравнить ранги – чтобы выяснить, насколько коррелируют (совпадают) наши вкусы. Визуально можно сразу сказать, что коррелируют они слабо, т. к. читатель явно не жалует цитрусовые. Но, разумеется, есть математическая оценка этой связи, и называется она коэффициент ранговой корреляции Спирмена.

Оставим вкусное на десерт и начнём с более прозаичной задачи, где сопоставляются два количественных признака:

Пример 78

Имеются выборочные данные по  студентам:  – количество прогулов за некоторый период времени и  – суммарная успеваемость за этот период:

Найти коэффициент ранговой корреляции Спирмена, сделать вывод.

В Примере 67 мы вычислили линейный коэффициент корреляции , что говорит о сильной обратной корреляционной зависимости  – суммарной успеваемости от  – количества прогулов. Далее было найдено уравнение линейной регрессии  – это прямая, которая наилучшим образом (по сравнению с другими прямыми) приближает эмпирические точки :

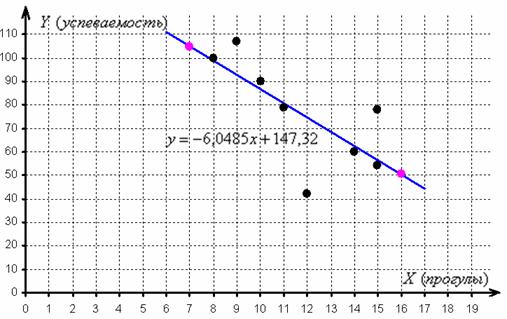
Но у такого подхода могут быть изъяны. Во-первых, прогулы и успеваемость – это величины дискретные (прерывные), но мы приблизили их непрерывной функцией (линейной). И во-вторых, зависимость может быть гораздо более сложной. Когда прогулов немного, успеваемость, вероятно, падает несущественно; когда их количество растёт – ситуация начинает ухудшаться, и, наконец, с некоторого момента достижения стремительно падают к плинтусу. Возможно, удастся подобрать кривую, удачно приближающую точки,  но у нас мало данных (8 наблюдений всего), и по чертежу сомнительно, что удастся.

Поэтому в качестве альтернативы уместно рассмотреть ранговый подход. И я расскажу вам как о ручном решении этой задачи, так и о машинном – с помощью MS Excel.

Сначала рассмотрим признак-фактор  и для удобства упорядочим количество прогулов  по возрастанию:

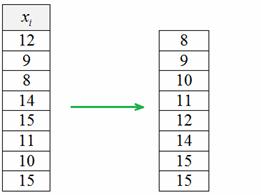
Это можно сделать на черновике или в Экселе. Теперь каждому значению  легко присвоить свой ранг  и записать ранги на чистовик, для примера парочка синих линий:

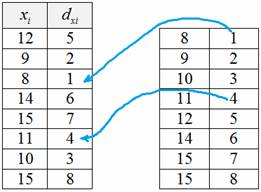
Следует заметить, что записывать числа по возрастанию (справа) вовсе не обязательно, это сделано чисто для удобства. Значения  несложно проранжировать в уме (при небольшой выборке) или опять же с помощью специальной функции Экселя (кино будет ниже).

И ещё заметим такой момент, у нас есть одинаковые значения , но ранги у них разные (7 и 8) и возникает вопрос, а почему не наоборот? В подобных ситуациях обычно находят средний арифметический ранг, который присваивают каждой варианте. В нашей задаче одинаковых значений два, поэтому их средний ранг составит:  – вот теперь всё справедливо, относим дробный ранг 7,5 и к варианте  и к варианте

Аналогично ранжируем значения  признака-результата  – тоже и ОБЯЗАЛЬНО по возрастанию значений. Ранги  легко проставить устно (что я только что сделал), без фактической сортировки «игрековых» значений:

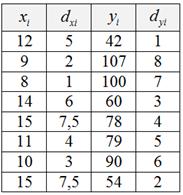
Среди значений  нет одинаковых, и поэтому ранги не нуждаются в дополнительной корректировке. После ранжирования полезно выполнить проверку. Суммы «иксовых» и «игрековых» рангов должны совпадать и равняться , в нашей задаче объём выборки составляет  и обе суммы равны .

Оценим тесноту связи между рангами. Для этого нужно вычислить коэффициент ранговой корреляции Спирмена, и это – есть в точности  линейный  коэффициент корреляции Пирсона* между рангами  и .

* а коль скоро так, то минимальный объем совокупности должен равняться 6-7.

Технически вычисления можно провести разными способами. Если вас устраивает результат «на скорую руку», то просто забиваем в Экселе:

= КОРРЕЛ(выделяем мышкой массив ;  выделяем массив ) и жмём Enter.

Но в учебных задачах, как правило, нужны подробные расчёты. Если нет дробных рангов, то коэффициент ранговой корреляции Спирмена  удобно вычислить по упрощенной формуле:

, где  – объем совокупности, а  – квадраты разностей между соответствующими рангами.

Если же дробные ранги есть (это означает, что есть одинаковые значения  и / или ), то возможны варианты. В том случае, если точность вычислений не критична и дробных рангов не так много, можно пользоваться той же формулой, но она будет давать приближённый результат: .

Но если вам необходимы абсолютно точные и подробные расчёты, то лучше расписать нахождение линейного коэффициента корреляции подробно – по образцу, только не между значениями  и , а между их рангами . Кроме того, существуют специальные модификации вышеприведённой формулы – с поправкой на повторяющиеся значения , но лишь для некоторых частных случаев. И да, должен предупредить, что формулы, приведённые во многих источниках Интернета, некорректны. Поэтому лучше потратить время и получить стопудовый результат.

В нашей задаче дробные ранги есть, и мы выберем упрощенный вариант. Для этого вычислим разности соответствующих рангов , их квадраты  и сумму . Заполним расчётную таблицу:

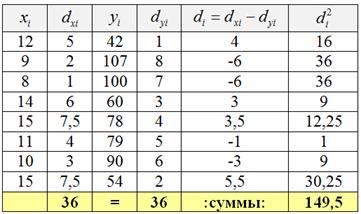
Так как среди рангов есть дробные, то формула даёт лишь приближенный результат:

Более точное значение, вычисленное с помощью функции =КОРРЕЛ() приложения MS Excel: . И, как видите, погрешность вполне приемлемая, одна сотая всего.

Поскольку  – это линейный коэффициент корреляции между рангами, то его интерпретация будет такой же.  Коэффициент ранговой корреляции изменяется в пределах  и чем он ближе по модулю к единице, тем теснее ранговая корреляционная зависимость. Для оценки тесноты связи используем ту же шкалу Чеддока:

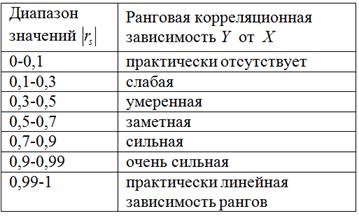
при этом если , то корреляционная связь обратная, а если , то прямая

Теперь смотрим кино, как это всё быстро подсчитать в Экселе (копия на Рутубе):

и записываем ответ:  , таким образом, существует сильная обратная корреляционная зависимость  – суммарной успеваемости от  – количества прогулов.

Напомню значение линейного коэффициента корреляции , и сейчас мы получили примерно такой же, даже более убедительный результат.

По аналогии с линейным коэффициентом, можно проверить статистическую значимость рангового коэффициента корреляции и построить соответствующие доверительные интервалы. Но это уже немного дебри статистики, с которыми можно ознакомиться, например, в учебном пособии Гмурмана (поздние издания) и других источниках. …Ловко я модернизировал метод Ивана Сусанина :)

К недостатку рангового коэффициента корреляции Спирмена можно отнести тот факт, что он практически ничего не говорит о форме зависимости.  Но повторюсь, эта форма может быть трудноопределима или не определИма вовсе. Как, например, при сопоставлении качественных признаков. По этой причине ранговый подход нашёл широчайшее применение в психологии, социологии и других гуманитарных направлениях. К слову, Чарльз Спирмен был именно психологом, и в его честь мы рассмотрим как раз простенькую задачу по психологии. На совместимость двух людей:

Пример 79

Коле и Оле было предложено проранжировать свои увлечения – от самого любимого до самого скучного / неприятного. В результате были получены следующие результаты:

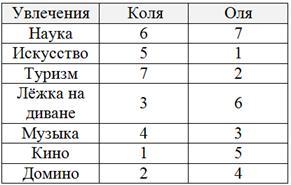
! В подобных задачах объекты принято ранжировать по убыванию их «качества»  – от самого «хорошего» до самого «плохого».

С помощью коэффициента корреляции Спирмена определить совместимость Коли и Оли в плане увлечений.

Это задача для самостоятельного решения! – все числа уже в Экселе. Образец для сверки внизу.

В наиболее благоприятном случае все ранги по увлечениям совпадают, их разности равны нулю  и посему , это говорит о практически идеальной совместимости. По мере убывания   совместимость будет падать до нейтрального околонулевого значения, где нельзя сказать, что увлечения как-то сильно совпадают или наоборот, разнятся. И в отрицательной зоне начинает нарастать негатив – вплоть до значения , при котором Коля и Оля – совершенно разные люди.

Помимо подхода Спирмена, существует и другой принцип ранжированию объектов, который выражается ранговым коэффициентом корреляции Кендалла. Но он не слишком распространен в массовой практике (по крайне мере, технической), поэтому едем дальше:

Коэффициент корреляции Фехнера

Решения и ответы:

Пример 79. Решение: вычислим разности соответствующих рангов , их квадраты  и сумму :

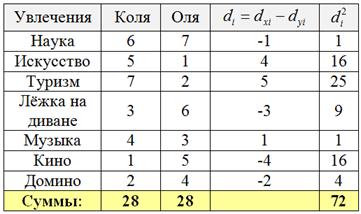
Так как среди рангов нет дробных, то:
 

Ответ: , таким образом, Коля и Оля имеют слабо-умеренно-негативную совместимость по интересам.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте