


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как исследовать функцию и построить её график?
Похоже, я начинаю понимать одухотворённо-проникновенный лик вождя мирового пролетариата, автора собрания сочинений в 55 томах… Нескорый путь начался элементарными сведениями о функциях и графиках, и вот сейчас работа над трудоёмкой темой заканчивается закономерным результатом – статьёй о полном исследовании функции. Долгожданное задание формулируется следующим образом:
исследовать функцию методами дифференциального исчисления и на основании результатов исследования построить её график
Или короче: исследовать функцию и построить график.
Зачем исследовать? В простых случаях нас не затруднит разобраться с элементарными функциями, начертить график, полученный с помощью элементарных геометрических преобразований и т. п. Однако свойства и графические изображения более сложных функций далеко не очевидны, именно поэтому и необходимо целое исследование.
Основные этапы решения сведены в справочном материале Схема исследования функции, это ваш путеводитель по разделу. Чайникам требуется пошаговое объяснение темы, некоторые читатели не знают с чего начать и как организовать исследование, а продвинутым студентам, возможно, будут интересны лишь некоторые моменты. Но кем бы вы ни были, уважаемый посетитель, предложенный конспект с указателями на различные уроки в кратчайший срок сориентирует и направит Вас в интересующем направлении. Роботы отдыхают =) Руководство свёрстано в виде pdf-файла и доступно по ссылке выше, и, конечно, оно заняло заслуженное место в нашей Справочной.
Исследование функции обычно разбивают на 5-7 пунктов, а-ка:
1) Область определения, непрерывность, четность / нечётность, периодичность функции.
3) Нули функции, интервалы знакопостоянства.
4) Возрастание, убывание и экстремумы функции.
5) Выпуклость, вогнутость и перегибы графика.
6) Дополнительные точки и график по результатам исследования.
На счёт заключительного действия, думаю, всем всё понятно – будет очень обидно, если в считанные секунды его перечеркнут и вернут задание на доработку. ПРАВИЛЬНЫЙ И АККУРАТНЫЙ ЧЕРТЁЖ – это основной результат решения! Он с большой вероятностью «прикроет» аналитические оплошности, в то время как некорректный и / или небрежный график доставит проблемы даже при идеально проведённом исследовании.
Следует отметить, что в других источниках количество пунктов исследования, порядок их выполнения и стиль оформления могут существенно отличаться от предложенной мной схемы, но в большинстве случаев её вполне достаточно. Простейшая версия задачи состоит всего из 2-3 этапов и формулируется примерно так: «исследовать функцию с помощью производной и построить график» либо «исследовать функцию с помощью 1-й и 2-й производной, построить график».
Естественно – если в вашей методичке подробно разобран другой алгоритм или ваш преподаватель строго требует придерживаться его лекций, то придётся внести некоторые коррективы в решение. Не сложнее, чем заменить вилку бензопилой ложкой.
Итак, вооружившись общей схемой исследования, где рассмотрена структура и техника выполнения задачи, переходим к изучению стратегии и тактики действий. Успешно прошедшим курс обучения откроется тайна числа 69 ;-) С нетерпением скрипим колёсиком мыши =)
Пример 1
Исследовать функцию и по результатам исследования построить график.
![]()
Решение:
1) Функция определена и непрерывна на всей числовой прямой: ![]() . Это очень хорошо, отпадают вертикальные асимптоты.
. Это очень хорошо, отпадают вертикальные асимптоты.
Проверим функцию на чётность/нечётность:
![]()
После чего следует шаблонная отписка:
![]() , значит, данная функция не является чётной или нечётной.
, значит, данная функция не является чётной или нечётной.
Очевидно, что функция непериодическая.
2) Асимптоты, поведение функции на бесконечности.
Так как функция непрерывна на ![]() , то вертикальные асимптоты отсутствуют.
, то вертикальные асимптоты отсутствуют.
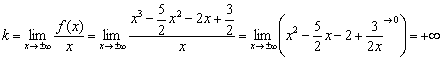
Следовательно, нет и наклонных асимптот.
Примечание: напоминаю, что ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() , поэтому итоговый предел равен именно «плюс» бесконечности.
, поэтому итоговый предел равен именно «плюс» бесконечности.
Выясним, как ведёт себя функция на бесконечности:
![]()
Иными словами, если идём вправо, то график уходит бесконечно далеко вверх, если влево – бесконечно далеко вниз. Да, здесь тоже два предела под единой записью. Если у вас возникло недопонимание знака ![]() , посетите урок о бесконечно малых функциях.
, посетите урок о бесконечно малых функциях.
Таким образом, функция не ограничена сверху и не ограничена снизу. Учитывая, что у нас нет точек разрыва, становится понятна и область значений функции: ![]() – тоже любое действительное число.
– тоже любое действительное число.
ПОЛЕЗНЫЙ ТЕХНИЧЕСКИЙ ПРИЁМ
Каждый этап задания приносит новую информацию о графике функции, поэтому в ходе решения удобно использовать своеобразный МАКЕТ. Изобразим на черновике декартову систему координат. Что уже точно известно? Во-первых, у графика нет асимптот, следовательно, прямые чертить не нужно. Во-вторых, мы знаем, как функция ведёт себя на бесконечности. Согласно проведённому анализу, нарисуем первое приближение:
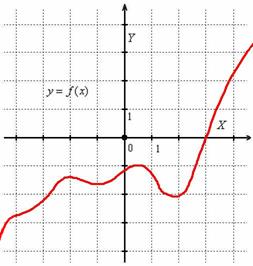
Заметьте, что в силу непрерывности функции на ![]() и того факта, что
и того факта, что ![]() , график должен, по меньшей мере, один раз пересечь ось
, график должен, по меньшей мере, один раз пересечь ось ![]() . ...А может быть точек пересечения несколько?
. ...А может быть точек пересечения несколько?
3) Нули функции и интервалы знакопостоянства.
Сначала найдём точку пересечения графика с осью ординат. Для этого нужно просто вычислить значение функции при ![]() :
:
![]()
Полтора над уровнем моря.
Чтобы найти точки пересечения с осью ![]() (нули функции) требуется решить уравнение
(нули функции) требуется решить уравнение ![]() , и тут нас поджидает неприятный сюрприз:
, и тут нас поджидает неприятный сюрприз:
![]()
В конце притаился свободный член, который существенно затрудняет задачу.
Такое уравнение имеет, как минимум, один действительный корень, и чаще всего этот корень иррационален. В худшей же сказке нас поджидают три поросёнка. Уравнение разрешимо с помощью так называемых формул Кардано, но расход времени и бумаги сопоставим чуть ли не со всем исследованием. В этой связи разумнее устно либо на черновике попытаться подобрать хотя бы один целый корень. Проверим, не являются ли оными числа ![]() :
:
![]() – не подходит;
– не подходит;
![]() – есть!
– есть!
Здесь повезло. В случае неудачи можно протестировать ещё ![]() и
и ![]() , а если и эти числа не подошли, то шансов на выгодное решение уравнения, боюсь, очень мало. Тогда пункт исследования лучше полностью пропустить – авось станет что-нибудь понятнее на завершающем шаге, когда будут «пробиваться» дополнительные точки. И если-таки корень (корни) явно «нехорошие», то об интервалах знакопостоянства лучше вообще скромно умолчать да поаккуратнее выполнить чертёж.
, а если и эти числа не подошли, то шансов на выгодное решение уравнения, боюсь, очень мало. Тогда пункт исследования лучше полностью пропустить – авось станет что-нибудь понятнее на завершающем шаге, когда будут «пробиваться» дополнительные точки. И если-таки корень (корни) явно «нехорошие», то об интервалах знакопостоянства лучше вообще скромно умолчать да поаккуратнее выполнить чертёж.
Однако у нас есть красивый корень ![]() , поэтому делим многочлен
, поэтому делим многочлен ![]() на
на ![]() без остатка:
без остатка:
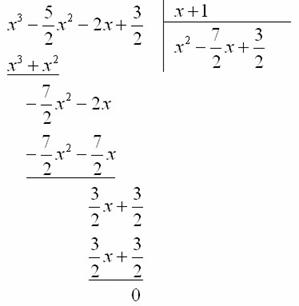
Алгоритм деления многочлена на многочлен детально разобран в первом примере урока Сложные пределы.
В итоге левая часть исходного уравнения ![]() раскладывается в произведение:
раскладывается в произведение:
![]()
А теперь немного о здоровом образе жизни. Я, конечно же, понимаю, что квадратные уравнения полезно решать каждый день, но сегодня сделаем исключение: уравнение ![]() имеет два действительных корня
имеет два действительных корня ![]() .
.
На числовой прямой отложим найденные значения ![]() и методом интервалов определим знаки функции:
и методом интервалов определим знаки функции:

Таким образом, на интервалах ![]() график расположен
график расположен
ниже оси абсцисс ![]() , а на интервалах
, а на интервалах ![]() – выше данной оси
– выше данной оси ![]() .
.
Полученные выводы позволяют детализировать наш макет, и второе приближение графика выглядит следующим образом:
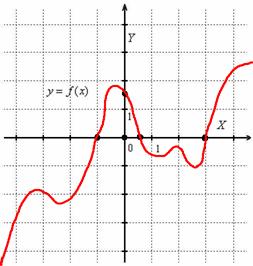
Обратите внимание, что на интервале ![]() функция обязательно должна иметь хотя бы один максимум, а на интервале
функция обязательно должна иметь хотя бы один максимум, а на интервале ![]() – хотя бы один минимум. Но сколько раз, где и когда будет «петлять» график, мы пока не знаем. К слову, функция может иметь и бесконечно много экстремумов.
– хотя бы один минимум. Но сколько раз, где и когда будет «петлять» график, мы пока не знаем. К слову, функция может иметь и бесконечно много экстремумов.
4) Возрастание, убывание и экстремумы функции.
Найдём критические точки:
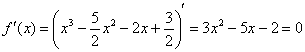
Данное уравнение имеет два действительных корня ![]() . Отложим их на числовой прямой и определим знаки производной:
. Отложим их на числовой прямой и определим знаки производной:

Следовательно, функция возрастает на ![]() и убывает на
и убывает на ![]() .
.
В точке ![]() функция достигает максимума:
функция достигает максимума: ![]() .
.
В точке ![]() функция достигает минимума:
функция достигает минимума: ![]() .
.
Установленные факты загоняют наш шаблон в довольно жёсткие рамки:
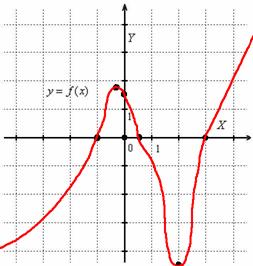
Что и говорить, дифференциальное исчисление – штука мощная. Давайте окончательно разберёмся с формой графика:
5) Выпуклость, вогнутость и точки перегиба.
Найдём критические точки второй производной:
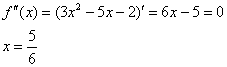
Определим знаки ![]() :
:

График функции является выпуклым на ![]() и вогнутым на
и вогнутым на ![]() . Вычислим ординату точки перегиба:
. Вычислим ординату точки перегиба: ![]() .
.
Практически всё прояснилось.
6) Осталось найти дополнительные точки, которые помогут точнее построить график, и выполнить самопроверку. В данном случае их немного, но пренебрегать не будем:

Выполним чертёж:
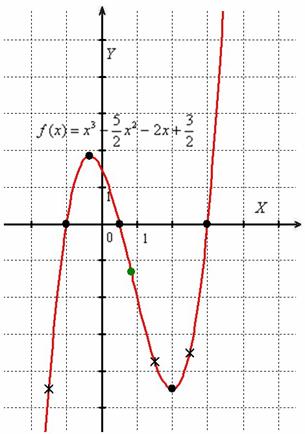
Зелёным цветом отмечена точка перегиба, крестиками – дополнительные точки. График кубической функции симметричен относительно своей точки перегиба, которая всегда расположена строго посередине между максимумом и минимумом.
По ходу выполнения задания я привёл три гипотетических промежуточных чертежа. На практике же достаточно нарисовать систему координат, отмечать найденные точки и после каждого пункта исследования мысленно прикидывать, как может выглядеть график функции. Студентам с хорошим уровнем подготовки не составит труда провести такой анализ исключительно в уме без привлечения черновика.
Для самостоятельного решения:
Пример 2
Исследовать функцию и построить график.
![]()
Тут всё быстрее и веселее, примерный образец чистового оформления в конце урока.
Немало секретов раскрывает исследование дробно-рациональных функций:
Пример 3
Методами дифференциального исчисления исследовать функцию и на основании результатов исследования построить её график.
![]()
Решение: первый этап исследования не отличается чем-то примечательным, за исключением дырки в области определения:
1) Функция определена и непрерывна на всей числовой прямой кроме точки ![]() , область определения:
, область определения: ![]() .
.
![]()
![]() , значит, данная функция не является четной или нечетной.
, значит, данная функция не является четной или нечетной.
Очевидно, что функция непериодическая.
График функции представляет собой две непрерывные ветви, расположенные в левой и правой полуплоскости – это, пожалуй, самый важный вывод 1-го пункта.
2) Асимптоты, поведение функции на бесконечности.
а) С помощью односторонних пределов исследуем поведение функции вблизи подозрительной точки, где явно должна быть вертикальная асимптота:
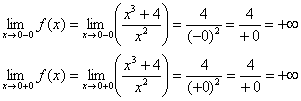
Действительно, функции терпит бесконечный разрыв в точке ![]() ,
,
а прямая ![]() (ось
(ось ![]() ) является вертикальной асимптотой графика
) является вертикальной асимптотой графика ![]() .
.
б) Проверим, существуют ли наклонные асимптоты:
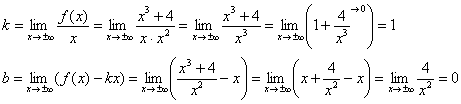
Да, прямая ![]() является наклонной асимптотой графика
является наклонной асимптотой графика ![]() при
при ![]() .
.
Пределы ![]() анализировать смысла не имеет, поскольку и так понятно, что функция в обнимку со своей наклонной асимптотой не ограничена сверху и не ограничена снизу.
анализировать смысла не имеет, поскольку и так понятно, что функция в обнимку со своей наклонной асимптотой не ограничена сверху и не ограничена снизу.
Второй пункт исследования принёс много важной информации о функции. Выполним черновой набросок:
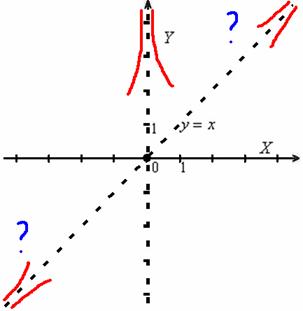
Вывод № 1 касается интервалов знакопостоянства. На «минус» бесконечностиграфик функции однозначно расположен ниже оси абсцисс, а на «плюс» бесконечности – выше данной оси. Кроме того, односторонние пределы сообщили нам, что и слева и справа от точки ![]() функция тоже больше нуля. Обратите внимание, что в левой полуплоскости график, по меньшей мере, один раз обязан пересечь ось абсцисс. В правой полуплоскости нулей функции может и не быть.
функция тоже больше нуля. Обратите внимание, что в левой полуплоскости график, по меньшей мере, один раз обязан пересечь ось абсцисс. В правой полуплоскости нулей функции может и не быть.
Вывод № 2 состоит в том, что функция возрастает на ![]() и слева от точки
и слева от точки ![]() (идёт «снизу вверх»). Справа же от данной точки – функция убывает (идёт «сверху вниз»). У правой ветви графика непременно должен быть хотя бы один минимум. Слева экстремумы не гарантированы.
(идёт «снизу вверх»). Справа же от данной точки – функция убывает (идёт «сверху вниз»). У правой ветви графика непременно должен быть хотя бы один минимум. Слева экстремумы не гарантированы.
Вывод № 3 даёт достоверную информацию о вогнутости графика в окрестности точки ![]() . О выпуклости / вогнутости на бесконечностях мы пока ничего сказать не можем, поскольку линия может прижиматься к своей асимптоте как сверху, так и снизу. Вообще говоря, есть аналитический способ выяснить это прямо сейчас, но форма графика «даром» прояснится на более поздних этапах.
. О выпуклости / вогнутости на бесконечностях мы пока ничего сказать не можем, поскольку линия может прижиматься к своей асимптоте как сверху, так и снизу. Вообще говоря, есть аналитический способ выяснить это прямо сейчас, но форма графика «даром» прояснится на более поздних этапах.
Зачем было это «занудство»? Чтобы контролировать последующие пункты исследования и не допустить ошибок! Дальнейшие выкладки не должны противоречить сделанным выводам.
3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График функции не пересекает ось ![]() .
.
С осью ![]()
Методом интервалов определим знаки ![]() :
:

![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
Результаты пункта полностью соответствуют Выводу № 1. После каждого этапа смотрИте на черновик, мысленно сверяйтесь с исследованием и дорисовывайте график функции.
4) Возрастание, убывание, экстремумы функции.
В рассматриваемом примере числитель почленно делится на знаменатель, что очень выгодно для дифференцирования:
![]()
Собственно, это уже проделывалось при нахождении асимптот.
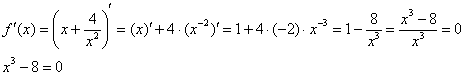
![]() – критическая точка.
– критическая точка.
Определим знаки ![]() :
:

![]() возрастает на
возрастает на ![]() и убывает на
и убывает на ![]()
В точке ![]() функция достигает минимума:
функция достигает минимума: ![]() .
.
Разночтений с Выводом № 2 также не обнаружилось, и, вероятнее всего, мы на правильном пути.
5) Выпуклость, вогнутость, перегибы графика.
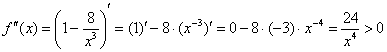 , значит, график функции является вогнутым на всей области определения.
, значит, график функции является вогнутым на всей области определения.
Отлично – и чертить ничего не надо.
Точки перегиба отсутствуют.
Вогнутость согласуется с Выводом № 3, более того, указывает, что на бесконечности (и там и там) график функции расположен выше своей наклонной асимптоты.
6) Добросовестно приколотим задание дополнительными точками. Вот здесь придётся изрядно потрудиться, поскольку из исследования нам известны только две точки.

И картинка, которую, наверное, многие давно представили:
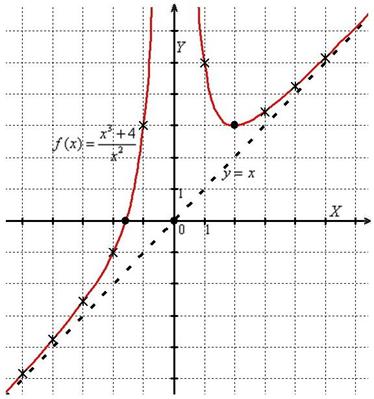
В ходе выполнения задания нужно тщательно следить за тем, чтобы не возникало противоречий между этапами исследования, но иногда ситуация бывает экстренной или даже отчаянно-тупиковой. Вот «не сходится» аналитика – и всё тут. В этом случае рекомендую аварийный приём: находим как можно больше точек, принадлежащих графику (сколько хватит терпения), и отмечаем их на координатной плоскости. Графический анализ найденных значений в большинстве случаев подскажет, где правда, а где ложь. Кроме того, график можно предварительно построить с помощью какой-нибудь программы, например, в том же Экселе (понятно, для этого нужны навыки).
Пример 4
Методами дифференциального исчисления исследовать функцию и построить её график.
![]()
Это пример для самостоятельного решения. В нём самоконтроль усиливается чётностью функции – график симметричен относительно оси ![]() , и если в вашем исследовании что-то противоречит данному факту, ищите ошибку.
, и если в вашем исследовании что-то противоречит данному факту, ищите ошибку.
Чётную или нечётную функцию можно исследовать только при ![]() , а потом пользоваться симметрией графика. Такое решение оптимально, однако выглядит, по моему мнению, весьма непривычно. Лично я рассматриваю всю числовую ось, но дополнительные точки нахожу всё же лишь справа:
, а потом пользоваться симметрией графика. Такое решение оптимально, однако выглядит, по моему мнению, весьма непривычно. Лично я рассматриваю всю числовую ось, но дополнительные точки нахожу всё же лишь справа:
Пример 5
Провести полное исследование функции и построить её график.
![]()
Решение: понеслась нелёгкая:
1) Функция определена и непрерывна на всей числовой прямой: ![]() .
.
![]() , значит, данная функция является нечетной, её график симметричен относительно начала координат.
, значит, данная функция является нечетной, её график симметричен относительно начала координат.
Очевидно, что функция непериодическая.
2) Асимптоты, поведение функции на бесконечности.
Так как функция непрерывна на ![]() , то вертикальные асимптоты отсутствуют
, то вертикальные асимптоты отсутствуют
Для функции, содержащей экспоненту, типично раздельное исследование «плюс» и «минус» бесконечности, однако нашу жизнь облегчает как раз симметрия графика – либо и слева и справа есть асимптота, либо её нет. Поэтому оба бесконечных предела можно оформить под единой записью. В ходе решения используем правило Лопиталя:
![]()
Прямая ![]() (ось
(ось ![]() ) является горизонтальной асимптотой графика при
) является горизонтальной асимптотой графика при ![]() .
.
Обратите внимание, как я хитро избежал полного алгоритма нахождения наклонной асимптоты: предел ![]() вполне легален и проясняет поведение функции на бесконечности, а горизонтальная асимптота обнаружилась «как бы заодно».
вполне легален и проясняет поведение функции на бесконечности, а горизонтальная асимптота обнаружилась «как бы заодно».
Из непрерывности на ![]() и существования горизонтальной асимптоты следует тот факт, что функция ограничена сверху и ограничена снизу.
и существования горизонтальной асимптоты следует тот факт, что функция ограничена сверху и ограничена снизу.
3) Точки пересечения графика с координатными осями, интервалы знакопостоянства.
Здесь тоже сокращаем решение:
график ![]() проходит через начало координат.
проходит через начало координат.
Других точек пересечения с координатными осями нет. Более того, интервалы знакопостоянства очевидны, и ось можно не чертить: ![]() , а значит, знак функции зависит только от «икса»:
, а значит, знак функции зависит только от «икса»:
![]() , если
, если ![]() ;
;
![]() , если
, если ![]() .
.
! Настоятельно рекомендую оформлять черновой шаблон графика
по ходу исследования!
4) Возрастание, убывание, экстремумы функции.

![]() – критические точки.
– критические точки.
Точки симметричны относительно нуля, как оно и должно быть.
Определим знаки производной:

Функция возрастает на интервале ![]() и убывает на интервалах
и убывает на интервалах ![]() .
.
В точке ![]() функция достигает максимума:
функция достигает максимума: ![]() .
.
В силу свойства ![]() (нечётности функции) минимум можно не вычислять:
(нечётности функции) минимум можно не вычислять:
![]()
Поскольку функция убывает на интервале ![]() , то, очевидно, на «минус» бесконечности график расположен под своей асимптотой. На интервале
, то, очевидно, на «минус» бесконечности график расположен под своей асимптотой. На интервале ![]() функция тоже убывает, но здесь всё наоборот – после перехода через точку максимума
функция тоже убывает, но здесь всё наоборот – после перехода через точку максимума ![]() линия приближается к оси
линия приближается к оси ![]() уже сверху.
уже сверху.
Из вышесказанного также следует, что график функции является выпуклым на «минус» бесконечности и вогнутым на «плюс» бесконечности.
После этого пункта исследования прорисовалась и область значений функции:
![]()
Если у вас возникло недопонимание каких-либо моментов, ещё раз призываю начертить в тетради координатные оси и с карандашом в руках заново проанализировать каждый вывод задания.
5) Выпуклость, вогнутость, перегибы графика.

![]() – критические точки.
– критические точки.
Симметрия точек сохраняется, и, скорее всего, мы не ошибаемся.
Определим знаки ![]() :
:

График функции является выпуклым на 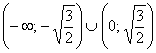 и вогнутым на
и вогнутым на 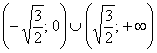 .
.
Выпуклость / вогнутость на крайних интервалах подтвердилась.
Во всех критических точках существуют перегибы графика. Найдём ординаты точек перегиба, при этом снова сократим количество вычислений, используя нечётность функции:
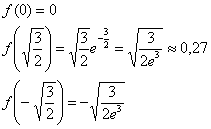
6) Дополнительные точки целесообразно рассчитать только для правой полуплоскости:
![]()
Выполним чертёж:
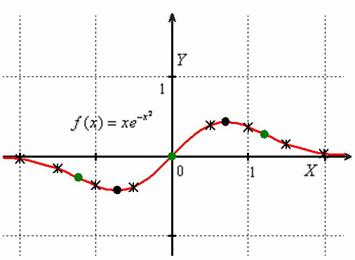
Такой вот симпатяга….
Изначально было запланировано 5 примеров, и если честно, я ожидал, что статья получится заметно больше по объему. Конечно, хочется исследовать ещё одну функцию, но с другой стороны – нельзя объять необъятное, поэтому сегодня воздержимся от логарифмов. Самое важное – усвоить методы, приёмы и хитрости исследования, которые мы только что разобрали.
Желающие могут пройти на страницу готовых задач по высшей математике и закачать архив, который содержит 69 исследований. Выбирайте любую функцию и тренируйтесь! И, кто знает…, может встретите ту единственную, которую так давно искали =)
Приятного времяпровождения!
Решения и ответы:
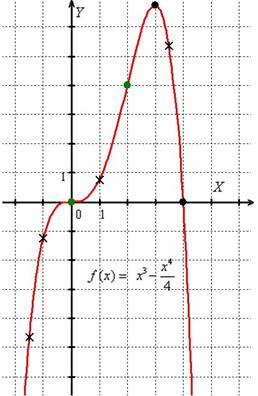
Пример 2. Решение: проведём исследование функции:
1) Функция определена и непрерывна на всей числовой прямой, ![]() .
.
![]()
![]() , значит, данная функция не является четной или нечетной.
, значит, данная функция не является четной или нечетной.
Функция непериодическая.
2) Асимптоты графика, поведение функции на бесконечности.
Так как функция непрерывна на ![]() , то вертикальные асимптоты отсутствуют.
, то вертикальные асимптоты отсутствуют.
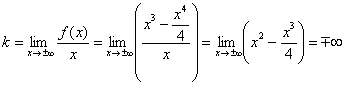 , значит, наклонные асимптоты также отсутствуют.
, значит, наклонные асимптоты также отсутствуют.
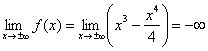 , функция не ограничена снизу.
, функция не ограничена снизу.
3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График ![]() проходит через начало координат.
проходит через начало координат.
С осью ![]()
![]()
Определим знаки ![]() :
:

![]() , если
, если ![]() ,
,
![]() , если
, если ![]() .
.
4) Возрастание, убывание, экстремумы функции.
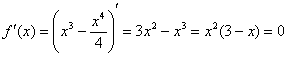
![]() – критические точки.
– критические точки.
Определим знаки ![]() :
:

![]() возрастает на
возрастает на ![]() и убывает на
и убывает на ![]() .
.
В точке ![]() функция достигает максимума:
функция достигает максимума: ![]()
5) Выпуклость, вогнутость, перегибы графика.
![]()
![]() – критические точки.
– критические точки.
Определим знаки ![]() :
:

График функции является выпуклым на ![]() и вогнутым на
и вогнутым на ![]() .
.
В обеих критических точках существуют перегибы графика.
![]()
6) Найдем дополнительные точки:
![]()
Выполним чертёж:
Пример 4. Решение: проведем исследование функции:
1) Функция определена и непрерывна на всей числовой прямой, ![]() .
.
![]()
![]() , значит, данная функция является четной, ее график симметричен относительно оси ординат.
, значит, данная функция является четной, ее график симметричен относительно оси ординат.
Очевидно, что функция непериодическая.
2) Асимптоты, поведение функции на бесконечности.
Так как функция непрерывна на всей числовой прямой, то вертикальные асимптоты отсутствуют.
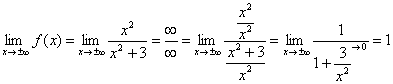
Прямая ![]() является горизонтальной асимптотой для графика
является горизонтальной асимптотой для графика ![]() при
при ![]() .
.
3) Точки пересечения графика с координатными осями, интервалы знакопостоянства функции.
График функции проходит через начало координат.
![]() на всей области определения.
на всей области определения.
4) Возрастание, убывание, экстремумы функции.
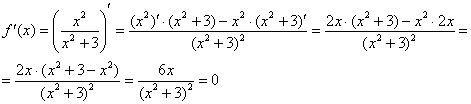
![]() – критическая точка.
– критическая точка.
Определим знаки ![]() :
:

![]() возрастает на
возрастает на ![]() и убывает на
и убывает на ![]() .
.
В точке ![]() функция достигает минимума:
функция достигает минимума: ![]() .
.
5) Выпуклость, вогнутость, перегибы графика.
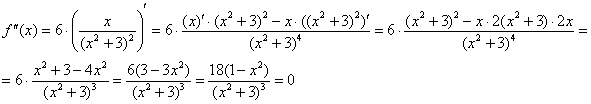
![]() – критические точки.
– критические точки.
Определим знаки ![]() :
:

График ![]() является выпуклым на
является выпуклым на ![]() и вогнутым на
и вогнутым на ![]() .
.
В обеих критических точках существуют перегибы графика: ![]() .
.
6) Найдем дополнительные точки и выполним чертёж:

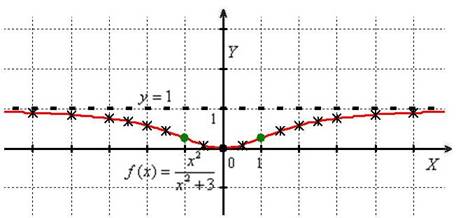
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright