


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Интегрирование корней (иррациональных функций).
Примеры решений
Вот и пробил час интегралов, которые вас заждались!
Интегралы с корнями (радикалами) мы уже решали, и этот урок будет посвящён тем случаям, когда изученные приёмы не срабатывают. Как правило, в таких примерах корни находятся в загадочном положении, и зачастую их несколько штук. А посему интегрирование иррациональных функций лучше изучать уже при некоторых знаниях и навыках решения неопределённого интеграла, поскольку многие из них – самые настоящие крепкие орешки. Таким образом, если Вы чайник, и за плечами всего десяток прорешанных интегралов, да и с методом замены переменной в неопределенном интеграле не очень, то лучше начать со статьи Неопределенный интеграл. Примеры решений. Хотя, не пугаемся, не разбегаемся – простейшие примеры с квадратными корнями, думаю, будут понятны широкому кругу студентов. Весь материал я постараюсь изложить максимально подробно и максимально доступно.
Сначала мы разберём простые случаи, затем чуть более громоздкие (с разными корнями), и закончится повествование биномиальными интегралами, кои уже являются немного дебрями интегралов, где преподаватель-волк частенько кушает зайцев.
Итак, прошу любить и жаловать первый параграф
Интегралы от корней. Типовые методы и приемы решения
Вспоминаем счастливые школьные годы. Пыонеры на уроках математики, приступая к изучению корней, в первую очередь знакомятся с квадратным корнем. Мы пойдем тем же путём.
Пример 1
Найти неопределенный интеграл
![]()
Анализируя подынтегральную функцию, приходишь к печальному выводу, что она совсем не напоминает табличные интегралы. Вот если бы всё это добро находилось в числителе – было бы просто. Или бы корня внизу не было. Или двучлена. Никакие методы интегрирования дробей тоже не помогают. Что делать?
Основной приём решения иррациональных интегралов – это замена переменной, которая избавит нас от ВСЕХ корней в подынтегральной функции.
В нашем примере корень всего один и напрашивается его прямая замена ![]() . Мысль верная! При этом удобно сразу возвести обе части в квадрат и использовать модифицированный вариант
. Мысль верная! При этом удобно сразу возвести обе части в квадрат и использовать модифицированный вариант ![]() , где
, где ![]() (т. к. корень чётный). В результате подстановки
(т. к. корень чётный). В результате подстановки ![]() – корень пропадает (модуль не нужен, ибо «тэ» положительно).
– корень пропадает (модуль не нужен, ибо «тэ» положительно).
Если бы в подынтегральной функции вместо квадратного корня у нас находился ![]() , то мы бы провели замену
, то мы бы провели замену ![]() . Если бы там был
. Если бы там был ![]() – то
– то ![]() , и так далее. Обращаю внимание, что при чётном корне
, и так далее. Обращаю внимание, что при чётном корне ![]() , а при нечётном – «тэ» в общем случае может быть любого знака, и при чистовом оформлении примеров я буду подразумевать это по умолчанию.
, а при нечётном – «тэ» в общем случае может быть любого знака, и при чистовом оформлении примеров я буду подразумевать это по умолчанию.
Хорошо, ![]() у нас превратится в
у нас превратится в ![]() . Что произойдет с двучленом
. Что произойдет с двучленом ![]() ? Сложностей нет: если
? Сложностей нет: если ![]() , то
, то ![]() .
.
Осталось выяснить, во что превратится дифференциал ![]() . Делается это так.
. Делается это так.
Берём нашу замен в виде ![]() и навешиваем дифференциалы на обе части:
и навешиваем дифференциалы на обе части:
![]()
(распишу максимально подробно)
![]()
![]()
Как видите, замена получилась своеобразной, и её техническое оформление отличается от «классического» способа, который мы рассмотрели на уроке Метод замены переменной в неопределенном интеграле.
Чистовое оформление решения должно выглядеть примерно так:
![]()
Проведём замену ![]() , следовательно:
, следовательно: ![]()

(1) Проводим подстановку после замены (как, что и куда, уже рассмотрено).
(2) Выносим константу за пределы интеграла. Числитель и знаменатель сокращаем на ![]() .
.
(3) Получившийся интеграл является табличным, готовим его для интегрирования, выделяя квадрат
(4) Интегрируем по таблице, используя формулу ![]() .
.
(5) Проводим обратную замену. Как это делается? Вспоминаем, от чего плясали: если ![]() , то
, то ![]() .
.
Внимание! Для изучения дальнейших примеров нужно владеть материалом первого параграфа урока Интегрирование некоторых дробей.
Пример 2
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Как-то так получилось, что в Примерах 1, 2 «голый» числитель с одиноким дифференциалом ![]() . Что же. Исправим ситуацию.
. Что же. Исправим ситуацию.
Пример 3
Найти неопределенный интеграл
![]()
Предварительный анализ подынтегральной функции опять показывает, что лёгкого пути нет. А поэтому нужно избавляться от корня.
![]()
Как и в предыдущих примерах, корень здесь один, и за «тэ» мы обозначаем ВЕСЬ корень:
![]() , возводим обе части в квадрат
, возводим обе части в квадрат ![]() и навешиваем дифференциалы:
и навешиваем дифференциалы:
![]()
![]()
![]()
С числителем разобрались. Что делать с двучленом в знаменателе?
Берем нашу замену ![]() и выражаем из неё:
и выражаем из неё: ![]()
Если ![]() , то
, то ![]()
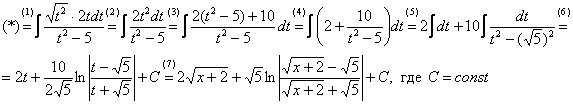
(1) Проводим подстановку в соответствии с выполненной заменой.
(2) Причёсываем числитель. Константу здесь я предпочел не выносить за знак интеграла (можно делать и так, ошибкой не будет)
(3) Раскладываем числитель в сумму. Ещё раз настоятельно рекомендую ознакомиться с первым параграфом урока Интегрирование некоторых дробей. Канители с разложением числителя в сумму в иррациональных интегралах будет предостаточно, очень важно отработать это прием.
(4) Почленно делим числитель на знаменатель.
(5) Используем свойстово линейности неопределенного интеграла. Во втором интеграле выделяем квадрат ![]() для последующего интегрирования по таблице.
для последующего интегрирования по таблице.
(6) Интегрируем по таблице. Первый интеграл совсем простой, во втором используем табличную формулу высокого логарифма ![]() .
.
(7) Проводим обратную замену. Если изначально ![]() , то, обратно:
, то, обратно: ![]()
Пример 4
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения, если вы невнимательно проработали предыдущие примеры, то допустите ошибку! Полное решение и ответ в конце урока.
Принципиально так же решаются интегралы с несколькими одинаковыми корнями, например ![]() ,
, ![]() и т. д. А что делать, если в подынтегральной функции корни разные?
и т. д. А что делать, если в подынтегральной функции корни разные?
Пример 5
Найти неопределенный интеграл
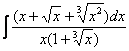
Вот и пришла расплата за голые числители. Когда встречается такой интеграл, обычно становится страшно. Но страхи напрасны, после проведения подходящей замены подынтегральная функция упрощается. Задача состоит в следующем: провести удачную замену, чтобы сразу избавиться от ВСЕХ корней.
Когда даны разные корни удобно придерживаться следующей схемы решения. Сначала выписываем на черновике подынтегральную функцию, при этом все корни представляем в виде ![]() :
: 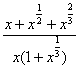 . Нас будут интересовать знаменатели степеней:
. Нас будут интересовать знаменатели степеней:
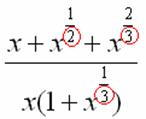
Записываем эти знаменатели: 2, 3, 3.
Теперь нужно найти наименьшее общее кратное чисел 2, 3, 3 – такое натуральное число, чтобы оно делилось и на 2 и на 3 (в данном случае), кроме того, это число должно быть как можно меньше.
Очевидно, что наименьшим общим кратным является число 6. Оно делится и на 2 и на 3 и, кроме того, меньше шестёрки в этом смысле ничего нет.
Как многие уже догадались, замена в данном интеграле будет следующей: ![]() , при этом удобнее использовать модифицированный вариант, возведя обе части в 6-ю степень:
, при этом удобнее использовать модифицированный вариант, возведя обе части в 6-ю степень: ![]() и имея в виду, что
и имея в виду, что ![]() (т. к. корень чётный).
(т. к. корень чётный).
Оформляем решение:
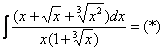
Проведем замену ![]() и соответствующую подстановку:
и соответствующую подстановку: ![]()

(1) Записываем интеграл с новой переменной, согласно замене.
(2) Избавляемся от корней. Выносим константу за знак интеграла. Сокращаем числитель и знаменатель на ![]() .
.
(3) Сокращаем числитель и знаменатель еще на ![]() .
.
(4) Раскладываем числитель в сумму (как это сделать, уже неоднократно упоминалось).
(5) Почленно делим числитель на знаменатель.
(6) Интегрируем по таблице. При этом константу я снова «прилепил» к каждому из трех слагаемых (можно этого и не делать, момент несущественный).
(7) Проводим обратную замену. Если ![]() , то, обратно:
, то, обратно: ![]() . В ходе обратной замены некоторые корни лучше сразу сократить (обычно это делается устно). В рассмотренном примере сокращение корней встретилось в первом слагаемом:
. В ходе обратной замены некоторые корни лучше сразу сократить (обычно это делается устно). В рассмотренном примере сокращение корней встретилось в первом слагаемом: ![]()
Как видите, особых сложностей нет, несмотря на то, что сначала интеграл показался трудным и страшным.
Пример 6
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения.
Интегрирование биномиальных интегралов
Или если говорить строже, это интеграл от биномиального дифференциала:
![]() с рациональными степенями «эм», «эн» и «пэ», и сразу исключим тривиальные случаи
с рациональными степенями «эм», «эн» и «пэ», и сразу исключим тривиальные случаи ![]() и иже с ними. Ну и, разумеется, действительные коэффициенты «а» и «бэ» не равны нулю.
и иже с ними. Ну и, разумеется, действительные коэффициенты «а» и «бэ» не равны нулю.
Такой интеграл берётся в трёх случаях
1) Случай первый. Самый лёгкий. Если степень ![]() – целое число.
– целое число.
Например: ![]()
Представим интеграл в стандартном виде, это можно делать как на черновике, так и на чистовике:
![]()
Мы видим, что степень ![]() – целая, а, значит, действительно имеет место первый случай. На самом деле биномиальный интеграл первого типа решается практически так же, как интегралы в Примерах 5, 6, поэтому приводить почти такие же решения особого смысла нет – я просто покажу, какую замену здесь нужно провести.
– целая, а, значит, действительно имеет место первый случай. На самом деле биномиальный интеграл первого типа решается практически так же, как интегралы в Примерах 5, 6, поэтому приводить почти такие же решения особого смысла нет – я просто покажу, какую замену здесь нужно провести.
Смотрим на знаменатели дробей:
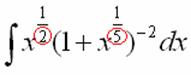
Записываем знаменатели: 2, 5. Находим наименьшее общее кратное этих чисел. Очевидно, это 10: оно делится и на 2 и на 5, кроме того – десятка самая маленькая в этом смысле.
После замены ![]() и подстановки
и подстановки ![]() все корни гарантировано пропадут. Повторюсь, примеров для первого случая не будет, так как они очень похожи на недавно разобранные интегралы.
все корни гарантировано пропадут. Повторюсь, примеров для первого случая не будет, так как они очень похожи на недавно разобранные интегралы.
2) Случай второй
![]()
Если ![]() – целое число, то нужно провести подстановку
– целое число, то нужно провести подстановку ![]() , где
, где ![]() – знаменатель дроби
– знаменатель дроби ![]() .
.
Спокойствие, только спокойствие, сейчас во всём разберемся.
Пример 7
Найти неопределенный интеграл
![]()
Представим интеграл в стандартном виде ![]() :
:
![]() . Вообще говоря, формально правильнее было записать
. Вообще говоря, формально правильнее было записать ![]() , но перестановка слагаемых в скобках не играет никакой роли.
, но перестановка слагаемых в скобках не играет никакой роли.
Выписываем степени:
![]() ,
, ![]() ,
, ![]()
Сразу проверяем, не относится ли наш интеграл к первому случаю?
![]() – целое? Нет.
– целое? Нет.
Проверяем второй случай:
![]() – целое, значит у нас второй случай
– целое, значит у нас второй случай
Согласно правилу для второго случая, нужно провести подстановку ![]() , где
, где ![]() – знаменатель дроби
– знаменатель дроби ![]() . В рассматриваемом примере
. В рассматриваемом примере ![]() , и знаменатель этой дроби равен «двойке». Таким образом, чтобы гарантировано избавиться от корня, используем конструкцию
, и знаменатель этой дроби равен «двойке». Таким образом, чтобы гарантировано избавиться от корня, используем конструкцию ![]() . Обращаю внимание, что на самом деле здесь мы меняем корень
. Обращаю внимание, что на самом деле здесь мы меняем корень ![]() , и я рекомендую придерживаться следующего алгоритма, оформляем решение:
, и я рекомендую придерживаться следующего алгоритма, оформляем решение:
![]()
Проведём замену ![]() , обе части которой возведём в квадрат:
, обе части которой возведём в квадрат: ![]() ..
..
Теперь нужно выяснить, во что превратится оставшаяся часть подынтегрального выражения ![]()
Берём ![]() и навешиваем дифференциалы на обе части:
и навешиваем дифференциалы на обе части:
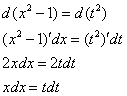
Но вот, незадача, у нас ![]() , а нам нужно выразить
, а нам нужно выразить ![]() .
.
Умножаем обе части на ![]() :
:
![]()
Таким образом: ![]() . Уже лучше, но хотелось бы выразить
. Уже лучше, но хотелось бы выразить ![]() только через
только через ![]() , а в правой части
, а в правой части ![]() – «икс» в квадрате внизу. Что делать? Вспоминаем нашу замену в виде
– «икс» в квадрате внизу. Что делать? Вспоминаем нашу замену в виде ![]() и выражаем из неё нужный нам
и выражаем из неё нужный нам ![]() .
.
Окончательно: ![]() . Головоломно, но, увы, другие алгоритмы еще запутаннее.
. Головоломно, но, увы, другие алгоритмы еще запутаннее.
Собственно, всё готово, продолжаем решение:
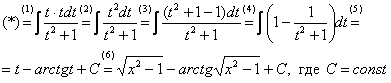
(1) Проводим подстановку согласно замене.
(2) Записываем компактно числитель.
(3) Раскладываем знаменатель в сумму.
(4) Почленно делим числитель на знаменатель.
(5) Интегрируем по таблице.
(6) Проводим обратную замену: если ![]() , то
, то ![]()
Пример 8
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
3) Случай третий. Самый сложный
![]()
Если ![]() – целое число, то нужно провести подстановку
– целое число, то нужно провести подстановку ![]() , где
, где ![]() – знаменатель дроби
– знаменатель дроби ![]() .
.
Пример 9
Найти неопределенный интеграл
![]()
Представим интеграл в стандартном виде ![]() :
:
![]() .
.
Выписываем степени и не помешает, кстати, и коэффициенты:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
1) Не относится ли наш интеграл к первому случаю?
![]() – целое? Нет.
– целое? Нет.
2) Проверяем второй случай:
![]() – целое? Нет.
– целое? Нет.
3) ![]() – целое! Значит, у нас третий случай.
– целое! Значит, у нас третий случай.
Согласно правилу для третьего случая, нужно провести подстановку ![]() , где
, где ![]() – знаменатель дроби
– знаменатель дроби ![]() . В рассматриваемом примере
. В рассматриваемом примере ![]() , и знаменатель этой дроби равен опять же «двойке». Коэффициенты (будьте внимательны)
, и знаменатель этой дроби равен опять же «двойке». Коэффициенты (будьте внимательны) ![]() ,
, ![]()
Таким образом, от корня гарантировано избавляет ![]() .
.
Оформляем решение:
![]()
Проведем замену в виде ![]() .
.
Разбираемся с корнем. Это труднее, чем в предыдущих случаях.
Сначала из нашей «заготовки» ![]() нужно выразить «икс квадрат»:
нужно выразить «икс квадрат»:
![]()
Теперь подставляем ![]() под корень:
под корень:
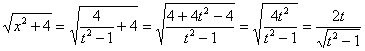 , обращаю ваше внимание, что вверху после извлечения корня модуль при «тэ» не нужен (не останавливаясь вновь на подробностях).
, обращаю ваше внимание, что вверху после извлечения корня модуль при «тэ» не нужен (не останавливаясь вновь на подробностях).
На втором этапе выясняем, во что превратится оставшаяся часть подынтегрального выражения ![]() . Берем нашу «заготовку»
. Берем нашу «заготовку» ![]() и навешиваем дифференциалы на обе части:
и навешиваем дифференциалы на обе части:
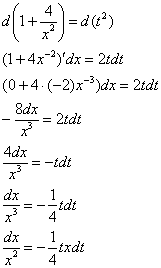
Опять проблема, в правой части у нас есть «икс», а нам нужно всё выразить через «тэ».
Берем ранее найденное выражение ![]() и выражаем
и выражаем ![]()
Окончательно:
![]()
В итоге мы выразили через «тэ» и ![]() и
и ![]() , и всё готово для продолжения решения:
, и всё готово для продолжения решения:

(1) Меняем корень и оставшуюся часть подынтегрального выражения.
(2) Упрощаем потроха.
(3) Меняем знак в знаменателе и выносим минус за пределы интеграла (можно было не делать, но так удобнее).
(4) Проводим обратную замену. В третьем случае биномиального интеграла это тоже труднее. Если изначально было ![]() , то
, то ![]() .
.
(5) Избавляемся от четырехэтажности в логарифме.
Пример 10
Найти неопределенный интеграл
![]()
Да что такое, опять числитель голый… Честное слово, не нарочно получилось =)
Это пример для самостоятельного решения. Подсказка: здесь ![]()
Полное решение и ответ только для выживших студентов.
Что делать, если биномиальный интеграл ![]() не подходит ни под один из рассмотренных трех случаев? Это грустный четвертый случай. Такой интеграл является неберущимся.
не подходит ни под один из рассмотренных трех случаев? Это грустный четвертый случай. Такой интеграл является неберущимся.
Почти всё рассмотрено. Есть другие разновидности интегралов с корнями, например, когда корень является аргументом какой-либо функции. Или под корнем находится дробь. Найти такие примеры можно на странице Сложные интегралы.
Желаю успехов!
Решения и ответы:
Пример 2. Решение:
![]()
Проведем замену ![]() ,
, ![]()
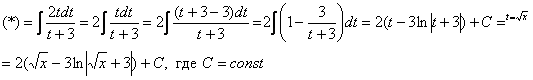
Пример 4. Решение:
![]()
Проведём замену кубического корня, то бишь : ![]() . Навешиваем дифференциалы на обе части:
. Навешиваем дифференциалы на обе части:
![]()
![]()
![]()
Вот почему дифференциалы нужно именно НАВЕШИВАТЬ на обе части и добросовестно раскрывать эти дифференциалы. Немало чайников здесь формально напишет ![]() и допустит ошибку.
и допустит ошибку.

Пример 6. Решение:
![]()
Подстановка: ![]()

Примечание: на самом деле данное решение не совсем рационально. Перед тем, как раскладывать числитель в сумму, лучше было поменять у знаменателя знак и сразу вынести минус за пределы интеграла: ![]() – в таком виде подбирать числитель значительно проще.
– в таком виде подбирать числитель значительно проще.
Пример 8. Решение:
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
1) ![]() – целое? Нет.
– целое? Нет.
2) ![]() – целое, значит у нас второй случай.
– целое, значит у нас второй случай.
Проведём замену в виде ![]() , фактически меняем корень:
, фактически меняем корень: ![]() .
.
![]()
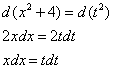
![]()
![]()
Если ![]() , то
, то ![]()
Окончательно: ![]()
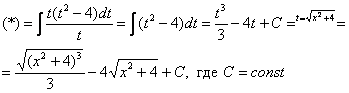
Пример 10. Решение:
![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
1) ![]() – целое? Нет.
– целое? Нет.
2) ![]() – целое? Нет.
– целое? Нет.
3) ![]() – целое!
– целое!
Замена в виде ![]() , в данном случае:
, в данном случае:
![]()
Разбираемся с корнем. Из ![]() :
:
![]()
Тогда:
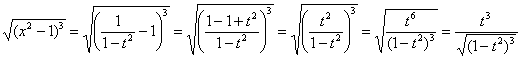
Оставшаяся часть подынтегрального выражения: ![]()
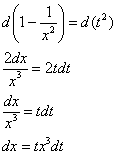
Чему равно ![]() ?
?
![]()
Окончательно:
![]()
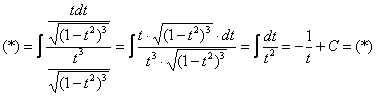
Обратная замена. Если ![]() , то
, то ![]()
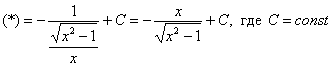
Вы выполнили проверку, может, где ошибочка вышла ;)
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright