


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Производные сложных функций нескольких переменных
Возможно, название этой статьи вас озадачит. И в самом деле – ведь на предыдущих уроках (Частные производные функции двух и трёх переменных) мы уже неоднократно сталкивались с частными производными сложных функций наподобие ![]() и более трудными примерами. Так о чём же ещё можно рассказать?! …А всё как в жизни – нет такой сложности, которую было бы нельзя усложнить =) Но математика – на то и математика, чтобы укладывать многообразие нашего мира в строгие рамки. И иногда это удаётся сделать одним-единственным предложением:
и более трудными примерами. Так о чём же ещё можно рассказать?! …А всё как в жизни – нет такой сложности, которую было бы нельзя усложнить =) Но математика – на то и математика, чтобы укладывать многообразие нашего мира в строгие рамки. И иногда это удаётся сделать одним-единственным предложением:
В общем случае сложная функция имеет вид ![]() , где, по меньшей мере, одна из букв
, где, по меньшей мере, одна из букв ![]() представляет собой функцию, которая может зависеть от произвольного количества переменных.
представляет собой функцию, которая может зависеть от произвольного количества переменных.
Минимальный и самый простой вариант – это давно знакомая сложная функция ![]() одной переменной, производную которой мы научились находить в прошлом семестре. Навыками дифференцирования функций
одной переменной, производную которой мы научились находить в прошлом семестре. Навыками дифференцирования функций ![]() вы тоже обладаете (взгляните на те же функции
вы тоже обладаете (взгляните на те же функции ![]() ).
).
Таким образом, сейчас нас будет интересовать как раз случай ![]() . По причине великого разнообразия сложных функций общие формулы их производных имеют весьма громоздкий и плохо усваиваемый вид. В этой связи я ограничусь конкретными примерами, из которых вы сможете понять общий принцип нахождения этих производных:
. По причине великого разнообразия сложных функций общие формулы их производных имеют весьма громоздкий и плохо усваиваемый вид. В этой связи я ограничусь конкретными примерами, из которых вы сможете понять общий принцип нахождения этих производных:
Пример 1
Дана сложная функция ![]() , где
, где ![]() . Требуется:
. Требуется:
1) найти её производную и записать полный дифференциал 1-го порядка;
2) вычислить значение производной при ![]() .
.
Решение: во-первых, разберёмся с самой функцией. Нам предложена функция, зависящая от ![]() и
и ![]() , которые в свою очередь являются функциями одной переменной:
, которые в свою очередь являются функциями одной переменной:
![]()
Во-вторых, обратим пристальное внимание на само задание – от нас требуется найти производнУЮ, то есть, речь идёт вовсе не о частных производных ![]() , которые мы привыкли находить! Так как функция
, которые мы привыкли находить! Так как функция ![]() фактически зависит только от одной переменной, то под словом «производная» подразумевается полная производная
фактически зависит только от одной переменной, то под словом «производная» подразумевается полная производная ![]() . Как её найти?
. Как её найти?
Первое, что приходит на ум, это прямая подстановка и дальнейшее дифференцирование. Подставим ![]() в функцию
в функцию ![]() :
:
![]() , после чего с искомой производной никаких проблем:
, после чего с искомой производной никаких проблем:
![]()
И, соответственно, полный дифференциал: ![]()
Это решение математически корректно, но маленький нюанс состоит в том, что когда задача формулируется так, как она сформулирована – такого варварства от вас никто не ожидает =) А если серьёзно, то придраться тут действительно можно. Представьте, что функция ![]() описывает полёт шмеля, а вложенные функции
описывает полёт шмеля, а вложенные функции ![]() меняются в зависимости от температуры. Выполняя прямую подстановку
меняются в зависимости от температуры. Выполняя прямую подстановку ![]() , мы получаем лишь частную информацию
, мы получаем лишь частную информацию ![]() , которая характеризует полёт, скажем, только в жаркую погоду. Более того, если человеку не сведущему в шмелях предъявить готовый результат
, которая характеризует полёт, скажем, только в жаркую погоду. Более того, если человеку не сведущему в шмелях предъявить готовый результат ![]() и даже сказать, что это за функция, то он так ничего и не узнает о фундаментальном законе
и даже сказать, что это за функция, то он так ничего и не узнает о фундаментальном законе ![]() полёта!
полёта!
Вот так вот совершенно неожиданно брат наш жужжащий помог осознать смысл и важность универсальной формулы:
![]()
Привыкайте к «двухэтажным» обозначениям производных – в рассматриваемом задании в ходу именно они. При этом следует быть очень аккуратным в записи: производные с прямыми значками «дэ» – это полные производные, а производные с округлыми значками ![]() – это частные производные. С последних и начнём:
– это частные производные. С последних и начнём:
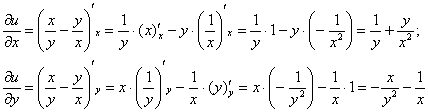
Ну а с «хвостами» вообще всё элементарно:
![]()
Подставим найденные производные в нашу формулу:
![]()
Когда функция изначально предложена в замысловатом виде, то будет логичным (и тому дано объяснение выше!) оставить в таком же виде и результаты:
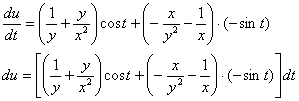
При этом в «навороченных» ответах лучше воздержаться даже от минимальных упрощений (тут, например, напрашивается убрать 3 минуса) – и вам работы меньше, и мохнатый друг доволен рецензировать задание проще.
Однако не лишней будет черновая проверка. Подставим ![]() в найденную производную и проведём упрощения:
в найденную производную и проведём упрощения:
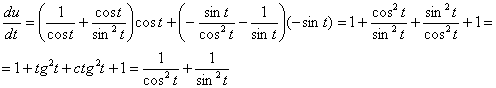
(на последнем шаге использованы тригонометрические формулы ![]() ,
, ![]() )
)
В результате получен тот же результат, что и при «варварском» методе решения.
Вычислим производную в точке ![]() . Сначала удобно выяснить «транзитные» значения (значения функций
. Сначала удобно выяснить «транзитные» значения (значения функций ![]() ):
):
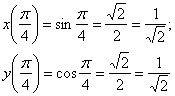
Теперь оформляем итоговые расчёты, которые в данном случае можно выполнить по-разному. Использую интересный приём, в котором 3 и 4 «этажа» упрощаются не по обычным правилам, а преобразуются как частное двух чисел:
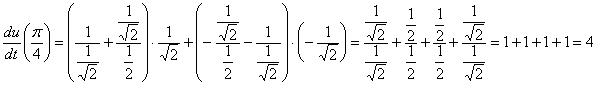
И, конечно же, грех не проверить по более компактной записи ![]() :
:
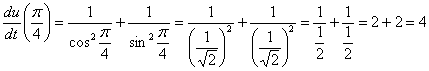
Ответ:
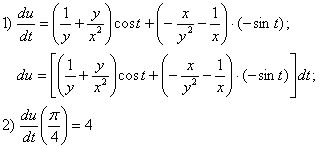
Бывает, что задача предлагается в «полуобщем» виде:
«Найти производную функции ![]() , где
, где ![]() »
»
То есть «главная» функция не дана, но её «вкладыши» вполне конкретны. Ответ следует дать в таком же стиле:
![]()
Более того, условие могут немного подшифровать:
«Найти производную функции ![]() »
»
В этом случае нужно самостоятельно обозначить вложенные функции какими-нибудь подходящими буквами, например, через ![]() и воспользоваться той же формулой:
и воспользоваться той же формулой:
![]()
К слову, о буквенных обозначениях. Я уже неоднократно призывал не «цепляться за буквы», как за спасательный круг, и сейчас это особенно актуально! Анализируя различные источники по теме, у меня вообще сложилось впечатление, что авторы «пошли вразнос» и стали безжалостно бросать студентов в бурные пучины математики =) Так что уж простите:))
Пример 2
Найти производную ![]() функции
функции ![]() , если
, если ![]()
Другие обозначения не должны приводить в замешательство! Каждый раз, когда вы встречаете подобное задание, нужно ответить на два простых вопроса:
1) От чего зависит «главная» функция? В данном случае функция «зет» зависит от двух функций («у» и «вэ»).
2) От каких переменных зависят вложенные функции? В данном случае оба «вкладыша» зависят только от «икса».
Таким образом, у вас не должно возникнуть трудностей, чтобы адаптировать формулу к этой задаче!
Краткое решение и ответ в конце урока.
Дополнительные примеры по первому виду можно найти в задачнике Рябушко (ИДЗ 10.1), ну а мы берём курс на функцию трёх переменных:
Пример 3
Дана функция ![]() , где
, где ![]() .
.
Вычислить производную в точке ![]()
Формула производной сложной функции ![]() , как многие догадываются, имеет родственный вид:
, как многие догадываются, имеет родственный вид:
![]()
Решайте, раз догадались =)
На всякий случай приведу и общую формулу для функции ![]() :
:
![]() , хотя на практике вы вряд ли встретите что-то длиннее Примера 3.
, хотя на практике вы вряд ли встретите что-то длиннее Примера 3.
Кроме того, иногда приходится дифференцировать «урезанный» вариант – как правило, функцию вида ![]() либо
либо ![]() . Оставляю вам этот вопрос для самостоятельного исследования – придумайте какую-нибудь простенькие примеры, подумайте, поэкспериментируйте и выведите укороченные формулы производных.
. Оставляю вам этот вопрос для самостоятельного исследования – придумайте какую-нибудь простенькие примеры, подумайте, поэкспериментируйте и выведите укороченные формулы производных.
Если что-то осталось недопонятым, пожалуйста, неторопливо перечитайте и осмыслите первую часть урока, поскольку сейчас задача усложнится:
Пример 4
Найти частные производные сложной функции ![]() , где
, где ![]()
Решение: данная функция имеет вид ![]() , и после прямой подстановки
, и после прямой подстановки ![]() и
и ![]() мы получаем привычную функцию двух переменных:
мы получаем привычную функцию двух переменных:
![]()
Но такой страх не то чтобы не принято, а уже и не хочется дифференцировать =) Поэтому воспользуемся готовыми формулами. Чтобы вы быстрее уловили закономерность, я выполню некоторые пометки:
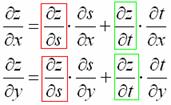
Внимательно просмотрите картинку сверху вниз и слева направо….
Сначала найдём частные производные «главной» функции:
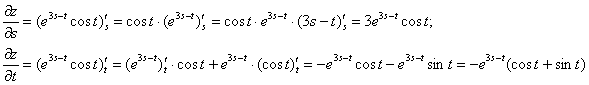
Теперь находим «иксовые» производные «вкладышей»:
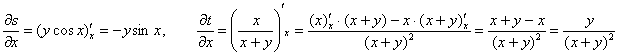
и записываем итоговую «иксовую» производную:
![]()
Аналогично с «игреком»:
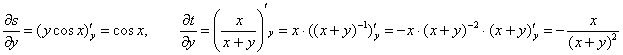
и
![]()
Можно придерживаться и другого стиля – сразу найти все «хвосты» ![]() и потом записать обе производные.
и потом записать обе производные.
Ответ:
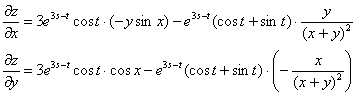
О подстановке ![]() что-то как-то совсем не думается =) =), а вот причесать результаты немножко можно. Хотя, опять же, зачем? – только усложните проверку преподавателю.
что-то как-то совсем не думается =) =), а вот причесать результаты немножко можно. Хотя, опять же, зачем? – только усложните проверку преподавателю.
Если потребуется, то полный дифференциал тут записывается по обычной формуле, и, кстати, как раз на данном шаге становится уместной лёгкая косметика:
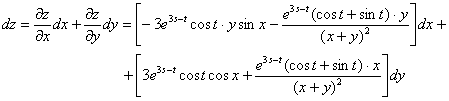
Такой вот... ....гроб на колёсиках.
Ввиду популярности рассматриваемой разновидности сложной функции пара заданий для самостоятельного решения. Более простой пример в «полуобщем» виде – на понимание самой формулы ;-):
Пример 5
Найти частные производные функции ![]() , где
, где ![]()
И посложнее – с подключением техники дифференцирования:
Пример 6
Найти полный дифференциал функции ![]() , где
, где ![]()
Нет, я вовсе не пытаюсь «отправить вас на дно» – все примеры взяты из реальных работ, и «в открытом море» вам могут попасться какие угодно буквы. В любом случае потребуется проанализировать функцию (ответив на 2 вопроса – см. выше), представить её в общем виде и аккуратно модифицировать формулы частных производных. Возможно, сейчас немного попутаетесь, но зато поймёте сам принцип их конструирования! Ибо настоящие задачи только начинаются :)))
Шутка.
Пример 7
Найти частные производные и составить полный дифференциал сложной функции
![]() , где
, где ![]()
Решение: «главная» функция имеет вид ![]() и по-прежнему зависит от двух переменных – «икса» и «игрека». Но по сравнению с Примером 4, добавилась ещё одна вложенная функция, и поэтому формулы частных производных тоже удлиняются. Как и в том примере, для лучшего вИдения закономерности, я выделю «главные» частные производные различными цветами:
и по-прежнему зависит от двух переменных – «икса» и «игрека». Но по сравнению с Примером 4, добавилась ещё одна вложенная функция, и поэтому формулы частных производных тоже удлиняются. Как и в том примере, для лучшего вИдения закономерности, я выделю «главные» частные производные различными цветами:
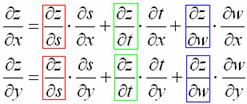
И снова – внимательно изучите запись сверху вниз и слева направо.
Так как задача сформулирована в «полуобщем» виде, то все наши труды, по существу, ограничиваются нахождением частных производных вложенных функций:
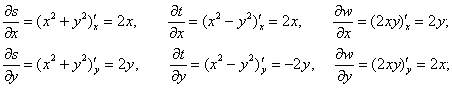
Справится первоклассник:
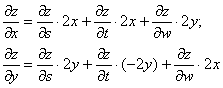
И даже полный дифференциал получился вполне себе симпатичный:
![]()
Я специально не стал предлагать вам какую-то конкретную функцию ![]() – чтобы лишние нагромождения не помешали хорошо разобраться в принципиальной схеме задачи.
– чтобы лишние нагромождения не помешали хорошо разобраться в принципиальной схеме задачи.
Ответ:
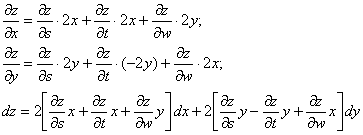
Довольно часто можно встретить «разнокалиберные» вложения, например:
![]()
Здесь «главная» функция хоть и имеет вид ![]() , но всё равно зависит и от «икс», и от «игрек». Поэтому работают те же самые формулы – просто некоторые частные производные будут равны нулю. Причём, это справедливо и для функций вроде
, но всё равно зависит и от «икс», и от «игрек». Поэтому работают те же самые формулы – просто некоторые частные производные будут равны нулю. Причём, это справедливо и для функций вроде ![]() , у которых каждый «вкладыш» зависит от какой-то одной переменной.
, у которых каждый «вкладыш» зависит от какой-то одной переменной.
Похожая ситуация имеет место и в двух заключительных примерах урока:
Пример 8
Найти полный дифференциал сложной функции ![]() в точке
в точке ![]()
Решение: условие сформулировано «бюджетным» образом, и мы должны сами обозначить вложенные функции. По-моему, неплохой вариант:
![]()
Во «вкладышах» присутствуют (ВНИМАНИЕ!) ТРИ буквы – старые-добрые «икс-игрек-зет», а значит, «главная» функция ![]() фактически зависит от трёх переменных. Её можно формально переписать в виде
фактически зависит от трёх переменных. Её можно формально переписать в виде ![]() , и частные производные в этом случае определяются следующими формулами:
, и частные производные в этом случае определяются следующими формулами:
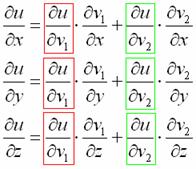
Сканируем, вникаем, улавливаем….
В нашей задаче:
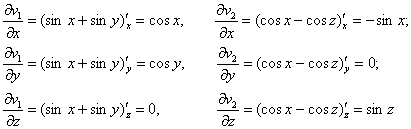
Таким образом:
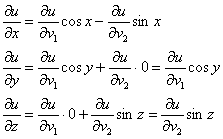
Теперь вспоминаем формулу полного дифференциала функции трёх переменных. Полный дифференциал в точке ![]() имеет вид
имеет вид ![]() .
.
Вычислим частные производные в данной точке:
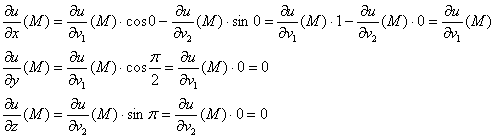
Следует отметить, что слово «вычислить» здесь прозвучало в известной степени условно, поскольку нам не известна ни «главная» функция ![]() ни её производные. Но символически всё отражено! Так, например, запись
ни её производные. Но символически всё отражено! Так, например, запись ![]() означает, что мы подставили координаты точки «эм» в производную
означает, что мы подставили координаты точки «эм» в производную ![]() и получили некоторое число.
и получили некоторое число.
Искомый дифференциал в точке:
![]()
Концовку решения можно оформить и другим способом – сначала записать полный дифференциал в общем виде:
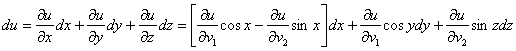
и только на последнем шаге подставить координаты точки ![]() в нужные места:
в нужные места:
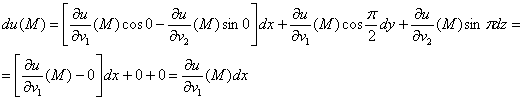
Ответ: ![]()
Вот и всё! А показалось, наверное, поначалу чем-то невообразимо страшным. …Я чувствую, вам понравилось =). Для самостоятельного решения:
Пример 9
Найти полный дифференциал сложной функции ![]() в точке
в точке ![]()
На том, пожалуй, и завершим. Функции бОльшей размерности лично мне не встречались, но если вам таки доведётся столкнуться с «олимпиадным» примером, то, думаю, многие без особого труда распишут и более забористые производные, благо, принцип их нахождения прослеживается очень чётко.
Желаю успехов!
Решения и ответы:
Пример 2: Решение: используем формулу ![]() .
.
В данном случае:
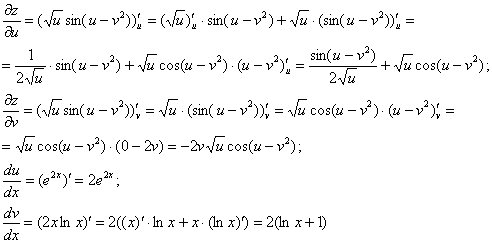
Ответ: 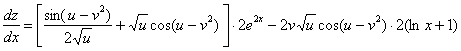
Пример 3: Решение: используем формулу ![]()
В данной задаче:
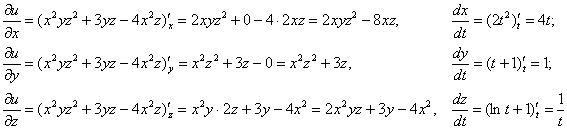
Таким образом:
![]()
Вычислим производную при ![]() :
:
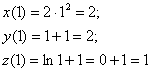
В результате:
![]()
Ответ: ![]()
Пример 5: Решение: используем формулы:
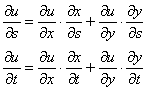
В данном случае:
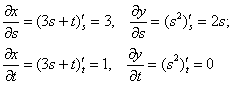
Ответ: ![]()
Пример 6: Решение: сначала найдём частные производные 1-го порядка:
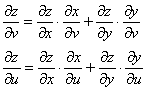
В данной задаче:
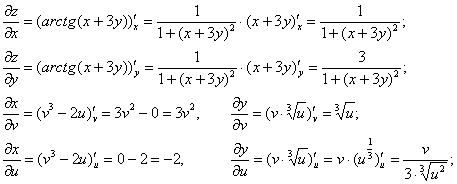
Таким образом:
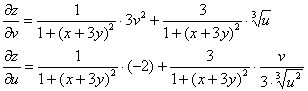
Составим полный дифференциал:
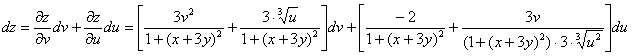
Ответ: 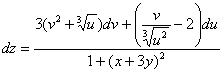
Пример 9: Решение: обозначим ![]()
Найдём частные производные 1-го порядка:
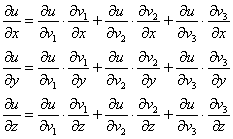
В данном случае:
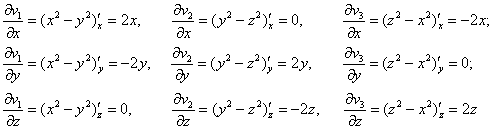
Таким образом:
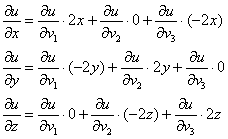
Составим полный дифференциал 1-го порядка:
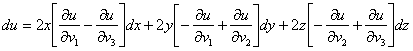
Найдём полный дифференциал в точке ![]() :
:
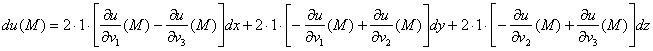
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright