


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Дифференциальные уравнения, допускающие понижение порядка
Кроме распространенных однородных и неоднородных уравнений второго порядка и высших порядков с постоянными коэффициентами, рядовому студенту часто приходится сталкиваться с другим достаточно обширным классом диффуров: дифференциальными уравнениями, допускающими понижение порядка.
Различают три основных типа таких уравнений, которые мы последовательно рассмотрим на данном уроке. По какому принципу решаются данные уравнения? Старо, как второй том матана – уравнения, допускающие понижение порядка, в конечном итоге сводятся к дифференциальным уравнениям первого порядка и интегрируются с помощью методов, которые вы уже должны знать из моих статей.
Люди собрались опытные, большие, поэтому не будем проводить разминку с перекидыванием резинового мячика из рук в руки, а сразу перейдем к делу. Но и чайники тоже могут присоединиться, я не выгоняю за дверь, а ставлю ссылки на темы, по которым у вас есть пробелы.
Метод повторного интегрирования правой части
Рассмотрим дифференциальное уравнение вида ![]() , где
, где ![]() – производная «энного» порядка, а правая часть
– производная «энного» порядка, а правая часть ![]() зависит только от «икс». В простейшем случае
зависит только от «икс». В простейшем случае ![]() может быть константой.
может быть константой.
Данное дифференциальное уравнение решается последовательным интегрированием правой части. Причём интегрировать придется ровно ![]() раз.
раз.
На практике наиболее популярной разновидность является уравнение второго порядка: ![]() . Дважды интегрируем правую часть и получаем общее решение. Уравнение третьего порядка
. Дважды интегрируем правую часть и получаем общее решение. Уравнение третьего порядка ![]() необходимо проинтегрировать трижды, и т. д. Но диффуров четвертого и более высоких порядков в практических заданиях что-то даже и не припомню.
необходимо проинтегрировать трижды, и т. д. Но диффуров четвертого и более высоких порядков в практических заданиях что-то даже и не припомню.
Пример 1
Найти общее решение дифференциального уравнения
![]()
Решение: данное дифференциальное уравнение имеет вид ![]() .
.
Понижаем степень уравнения до первого порядка:
![]()
Или короче: ![]() , где
, где ![]() – константа
– константа
Теперь интегрируем правую часть еще раз, получая общее решение:
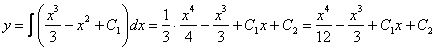
Ответ: общее решение: ![]()
Проверить общее решение такого уравнения обычно очень легко. В данном случае нужно лишь найти вторую производную:
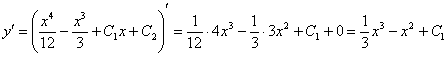
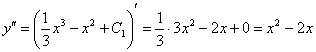
Получено исходное дифференциальное уравнение ![]() , значит, общее решение найдено правильно.
, значит, общее решение найдено правильно.
Пример 2
Решить дифференциальное уравнение
![]()
Это пример для самостоятельного решения. Как я уже где-то упоминал, иногда диффур может быть подшифрован. В предложенном примере сначала необходимо привести уравнение к стандартному виду ![]() . Решение и ответ в конце урока.
. Решение и ответ в конце урока.
Нахождение частного решения (задача Коши) имеет свои особенности, которые мы рассмотрим в следующих двух примерах:
Пример 3
Найти частное решение уравнения, соответствующее заданным начальным условиям
![]()
![]() ,
, ![]() ,
, ![]()
Решение: данное уравнение имеет вид ![]() . Согласно алгоритму, необходимо последовательно три раза проинтегрировать правую часть.
. Согласно алгоритму, необходимо последовательно три раза проинтегрировать правую часть.
Сначала понижаем степень уравнения до второго порядка:
![]()
Первый интеграл принёс нам константу ![]() . В уравнениях рассматриваемого типа рационально сразу же применять подходящие начальные условия.
. В уравнениях рассматриваемого типа рационально сразу же применять подходящие начальные условия.
Итак, у нас найдено ![]() , и, очевидно, к полученному уравнению подходит начальное условие
, и, очевидно, к полученному уравнению подходит начальное условие ![]() .
.
В соответствии с начальным условием ![]() :
:
![]()
Таким образом: ![]()
На следующем шаге берём второй интеграл, понижая степень уравнения до первого порядка:
![]()
Выползла константа ![]() , с которой мы немедленно расправляемся. Хах. Комментирую пример, а в голове возникла ассоциация, что я злой дед Мазай с одноствольным ружьём. Ну и действительно, константы отстреливаются, как только покажут уши из-под интеграла.
, с которой мы немедленно расправляемся. Хах. Комментирую пример, а в голове возникла ассоциация, что я злой дед Мазай с одноствольным ружьём. Ну и действительно, константы отстреливаются, как только покажут уши из-под интеграла.
В соответствии с начальным условием ![]() :
:
![]()
Таким образом: ![]()
И, наконец, третий интеграл:
![]()
Для третьей константы используем последний патрон ![]() :
:
![]()
Зайцы плачут, заряды были с солью.
Ответ: частное решение: ![]()
Выполним проверку, благо, она ненапряжная:
Проверяем начальное условие ![]() :
:
![]() – выполнено.
– выполнено.
Находим производную:
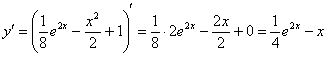
Проверяем начальное условие ![]() :
:
![]() – выполнено.
– выполнено.
Находим вторую производную:
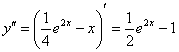
Проверяем начальное условие ![]() :
:
![]() – выполнено.
– выполнено.
Найдем третью производную:
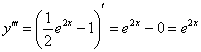
Получено исходное дифференциальное уравнение ![]()
Вывод: задание выполнено верно
Наверное, все обратили внимание на следующую вещь: каков порядок уравнения – столько и констант. Уравнение второго порядка располагает двумя константами ![]() , в уравнении третьего порядка – ровно три константы
, в уравнении третьего порядка – ровно три константы ![]() , в уравнении четвертого порядка обязательно будет ровно четыре константы
, в уравнении четвертого порядка обязательно будет ровно четыре константы ![]() и т. д. Причем, эта особенность справедлива вообще для любого диффура высшего порядка.
и т. д. Причем, эта особенность справедлива вообще для любого диффура высшего порядка.
Пример 4
Найти частное решение уравнения, соответствующее заданным начальным условиям
![]()
![]() ,
, ![]() ,
, ![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Время от времени в дифференциальных уравнениях рассматриваемого типа приходится находить более трудные интегралы: использовать метод замены переменной, интегрировать по частям, прибегать к другим ухищрениям. Я намеренно подобрал простые примеры без всяких замысловатостей, чтобы больше внимания уделить именно алгоритму решения.
В дифференциальном уравнении в явном виде отсутствует функция 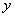
Диффур 2-го порядка этого типа в общем виде выглядит так:
![]() – всё есть, а «игрека» нет. Точнее, его нет в явном виде, но он обязательно всплывёт в ходе решения.
– всё есть, а «игрека» нет. Точнее, его нет в явном виде, но он обязательно всплывёт в ходе решения.
Кроме того, вместе с «игреком» в явном виде может отсутствовать первая производная:
![]() – это уже уравнение третьего порядка.
– это уже уравнение третьего порядка.
Может дополнительно отсутствовать и вторая производная:
![]() – уравнение четвертого порядка.
– уравнение четвертого порядка.
И так далее. Думаю, все увидели закономерность, и теперь смогут без труда определить такое уравнение в практических примерах. Кроме того, во всех этих уравнениях обязательно присутствует независимая переменная «икс».
На самом деле есть общая формула, строгая формулировка, но я стараюсь избегать лишних параметров и прочих математических наворотов, поскольку уроки носят не теоретический, а практический характер. И даже формулы, которые я только что привел, являются не совсем полными с теоретической точки зрения.
Как решать такие уравнения? Они решаются с помощью очень простой замены.
Пример 5
Найти общее решение дифференциального уравнения
![]()
Решение: в данном уравнении второго порядка в явном виде не участвует переменная ![]() . Заменим первую производную
. Заменим первую производную ![]() новой функцией
новой функцией ![]() , которая зависит от «икс»:
, которая зависит от «икс»:
![]()
Если ![]() , то
, то ![]()
Цель проведённой замены очевидна – понизить степень уравнения:
![]()
Получено линейное неоднородное уравнение первого порядка, с той лишь разницей, что вместо привычной функции «игрек» у нас функция «зет». Грубо говоря, отличие только в букве.
Линейное неоднородное уравнение первого порядка можно решить двумя способами: методом Бернулли (замены переменной) или методом вариации произвольной постоянной. Я выберу метод вариации произвольной постоянной, поскольку он маловато встречался в моих статьях.
Решим вспомогательное уравнение:
![]()
Разделяем переменные и интегрируем:
![]()
![]()
![]()
![]()
Общее решение вспомогательного уравнения: ![]()
Варьируя постоянную ![]() , в неоднородном уравнении
, в неоднородном уравнении ![]() проведем замену:
проведем замену:
![]()
![]()
Пара слагаемых в левой части взаимоуничтожается, значит, мы на верном пути:
![]()
Разделяем переменные и интегрируем:
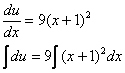
![]()
Таким образом:
![]()
Итак, функция ![]() найдена. Тут на радостях можно забыть про одну вещь и машинально записать ответ. Нет-нет, ещё не всё. Вспоминаем, что в начале задания была выполнена замена
найдена. Тут на радостях можно забыть про одну вещь и машинально записать ответ. Нет-нет, ещё не всё. Вспоминаем, что в начале задания была выполнена замена ![]() , следовательно, нужно провести обратную замену
, следовательно, нужно провести обратную замену ![]() :
:
![]()
Общее решение восстанавливаем интегрированием:
![]()
На заключительном этапе нарисовался партизан «игрек», который, как мы помним, в дифференциальное уравнение в явном виде не входил.
Ответ: общее решение: ![]()
В большинстве случае проверить и такие уравнения не составляет особого труда. Берём полученный ответ, находим первую и вторую производные:
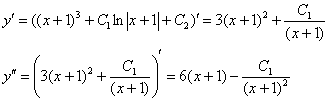
Подставим первую и вторую производную в исходное уравнение ![]() :
:
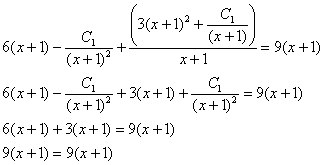
Получено верное равенство, значит, общее решение найдено правильно.
Пример 6
Решить дифференциальное уравнение
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Теперь вспомним начало заданий. С помощью замены ![]() мы понижали степень уравнения и получали линейное неоднородное уравнение первого порядка. Всегда ли получается именно линейное уравнение в результате замены? Так происходит часто, но не всегда. После замены
мы понижали степень уравнения и получали линейное неоднородное уравнение первого порядка. Всегда ли получается именно линейное уравнение в результате замены? Так происходит часто, но не всегда. После замены ![]() может получиться уравнение с разделяющимися переменными, однородное уравнение первого порядка, а также некоторые другие интересности.
может получиться уравнение с разделяющимися переменными, однородное уравнение первого порядка, а также некоторые другие интересности.
Пример 7
Решить дифференциальное уравнение
![]()
Решение: в данном уравнении третьего порядка в явном виде не участвуют функция ![]() и первая производная
и первая производная ![]() . Замена будет очень похожей, за «зет» обозначаем младшего брата:
. Замена будет очень похожей, за «зет» обозначаем младшего брата:
![]()
Если ![]() , то
, то ![]()
Таким образом, уравнение понижено до первого порядка:
![]()
Получено уравнение с разделяющимися переменными, разделяем переменные и интегрируем:
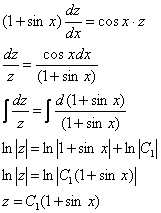
Проведем обратную замену: ![]()
![]()
Данное уравнение имеет уже знакомый с первого параграфа вид: ![]() .
.
Дважды интегрируем правую часть:
![]()
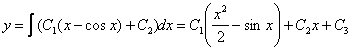
Ответ: общее решение: 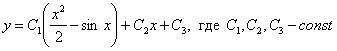
Пример 8
Найти общее решение дифференциального уравнения
![]()
Это пример для самостоятельного решения. После понижения степени получится линейное неоднородное уравнение первого порядка, которое в моём образце решено методом Бернулли. Как говорится, весь арсенал в ходу.
В дифференциальном уравнении
в явном виде отсутствует независимая переменная 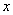
Третий, чуть более сложный тип уравнения, допускающий понижение порядка. Я не буду рисовать общих формул – отличительная особенность данного диффура состоит в том, что в нём в явном виде отсутствует независимая переменная «икс». То есть в исходном дифференциальном уравнении нет «икса». Вообще нет. Ни одного. Нигде.
Пример 9
Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям
![]() ,
, ![]() ,
, ![]()
Решение: в данном уравнении в явном виде не участвует переменная ![]() . Подстановка здесь более замысловата. Первую производную
. Подстановка здесь более замысловата. Первую производную ![]() заменим некоторой пока еще неизвестной функцией
заменим некоторой пока еще неизвестной функцией ![]() , которая зависит от функции «игрек»:
, которая зависит от функции «игрек»: ![]() . Обратите внимание, что функция
. Обратите внимание, что функция ![]() – это сложная функция. Внешняя функция – «зет», внутренняя функция – «игрек» («игрек» сам по себе является функцией).
– это сложная функция. Внешняя функция – «зет», внутренняя функция – «игрек» («игрек» сам по себе является функцией).
Находим вторую производную. По правилу дифференцирования сложной функции:
![]()
Учитывая, что ![]() , окончательно получаем:
, окончательно получаем: ![]()
В принципе, можно запомнить данную замену формально и коротко:
![]()
![]()
Другой вопрос, что студентам часто не понятно, почему в замене такая странная вторая производная: ![]() , «совершенно же очевидно, что должно быть
, «совершенно же очевидно, что должно быть ![]() ». А вот, оно, и не очевидно. Почему
». А вот, оно, и не очевидно. Почему ![]() , я только что подробно прокомментировал.
, я только что подробно прокомментировал.
Итак, в исходном уравнении ![]() проведём нашу замену:
проведём нашу замену:
![]()
Цель замены – опять же понизить порядок уравнения:
![]()
Одно «зет» сразу сокращаем:
![]()
Получено уравнение с разделяющимися переменными. Если ![]() – функция, зависящая от «игрек», то первая производная в дифференциалах расписывается так:
– функция, зависящая от «игрек», то первая производная в дифференциалах расписывается так:
![]() . Не допускаем машинальной ошибки – не пишем «привычное»
. Не допускаем машинальной ошибки – не пишем «привычное» ![]() !!!
!!!
Разделяем переменные и интегрируем:
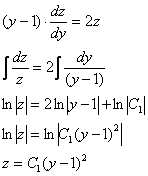
Проведем обратную замену ![]() :
:
![]()
Как и в первом параграфе, константу целесообразно отстрелить незамедлительно, это значительно упростит дальнейшее интегрирование.
Используем оба начальных условия одновременно: ![]() ,
, ![]()
В полученное уравнение ![]() подставим
подставим ![]() и
и ![]() :
:
![]()
Таким образом:
![]()
Дальнейшее просто:

Вторую константу тоже отстреливаем. Используя начальное условие ![]() , проводим подстановку
, проводим подстановку ![]() :
:
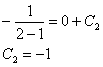
Таким образом: ![]()
Выразим частное решение в явном виде:
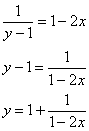
Ответ: частное решение: ![]()
Кстати, ответ легко проверяется.
Для закрепления материала пара заключительных примеров.
Пример 10
Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям
![]() ,
, ![]() ,
, ![]()
Решение: в данном уравнении в явном виде не участвует переменная ![]() . Еще здесь нет первой производной, но это не должно смущать – важно, что нет «иксов», а значит, используется стандартная замена:
. Еще здесь нет первой производной, но это не должно смущать – важно, что нет «иксов», а значит, используется стандартная замена:
![]()
Таким образом, степень уравнения понижена до первого порядка:
![]()
Разделяем переменные и интегрируем, не забывая, что ![]() :
:

Переобозначим константу ![]() через
через ![]() :
:
![]() .
.
Проведём обратную замену ![]() :
:
![]()
Используем одновременно оба начальных условия ![]() ,
, ![]() и найдём значение константы
и найдём значение константы ![]() . Для этого в полученное уравнение
. Для этого в полученное уравнение ![]() подставим
подставим ![]() и
и![]() :
:
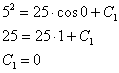
Таким образом:
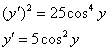
Разделяем переменные и интегрируем:
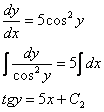
В соответствии с начальным условием ![]() :
:
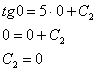
Окончательно: ![]() или
или ![]()
Ответ: частное решение: ![]()
Пример 11
Найти решение задачи Коши.
![]() ,
, ![]() ,
, ![]()
Это пример для самостоятельного решения.
Обратите внимание, что все три примера последнего параграфа идут с задачей Коши. Это не случайно. Специфика рассмотренного типа дифференциальных уравнений такова, что если предложить найти общее решение, то в большинстве уравнений нарисуются сложные, вычурные, а то и вообще неберущиеся интегралы. Поэтому практически всегда вам будет предложено найти частное решение.
Существуют еще некоторые типы диффуров, допускающие понижение порядка, но на практике они мне ни разу не встречались, хотя я перерешал очень много дифференциальных уравнений. Поэтому в урок были включены только те примеры, которые вам могут встретиться реально.
А сейчас пора повесить ружье на гвоздь и идти пить чай.
Удачного понижения степеней дифференциальных уравнений!
Решения и ответы:
Пример 2. Решение: преобразуем уравнение: ![]()
Данное ДУ имеет вид ![]() . Дважды интегрируем правую часть:
. Дважды интегрируем правую часть:
![]()
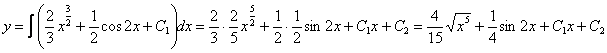
Ответ: общее решение: ![]()
Пример 4. Решение: преобразуем уравнение: ![]() .
.
Данное уравнение имеет вид ![]() . Трижды интегрируем правую часть:
. Трижды интегрируем правую часть:
![]()
В соответствии с начальным условием:
![]()
![]()
В соответствии с начальным условием:
![]()
![]()
В соответствии с начальным условием:
![]()
Ответ: частное решение: ![]()
Пример 6. Решение: в данное уравнение в явном виде не входит функция ![]() , проведем замену:
, проведем замену: ![]()
![]()
Получено линейное неоднородное уравнение первого порядка. Используем метод вариации произвольной постоянной. Решим вспомогательное уравнение:
![]()
Разделяем переменные и интегрируем:

В неоднородном уравнении проведем замену:
![]()
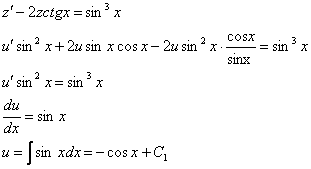
Таким образом:
![]()
Обратная замена: ![]()

Ответ: Общее решение: ![]()
Пример 8. Решение: Проведем замену: ![]()
![]()
Получено линейное неоднородное уравнение, замена: ![]()
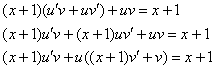
Составим и решим систему: ![]()
Из первого уравнения найдем ![]() :
:
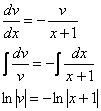
![]() – подставим во второе уравнение:
– подставим во второе уравнение:
![]()
![]()
![]()
Таким образом: 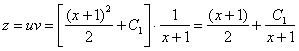
Обратная замена: ![]()
![]()
Дважды интегрируем правую часть:
![]()
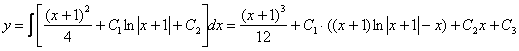
Здесь я немножко схалтурил, интеграл от логарифма берётся по частям, и, строго говоря, последний интеграл нужно расписать подробнее.
Ответ: общее решение:
![]()
Пример 11. Решение: в данном уравнении в явном виде не участвует переменная ![]() , проведем замену:
, проведем замену: ![]()

Обратная замена: ![]()
![]()
В соответствии с начальными условиями ![]() ,
, ![]() :
:
![]()
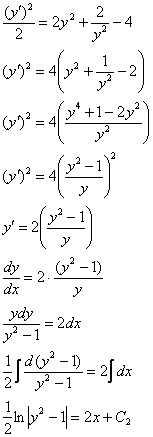
В соответствии с начальным условием ![]() :
:
![]()
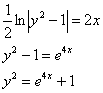
Ответ: частное решение: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright