Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Биномиальное распределение вероятностей

Или биномиальный закон распределения вероятностей. Исходя из моих наблюдений и личной статистики – это наиболее распространённый вид дискретного распределения, с которым мы уже встречались добрый десяток раз.

Я буду формулировать задачу в общем виде и попутно приводить конкретный пример:

Пусть проводится  независимых испытаний (не обязательно повторных), в каждом из которых случайное событие  может появиться с вероятностью. Тогда случайная величина  – число появлений события  в данной серии испытаний, имеет биномиальное распределение.

Совершенно понятно, что эта случайная величина может принять одно из следующих значений: .

Например: монета подбрасывается 5 раз. Тогда случайная величина  – количество появлений орла распределена по биномиальному закону. Орёл обязательно выпадет:

или  раз, или , или , или , или , или  раз.

Как вы догадались, соответствующие вероятности определяются формулой Бернулли:

, где:

 – количество независимых испытаний;
 – вероятность появления события  в каждом испытании;
 – вероятность непоявления события  в каждом испытании;
 – сколько раз может появиться событие  в данной серии испытаний (список всех возможных значений).

Сведём этот закон распределения в таблицу:

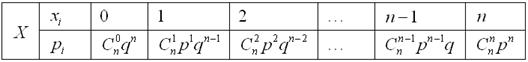
Вероятности  представляют собой члены бинома Ньютона, благодаря чему распределение и получило своё название. По формуле бинома:
, что мы и ожидали увидеть.

В нашем примере с монеткой:

 – вероятность того, что в 5 испытаниях орёл не выпадет вообще ();

 – вероятность того, что в 5 испытаниях орёл выпадет ровно  раз;

 – вероятность того, что в 5 испытаниях орёл выпадет ровно  раза;

 – … ровно  раза;

 – … ровно  раза;

 – … ровно  раз.

Таким образом, закон распределения числа выпавших орлов:

Контроль:

Легко видеть, что нахождение биномиального ряда распределения – есть занятие муторное, и это хорошо, если он содержит 3-4-5-6 значений. А ведь немало задач, где требуется рассчитать 8-10, а то и бОльшее количество вероятностей!

Поэтому вычисления целесообразно автоматизировать в Экселе с помощью его стандартной функции:

=БИНОМРАСП(m; n; p; 0), где  количество успехов в  испытаниях, а  – вероятность успеха в каждом испытании.

Именно так реализован Пункт 3 моего расчётного макета по ТерВеру, ну и особо крутая плюшка – это Пункт 6, в котором биномиальное распределение получается автоматически!

Однако на практике решение нужно расписывать подробно, да и техника не всегда бывает под рукой. В этой связи обязательно прорешайте хотя бы 2-3 типовых задачи и постукайте пальцами по клавишам микрокалькулятора.

Начинаем:

Задача

Вероятность поражения цели при одном выстреле равна 0,6. Составить закон распределения случайной величины  – числа попаданий в цель при четырех выстрелах. Вычислить  и . Построить многоугольник и функцию распределения. Найти .

…таких задач очень много – составить закон распределения вероятностей и найти всё-всё-всё. Или почти всё. Или что-то ещё – зависит от фантазии составителя :)

Решение: по существу, текст условия совпадает с Задачей статьи о геометрическом распределении, но есть одно принципиальное отличие – здесь другая случайная величина. А именно, под страхом расстрела совершается серия из  и строго из 4 выстрелов, вероятность попадания в каждом из которых составляет .

Очевидно, что испытания независимы, и случайная величина  распределена по биномиальному закону.

Составим ряд распределения данной случайной величины. Используем формулу Бернулли:
 для  – всех возможных результатов рассматриваемой серии.

На этом шаге я сразу забью  в свой расчётный макет (Пункт 6), чтобы контролировать правильность каждого пункта. Для удобства их можно нумеровать:

0)  
 – вероятность того, что в 4 выстрелах не будет попаданий;

1)
 – вероятность того, что в 4 выстрелах будет ровно 1 попадание;

2)
 – … ровно 2 попадания;

3)
 – … ровно 3 попадания;

4)
 – … ровно 4 попадания.

Таким образом, искомый закон распределения:

Проверка: , ч.т.п.

Пока таблица не ушла из поля зрения, построим многоугольник распределения:

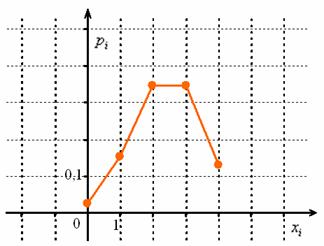
Вычислим математическое ожидание и дисперсию. И тут есть отличная новость – для биномиального распределения можно не использовать общий алгоритм расчёта этих числовых характеристик – по той причине, что существуют готовые формулы:

 – среднеожидаемое количество попаданий;

 – рассеяние количества попаданий относительно матожидания.

Всегда бы так!

Составим функцию распределения вероятностей:

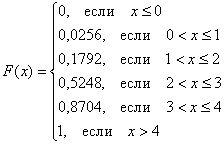
Я не буду вновь останавливаться на алгоритме её построения, и если что-то не понятно, то смотрите по ссылке выше. Раз ступенька, два ступенька – будет график:

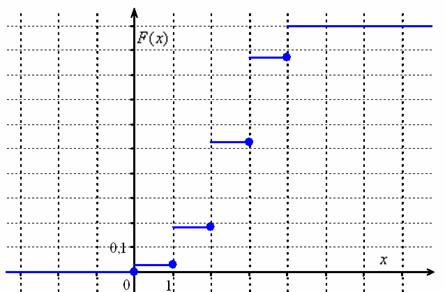
Напоминаю, что в статье о функции распределения можно разыскать программу, которая строит чертежи автоматически.

Найдём  – вероятность того, что значение случайной величины  отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение.

Среднее квадратическое отклонение:

и искомая вероятность:

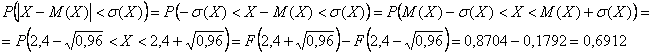
(в чём смысл этого пункта решения?)

Готово.

Как вариант, в разобранной задаче может быть предложена другая случайная величина: не количество попаданий, а  – количество промахов. Нетрудно догадаться, что в этом случае вероятности «развернутся наоборот» , и числовые характеристики с графиками будут другими.

БУДЬТЕ ВНИМАТЕЛЬНЫ!

Дополнительные и многочисленные задания по теме можно найти в pdf-сборнике, и как я рекомендовал выше – непременно прорешайте пару-тройку задач вручную! Как говорится, автопилот хорошо, но без ручного управления – финиш.

На очереди распределение Пуассона и гипергеометрическое распределение вероятностей.

Желаю успехов!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте