


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Простейшие задачи с прямой на плоскости.
Взаимное расположение прямых. Угол между прямыми
Продолжаем рассматривать эти бесконечные-бесконечные прямые. На уроке Уравнение прямой на плоскости мы познакомились с основными видами уравнений, направляющим вектором прямой и её вектором нормали. Данная статья является логическим продолжением темы, и в ней будут разобраны следующие типовые задачи, для опытных путешественников телепортация:
- Как определить взаимное расположение двух прямых?
- Как построить прямую, параллельную данной?
- Как найти точку пересечения двух прямых?
- Как построить прямую, перпендикулярную данной?
- Как найти расстояние от точки до прямой?
- Как построить точку, симметричную относительно прямой?
- Как найти расстояние между двумя параллельными прямыми?
- Как найти угол между двумя прямыми? Три способа
О-о-о-о-о… Ну и жесть, словно вам сам себе приговор зачитал =) Впрочем, потом релаксация поможет, тем более, сегодня купил подходящие аксессуары. Поэтому приступим к первому разделу, надеюсь, к концу статьи сохраню бодрое расположение духа.
Взаимное расположение двух прямых
Рассмотрим две прямые, заданные уравнениями в общем виде:
![]()
Тот случай, когда зал подпевает хором. Две прямые могут:
1) совпадать;
2) быть параллельными: ![]() ;
;
3) или пересекаться в единственной точке: ![]() .
.
Справка для чайников: пожалуйста, запомните математический знак пересечения ![]() , он будет встречаться очень часто. Запись
, он будет встречаться очень часто. Запись ![]() обозначает, что прямая
обозначает, что прямая ![]() пересекается с прямой
пересекается с прямой ![]() в точке
в точке ![]() .
.
Как определить взаимное расположение двух прямых?
Начнём с первого случая:
две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть существует такое число «лямбда», что выполняются равенства ![]()
Рассмотрим прямые ![]() и составим три уравнения из соответствующих коэффициентов:
и составим три уравнения из соответствующих коэффициентов: ![]() . Из каждого уравнения следует, что
. Из каждого уравнения следует, что ![]() , следовательно, данные прямые совпадают.
, следовательно, данные прямые совпадают.
Действительно, если все коэффициенты уравнения ![]() умножить на –1 (сменить знаки), и все коэффициенты уравнения
умножить на –1 (сменить знаки), и все коэффициенты уравнения ![]() сократить на 2, то получится одно и то же уравнение:
сократить на 2, то получится одно и то же уравнение: ![]() .
.
Второй случай, когда прямые параллельны:
две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных ![]() пропорциональны:
пропорциональны: ![]() , но
, но ![]() .
.
В качестве примера рассмотрим две прямые ![]() . Проверяем пропорциональность соответствующих коэффициентов при переменных
. Проверяем пропорциональность соответствующих коэффициентов при переменных ![]() :
:
![]()
Однако совершенно очевидно, что ![]() .
.
Вывод: ![]()
И третий случай, когда прямые пересекаются:
две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных ![]() НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства
НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства ![]()
Так, для прямых ![]() составим систему:
составим систему:
![]()
Из первого уравнения следует, что ![]() , а из второго уравнения:
, а из второго уравнения: ![]() , значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных
, значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных ![]() не пропорциональны.
не пропорциональны.
Вывод: прямые пересекаются
В практических задачах можно использовать только что рассмотренную схему решения. Она, кстати, весьма напоминает алгоритм проверки векторов на коллинеарность, который мы рассматривали на уроке Понятие линейной (не) зависимости векторов. Базис векторов. Но существует более цивилизованная упаковка:
Пример 1
Выяснить взаимное расположение прямых:
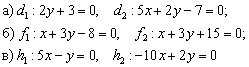
Решение основано на исследовании направляющих векторов прямых:
а) Из уравнений ![]() найдём направляющие векторы прямых:
найдём направляющие векторы прямых: ![]() .
.
Вычислим определитель, составленный из координат данных векторов:
![]() , значит, векторы
, значит, векторы ![]() не коллинеарны и прямые
не коллинеарны и прямые ![]() пересекаются.
пересекаются.
На всякий случай поставлю на распутье камень с указателями:
1) Если мало что понятно, начните со статьи Векторы для чайников.
2) Если не понятно, как находить направляющие векторы, посетите урок Уравнение прямой на плоскости.
3) Если неясно, причём тут определитель, вам сюда – Понятие линейной (не) зависимости векторов. Базис векторов.
Остальные перепрыгивают камень и следуют дальше, прямо к Кащею Бессмертному =)
б) Найдем направляющие векторы прямых ![]() :
:
![]()
Прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают. Тут и определитель считать не надо.
Очевидно, что коэффициенты при переменных ![]() пропорциональны, при этом
пропорциональны, при этом ![]() .
.
Выясним, справедливо ли равенство ![]() :
:
![]()
Таким образом, ![]()
в) Найдем направляющие векторы прямых ![]() :
:
![]()
Вычислим определитель, составленный из координат данных векторов:
![]() , следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.
, следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.
Коэффициент пропорциональности «лямбда» нетрудно усмотреть прямо из соотношения коллинеарных направляющих векторов ![]() . Впрочем, его можно найти и через коэффициенты самих уравнений:
. Впрочем, его можно найти и через коэффициенты самих уравнений: ![]() .
.
Теперь выясним, справедливо ли равенство ![]() . Оба свободных члена нулевые, поэтому:
. Оба свободных члена нулевые, поэтому:
![]()
Полученное значение ![]() удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).
удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).
Таким образом, прямые совпадают.
Ответ: ![]()
Очень скоро вы научитесь (или даже уже научились) решать рассмотренную задачу устно буквально в считанные секунды. В этой связи не вижу смысла предлагать что-либо для самостоятельного решения, лучше заложим ещё один важный кирпич в геометрический фундамент:
как построить прямую, параллельную данной?
За незнание этой простейшей задачи сурово наказывает Соловей-Разбойник.
Пример 2
Прямая задана уравнением ![]() . Составить уравнение параллельной прямой, которая проходит через точку
. Составить уравнение параллельной прямой, которая проходит через точку ![]() .
.
Решение: обозначим неизвестную прямую буквой ![]() . Что о ней сказано в условии? Прямая
. Что о ней сказано в условии? Прямая ![]() проходит через точку
проходит через точку ![]() . А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для построения прямой «дэ».
. А если прямые параллельны, то очевидно, что направляющий вектор прямой «цэ» подойдёт и для построения прямой «дэ».
Вытаскиваем направляющий вектор из уравнения ![]() :
:
![]()
Уравнение прямой ![]() составим по точке
составим по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
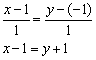
Ответ: ![]()
Геометрия примера выглядит незатейливо:
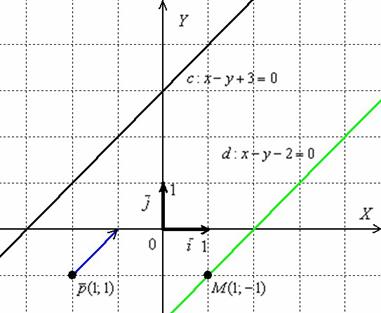
Аналитическая же проверка состоит в следующих шагах:
1) Проверяем, что у прямых ![]() один и тот же направляющий вектор (если уравнение прямой не упрощено должным образом, то векторы будут коллинеарны).
один и тот же направляющий вектор (если уравнение прямой не упрощено должным образом, то векторы будут коллинеарны).
2) Проверяем, удовлетворяет ли точка ![]() полученному уравнению
полученному уравнению ![]() .
.
Аналитическую проверку в большинстве случаев легко выполнить устно. Посмотрите на два уравнения, и многие из вас быстро определят параллельность прямых безо всякого чертежа.
Примеры для самостоятельного решения сегодня будут творческими. Потому что вам ещё придётся тягаться с Бабой-Ягой, а она, знаете, любительница всяких загадок.
Пример 3
Составить уравнение прямой, проходящей через точку ![]() , параллельную прямой
, параллельную прямой ![]() , если
, если ![]()
Существует рациональный и не очень рациональный способ решения. Самый короткий путь – в конце урока.
С параллельными прямыми немного поработали и к ним ещё вернёмся. Случай совпадающих прямых малоинтересен, поэтому рассмотрим задачу, которая хорошо знакома вам из школьной программы:
как найти точку пересечения двух прямых?
Если прямые ![]() пересекаются в точке
пересекаются в точке ![]() , то её координаты являются решением системы линейных уравнений
, то её координаты являются решением системы линейных уравнений ![]()
Как найти точку пересечения прямых? Решить систему.
Вот вам и геометрический смысл системы двух линейных уравнений с двумя неизвестными – это две пересекающиеся (чаще всего) прямые на плоскости.
Пример 4
Найти точку пересечения прямых ![]()
Существуют два способа решения – графический и аналитический.
Графический способ состоит в том, чтобы просто начертить данные прямые и узнать точку пересечения непосредственно из чертежа:
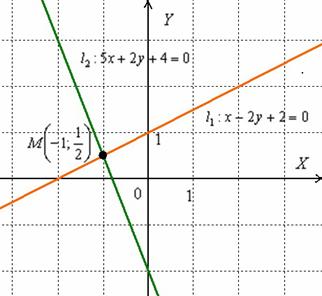
Вот наша точка: ![]() . Для проверки следует подставить её координаты в каждое уравнение, они должны подойти и там, и там. Иными словами, координаты точки
. Для проверки следует подставить её координаты в каждое уравнение, они должны подойти и там, и там. Иными словами, координаты точки ![]() являются решением системы
являются решением системы ![]() . По сути, мы рассмотрели графический способ решения системы линейных уравнений с двумя уравнениями, двумя неизвестными.
. По сути, мы рассмотрели графический способ решения системы линейных уравнений с двумя уравнениями, двумя неизвестными.
Графический способ, конечно, неплох, но существует заметные минусы. Нет, дело не в том, что так решают семиклассники, дело в том, что на правильный и ТОЧНЫЙ чертёж уйдёт время. Кроме того, некоторые прямые построить не так-то просто, да и сама точка пересечения может находиться где-нибудь в тридесятом царстве за пределами тетрадного листа.
Поэтому точку пересечения ![]() целесообразнее искать аналитическим методом. Решим систему:
целесообразнее искать аналитическим методом. Решим систему:
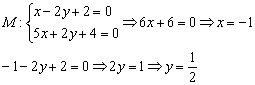
Для решения системы использован метод почленного сложения уравнений.
Ответ: ![]()
Проверка тривиальна – координаты точки пересечения должны удовлетворять каждому уравнению системы.
Пример 5
Найти точку пересечения прямых ![]() в том случае, если они пересекаются.
в том случае, если они пересекаются. ![]()
Это пример для самостоятельного решения. Задачу удобно разбить на несколько этапов. Анализ условия подсказывает, что нужно:
1) Составить уравнение прямой ![]() .
.
2) Составить уравнение прямой ![]() .
.
3) Выяснить взаимное расположение прямых ![]() .
.
4) Если прямые пересекаются, то найти точку пересечения.
Разработка алгоритма действий типична для многих геометрических задач, и я на этом буду неоднократно заострять внимание.
Полное решение и ответ в конце урока:
Ещё не стоптана и пара башмаков, как мы подобрались ко второму разделу урока:
Перпендикулярные прямые. Расстояние от точки до прямой.
Угол между прямыми
Начнём с типовой и очень важной задачи. В первой части мы узнали, как построить прямую, параллельную данной, а сейчас избушка на курьих ножках развернётся на 90 градусов:
как построить прямую, перпендикулярную данной?
Пример 6
Прямая задана уравнением ![]() в декартовой системе координат. Составить уравнение перпендикулярной прямой
в декартовой системе координат. Составить уравнение перпендикулярной прямой ![]() , проходящей через точку
, проходящей через точку ![]() .
.
Решение: по условию известно, что ![]() . Неплохо бы найти направляющий вектор прямой
. Неплохо бы найти направляющий вектор прямой ![]() . Поскольку прямые перпендикулярны, фокус прост:
. Поскольку прямые перпендикулярны, фокус прост:
Из уравнения ![]() «снимаем» вектор нормали:
«снимаем» вектор нормали: ![]() , который и будет направляющим вектором прямой
, который и будет направляющим вектором прямой ![]() .
.
Уравнение прямой ![]() составим по точке
составим по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
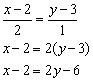
Ответ: ![]()
Развернём геометрический этюд:
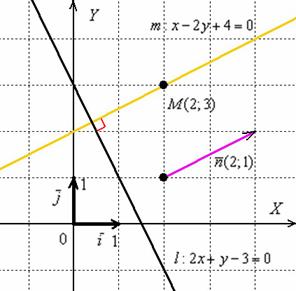
М-да… Оранжевое небо, оранжевое море, оранжевый верблюд.
Аналитическая проверка решения:
1) Из уравнений ![]() вытаскиваем направляющие векторы
вытаскиваем направляющие векторы ![]() и с помощью скалярного произведения векторов приходим к выводу, что прямые действительно перпендикулярны:
и с помощью скалярного произведения векторов приходим к выводу, что прямые действительно перпендикулярны: ![]() .
.
Кстати, можно использовать векторы нормали, это даже проще.
2) Проверяем, удовлетворяет ли точка ![]() полученному уравнению
полученному уравнению ![]() .
.
Проверку, опять же, легко выполнить устно.
Пример 7
Найти точку пересечения перпендикулярных прямых ![]() , если известно уравнение
, если известно уравнение ![]() в декартовой системе координат и точка
в декартовой системе координат и точка ![]() .
.
Это пример для самостоятельного решения. В задаче несколько действий, поэтому решение удобно оформить по пунктам.
Наше увлекательное путешествие продолжается.
Расстояние от точки до прямой
Перед нами прямая полоса реки и наша задача состоит в том, чтобы дойти до неё кратчайшим путём. Препятствий нет, и самым оптимальным маршрутом будет движение по перпендикуляру. То есть расстояние от точки до прямой – это длина перпендикулярного отрезка.
Расстояние в геометрии традиционно обозначают греческой буквой «ро», например: ![]() – расстояние от точки «эм» до прямой «дэ».
– расстояние от точки «эм» до прямой «дэ».
Расстояние от точки ![]() до прямой
до прямой ![]() , заданной в декартовой системе координат, выражается формулой
, заданной в декартовой системе координат, выражается формулой
![]()
Пример 8
Найти расстояние от точки ![]() до прямой
до прямой ![]()
Решение: всё что нужно, это аккуратно подставить числа в формулу и провести вычисления:
![]()
Ответ: ![]()
Выполним чертёж:
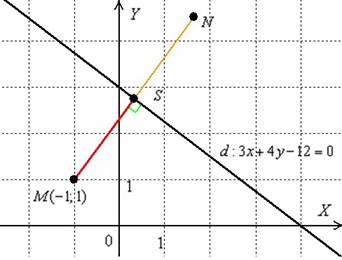
Найденное расстояние от точки до прямой – это в точности длина красного отрезка. Если оформить чертёж на клетчатой бумаге в масштабе 1 ед. = 1 см (2 клетки), то расстояние можно измерить обыкновенной линейкой.
Рассмотрим ещё одно задание по этому же чертежу:
как построить точку, симметричную относительно прямой?
Задача состоит в том, чтобы найти координаты точки ![]() , которая симметрична точке
, которая симметрична точке ![]() относительно прямой
относительно прямой ![]() . Предлагаю выполнить действия самостоятельно, однако обозначу алгоритм решения с промежуточными результатами:
. Предлагаю выполнить действия самостоятельно, однако обозначу алгоритм решения с промежуточными результатами:
1) Находим прямую ![]() , которая перпендикулярна прямой
, которая перпендикулярна прямой ![]() .
.
2) Находим точку пересечения прямых: ![]() .
.
Оба действия подробно разобраны в рамках данного урока.
3) Точка ![]() является серединой отрезка
является серединой отрезка ![]() . Нам известны координаты середины и одного из концов. По формулам координат середины отрезка находим
. Нам известны координаты середины и одного из концов. По формулам координат середины отрезка находим ![]() .
.
Не лишним будет проверить, что расстояние ![]() тоже равно 2,2 единицам.
тоже равно 2,2 единицам.
Трудности здесь могут возникнуть в вычислениях, но в вышке здорово выручает калькулятор, позволяющий считать обыкновенные дроби. И у нас есть свой фирменный «дробовик», если вы до сих пор его не заметили. Неоднократно советовал, посоветую и снова.
Как найти расстояние между двумя параллельными прямыми?
Пример 9
Найти расстояние ![]() между двумя параллельными прямыми
между двумя параллельными прямыми ![]()
![]() , заданными в декартовой системе координат.
, заданными в декартовой системе координат.
Это очередной пример для самостоятельного решения. Немного подскажу: тут бесконечно много способов решения. Разбор полётов в конце урока, но лучше постарайтесь догадаться сами, думаю, вашу смекалку удалось неплохо разогнать.
Угол между двумя прямыми
Что ни угол, то косяк:
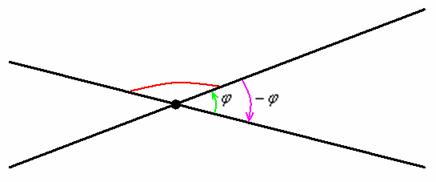
В геометрии за угол между двумя прямыми принимается МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом между пересекающимися прямыми. А считается таковым его «зелёный» сосед ![]() или противоположно ориентированный «малиновый» угол
или противоположно ориентированный «малиновый» угол ![]() .
.
Если прямые перпендикулярны, то за угол между ними можно принимать любой из 4 углов.
Чем отличаются углы ![]() ? Ориентацией. Во-первых, принципиально важным является направление «прокрутки» угла. Во-вторых, отрицательно ориентированный угол записывается со знаком «минус», например, если
? Ориентацией. Во-первых, принципиально важным является направление «прокрутки» угла. Во-вторых, отрицательно ориентированный угол записывается со знаком «минус», например, если ![]() .
.
Зачем я это рассказал? Вроде бы можно обойтись и обычным понятием угла. Дело в том, что в формулах, по которым мы будем находить углы, запросто может получиться отрицательный результат, и это не должно застать вас врасплох. Угол со знаком «минус» ничем не хуже, и имеет вполне конкретный геометрический смысл. На чертеже для отрицательного угла следует обязательно указывать стрелкой его ориентацию (по часовой стрелке).
Как найти угол между двумя прямыми? Существуют две рабочие формулы:
Пример 10
Найти угол между прямыми ![]()
Решение и способ первый
Рассмотрим две прямые, заданные общими уравнениями в декартовой системе координат:
![]()
Если прямые не перпендикулярны, то ориентированный угол ![]() между ними можно вычислить с помощью формулы:
между ними можно вычислить с помощью формулы:
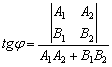
Самое пристальное внимание обратим на знаменатель – это в точности скалярное произведение направляющих векторов прямых:
![]()
Если ![]() , то знаменатель формулы обращается в ноль, а векторы будут ортогональны и прямые перпендикулярны. Именно поэтому сделана оговорка о неперпендикулярности прямых в формулировке.
, то знаменатель формулы обращается в ноль, а векторы будут ортогональны и прямые перпендикулярны. Именно поэтому сделана оговорка о неперпендикулярности прямых в формулировке.
Исходя из вышесказанного, решение удобно оформить в два шага:
1) Вычислим скалярное произведение направляющих векторов прямых:
![]() , значит, прямые не перпендикулярны.
, значит, прямые не перпендикулярны.
2) Угол между прямыми найдём по формуле:
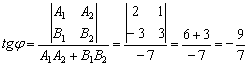
С помощью обратной функции легко найти и сам угол. При этом используем нечётность арктангенса (см. Графики и свойства элементарных функций):
![]()
Ответ: ![]()
В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью калькулятора.
Ну, минус, так минус, ничего страшного. Вот геометрическая иллюстрация:
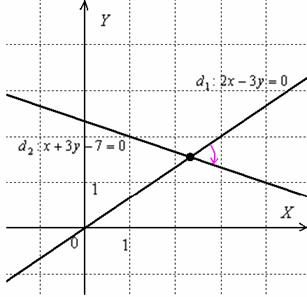
Неудивительно, что угол получился отрицательной ориентации, ведь в условии задачи первым номером идёт прямая ![]() и «открутка» угла началась именно с неё.
и «открутка» угла началась именно с неё.
Если очень хочется получить положительный угол, нужно поменять прямые местами, то есть коэффициенты ![]() взять из второго уравнения
взять из второго уравнения ![]() , а коэффициенты
, а коэффициенты ![]() взять из первого уравнения
взять из первого уравнения ![]() . Короче говоря, начать нужно с прямой
. Короче говоря, начать нужно с прямой ![]() .
.
Утаивать не буду, сам подбираю прямые в том порядке, чтобы угол получился положительным. Так красивее, но не более того.
Для проверки решения можно взять транспортир и измерить угол.
Способ второй
Если прямые заданы уравнениями с угловым коэффициентом ![]() (декартовы координаты) и не перпендикулярны, то ориентированный угол
(декартовы координаты) и не перпендикулярны, то ориентированный угол ![]() между ними можно найти с помощью формулы:
между ними можно найти с помощью формулы:
![]()
Условие перпендикулярности прямых выражается равенством ![]() , откуда, кстати, следует очень полезная взаимосвязь угловых коэффициентов перпендикулярных прямых:
, откуда, кстати, следует очень полезная взаимосвязь угловых коэффициентов перпендикулярных прямых: ![]() , которая используется, в частности при нахождении уравнения нормали.
, которая используется, в частности при нахождении уравнения нормали.
Алгоритм решения похож на предыдущий пункт. Но сначала перепишем наши прямые в нужном виде:
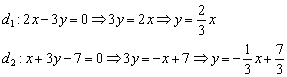
Таким образом, угловые коэффициенты: ![]()
1) Проверим, будут ли прямые перпендикулярны:
![]() , значит, прямые не перпендикулярны.
, значит, прямые не перпендикулярны.
2) Используем формулу:
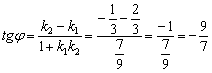
Ответ: ![]()
Второй способ уместно использовать тогда, когда уравнения прямых изначально заданы с угловым коэффициентом. Следует отметить, что если хотя бы одна прямая параллельна оси ординат, то формула не применима вообще, поскольку для таких прямых угловой коэффициент не определён (см. статью Уравнение прямой на плоскости).
Есть и третий способ решения. Идея состоит в том, чтобы вычислить угол между направляющими векторами прямых с помощью формулы, рассмотренной на уроке Скалярное произведение векторов:
![]()
Здесь уже речь идёт не об ориентированном угле, а «просто об угле», то есть результат заведомо будет положительным. Загвоздка состоит в том, что может получиться тупой угол (не тот, который нужен). В этом случае придётся делать оговорку, что угол между прямыми – это меньший угол, и из «пи» радиан (не из 180 градусов!) вычитать получившийся арккосинус.
Желающие могут прорешать задачу третьим способом. Но я рекомендую всё-таки придерживаться первого подхода с ориентированным углом, по той причине, что он широко распространён.
Пример 11
Найти угол между прямыми ![]() , заданными в декартовой системе координат.
, заданными в декартовой системе координат.
Это пример для самостоятельного решения. Попробуйте решить его двумя способами.
Как-то заглохла по ходу дела сказка…. Потому что нет никакого Кащея Бессмертного. Есть я, причём, не особо запаренный. Если честно, думал, статья значительно длиннее выйдет. Но все равно возьму недавно приобретенную шапочку с очками и пойду купаться в сентябрьской озёрной воде. Отлично снимает усталость и негативную энергетику.
До скорых встреч!
И помните, Бабу-Ягу никто не отменял =)
Решения и ответы:
Пример 3. Решение: найдём направляющий вектор прямой ![]() :
:
![]()
Уравнение искомой прямой составим по точке ![]() и направляющему вектору
и направляющему вектору ![]() . Так как одна из координат направляющего вектора нулевая, уравнение
. Так как одна из координат направляющего вектора нулевая, уравнение ![]() перепишем в виде:
перепишем в виде:
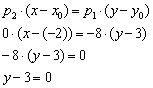
Ответ: ![]()
Пример 5. Решение:
1) Уравнение прямой ![]() составим по двум точкам
составим по двум точкам ![]() :
:
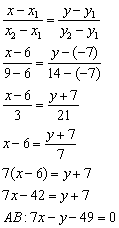
2) Уравнение прямой ![]() составим по двум точкам
составим по двум точкам ![]() :
:
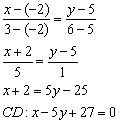
3) Соответствующие коэффициенты при переменных ![]() не пропорциональны:
не пропорциональны: ![]() , значит, прямые пересекаются.
, значит, прямые пересекаются.
4) Найдём точку ![]() :
:
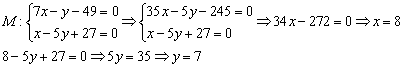
Примечание: здесь первое уравнение системы умножено на 5, затем из 1-го уравнения почленно вычтено 2-е.
Ответ: ![]()
Пример 7. Решение:
1) Найдём нормальный вектор прямой: ![]() .
.
2) Составим уравнение прямой ![]() по точке
по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
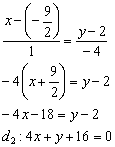
3) Найдём точку пересечения прямых ![]() :
:
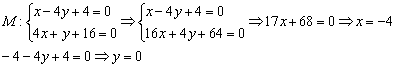
Примечание: второе уравнение умножено на 4, затем уравнения сложены почленно.
Ответ: ![]()
Пример 9. Решение: расстояние между параллельными прямыми найдём как расстояние от точки до прямой. Для этого достаточно найти одну точку, принадлежащую любой из прямых. В целях удобного подбора точки перепишем уравнение ![]() в виде уравнения с угловым коэффициентом:
в виде уравнения с угловым коэффициентом: ![]() . Точка
. Точка ![]() . Вычислим расстояние:
. Вычислим расстояние:
![]()
Последним действием числитель и знаменатель умножен на ![]() – чтобы избавиться от иррациональности в знаменателе.
– чтобы избавиться от иррациональности в знаменателе.
Ответ: ![]()
Пример 11. Решение, способ первый:
1) Вычислим скалярное произведение направляющих векторов прямых:
![]() , значит, прямые не перпендикулярны.
, значит, прямые не перпендикулярны.
2) Угол между прямыми найдём с помощью формулы:
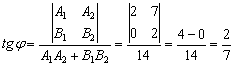
Таким образом:
![]()
Ответ: ![]()
Способ второй применить нельзя, так ак прямая ![]() параллельна оси ординат, и её угловой коэффициент не определён.
параллельна оси ординат, и её угловой коэффициент не определён.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright