Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Как вычислить предел функции с помощью ряда?

Этот коротенький урок посвящён ещё одному приложению степенных рядов, название которого вы видите в заголовке. Для решения примеров нам опять потребуется таблица разложений (откройте на соседней вкладке или распечатайте), и я предлагаю вам улучшить своё настроение! Потому что задание будет простое, приятное и его краткая суть такова: в некоторых пределах для устранения неопределённости оказывается эффективной замена функции(й) степенными рядами. Когда слова излишни:

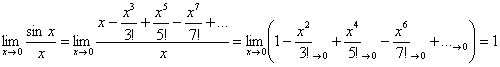
И сразу обратите внимание на одну важную особенность: многие приложения степенных рядов посвящены приближённым вычислениям, однако в данном случае мы имеем дело с точным методом – поскольку меняем функцию на ВЕСЬ ряд. Если вам всё же не понятна суть этого действия, то, пожалуйста, обратитесь к статье о разложении функций.

Аналогичным способом можно доказать некоторые другие замечательные пределы:

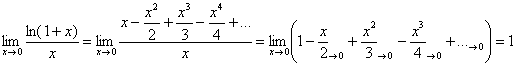
Задание: используя таблицу разложений, проверьте, что . Задание, в общем-то, устное.

Очевидно, что предельное значение «икс» должно обязательно лежать в интервале сходимости ряда, и теоретически это может быть любое число данного интервала. Но практически оно, как правило, равно нулю, что избавляет нас от проблем с «хвостом» ряда.

Пройдёмся по «местам боевой славы»:

Пример 1

Вычислить предел с помощью разложения функции в ряд

Это предел из Примера 4 статьи Замечательный пределы.

Используем разложение  – много членов записывать не нужно, обычно хватает трёх-четырёх. В данном случае :

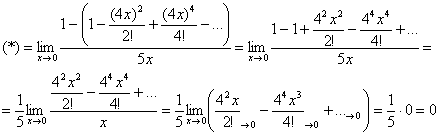
Не забываем проставлять троеточия и указывать, что остаток ряда стремится к нулю!

Тренируемся самостоятельно:

Пример 2

Вычислить предел с помощью степенных рядов

Краткое решение в конце урока. Сверьтесь с Примером 6 урока Правила Лопиталя.

И особо интересный предел (см. Пример 4 того же урока), в котором мы использовали правило Лопиталя дважды:

Пример 3

Вычислить предел с помощью степенных рядов

Вполне возможно, кому-то такое решение придётся больше по вкусу:

Используем разложение  для   и , и чтобы не запутаться, сразу упростим числитель:

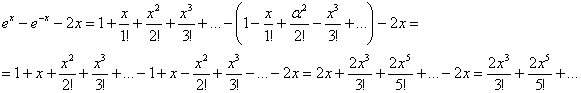
Со знаменателем всё проще:

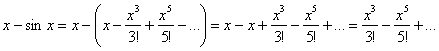
Таким образом:

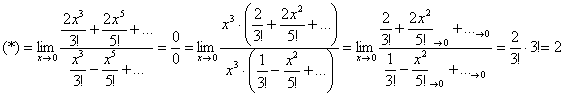
Рассматриваемый способ решения не является какой-то «проформой» и бывает действительно выгоден –  когда в «начинке» предела находятся «разношёрстные» функции, особенно их суммы или разности:

Пример 4

Пользуясь известными разложениями функций в ряд Маклорена, вычислить следующий предел:

Пользуйтесь =)

И даже в такой коротенькой статье не могу не порадовать вас новым и познавательным материалом!

Разложение тангенса в ряд Маклорена

 , где  – так называемые числа Бернулли. Данный ряд сходится при .

Вы спросите, почему разложения тангенса нет в таблице? Почти не требуется. ПризнАюсь, что данная «таблица» – это вообще не какая-то стандартная справка, а конспект, составленный на основе своего личного опыта. Так, например, во многих аналогичных «таблицах» вы не встретите разложения арктангенса и арксинуса (они выводятся – см. урок о сумме степенного ряда). Я же счёл нужным добавить их в pdf-ку, чтобы «далеко не ходить» – часто нужны на практике

Но вернёмся к теме:

Пример 5

Да, конечно, здесь можно воспользоваться тригонометрической формулой , избавиться от трёхэтажности дроби и разобраться с двумя синусами и  косинусом. Но к чему такие трудности? – если есть прямое разложение  для :

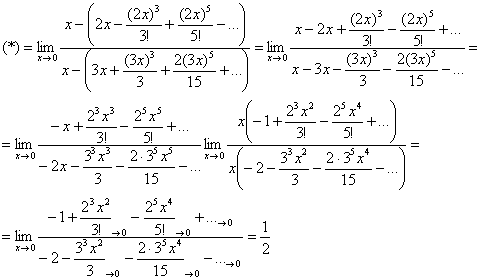
Ради шутки можете вычислить предел   из Примера 3 урока Замечательные пределы. А кроме шуток, разложение функций в ряд используется для устранения не только неопределённости  (как можно было бы подумать):

Пример 6

Вычислить предел с помощью степенного ряда

И при такой формулировке задания правила хорошего тона предписывают разложить экспоненту в ряд как можно скорее – ещё в знаменателе. Далее алгоритм работает стандартно: приводим выражение к общему знаменателю, после чего что-нибудь должно сократиться:

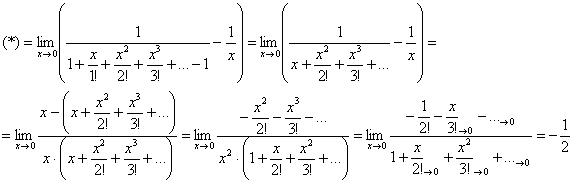
И заключительный предел для самостоятельного решения:

Пример 7

Вычислить предел, разложив функции в ряд Маклорена

Не знаете, что делать с квадратом синуса? Ай-яй-яй =)

Всё.

Решения и ответы:

Пример 2:
Используем ряд  и разложение  для :

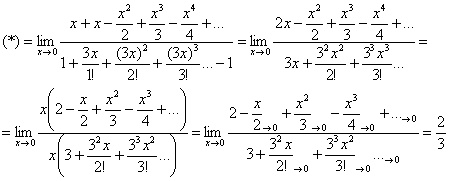
Пример 4:
Используем разложения  и :

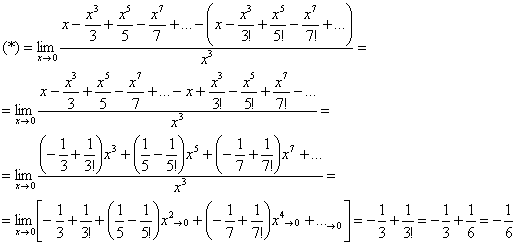
Пример 7:
Используем тригонометрическую формулу  и разложение  для :

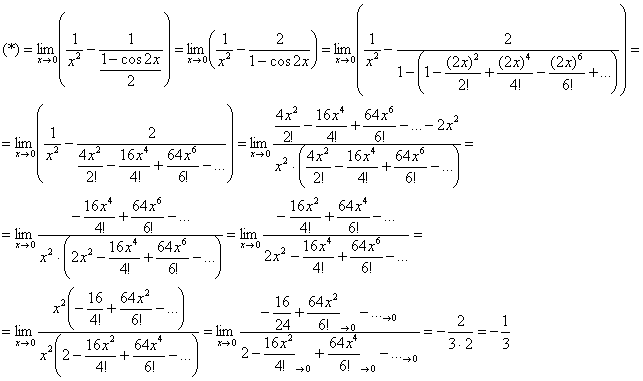
Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте