Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Система случайных величин. Задачи с решениями

Одна случайная величина – хорошо, а две – лучше, а ещё лучше – их система, которую также называют двумерной случайной величиной. Кроме того, можно рассмотреть системы трёх и бОльшего количества величин, но это уже будет слишком хорошо, а оно, как известно, плохо :)  Продолжаем разговор о случайных величинах (СВ), и для тех, кто не в теме, я сразу привёл ссылку выше. Для более подготовленных читателей тоже сразу:

– на ближайших уроках будут разобраны распространённые задачи с двумерной случайной величиной и кратко освещены соответствующие теоретические моменты.

План такой, нам с тобой:

• В этой статье рассмотрим самые-самые популярные вещи, которые предлагаются даже студентам-заочникам. Это простейшие примеры с двумерной дискретной, а также составной одномерной СВ наподобие 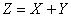. + Матожидания, дисперсии и иже с ними.
• Далее остановимся на задачах с дискретной зависимой случайной величиной, условных законах распределения и узнаем, как находить коэффициенты ковариации и корреляции.
• Двумерная непрерывная случайная величина, функция распределения и функция плотности распределения. С подробными объяснениями примерами и эксклюзивными чертежами
• И, наконец, условные законы распределения и коэффициент ковариации двумерной непрерывной СВ.

Ещё раз подчёркиваю, что будет, в основном, практика, и если вам нужны развернутые теоретические выкладки, то рекомендую обратиться к одному из последних изданий учебного пособия В.Е. Гмурмана, которое переиздаётся более 50 лет, и в представлении не нуждается.

Ну а меня зовут Александр Емелин (кто не знает), и я с энтузиазмом присматриваюсь к следующему столетию:)

Вспоминаем первый урок по теме и эталонный пример с игральным кубиком (костью), где мы рассмотрели случайную величину  – количество очков, выпавших в результате его броска. В правильных руках правильный кубик даёт следующий закон распределения вероятностей:

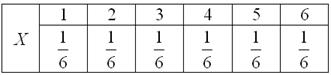
Теперь рассмотрим другой такой же кубик и случайную величину  – количество очков, выпавших на этом кубике. Очевидно, что вероятности выпадения его граней будут точно такими же:

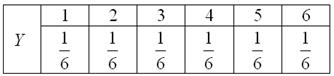
Что мы имеем? Две случайные величины. Но это пока что не система, как, например, не являются системой отдельно взятые диффуры. О системе речь заходит, когда мы рассматриваем эти величины ВМЕСТЕ, например, при подбрасывании костей в игре.

Построим закон распределения вероятностей системы . Так как результат броска одного кубика никак не влияет на количество очков, выпавших на другом кубике, то случайные величины  являются независимыми.

По теореме умножения вероятностей независимых событий, вероятность выпадения любой возможной комбинации очков постоянна и равна . Закон распределения вероятностей можно записать аналитически:

 – вероятность выпадения любой пары , где случайные величины могут принять одно из следующих значений: , .

Но в произвольной задаче вероятности чаще бывают разными, и поэтому на практике широко распространена табличная запись системы. Тот случай, когда копипаст не просто полезен, а очень полезен:

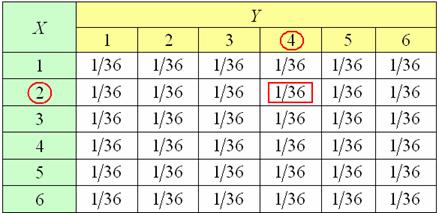
Устройство таблицы очевидно, но на всякий случай я обвёл красным один пример: вероятность того, что случайная величина  примет значение 2 и случайная величина  значение 4 записывается в ячейку, расположенную на пересечении 2-й строки и 4-го столбца.

Обратите внимание, что сумма всех вероятностей равна единице, это означает, что в таблице учтены все возможные исходы (полная группа), и в результате броска двух кубиков достоверно появится одна из 36 пар.

Помимо дискретных, систему могут образовывать и непрерывные случайные величины. За примером далеко ходить не будем: предположим, что мы бросаем игральный кубик в некую цель, например, в коробку. Тогда уместно рассмотреть следующую двумерную случайную величину: , где  – случайное отклонение от цели «по горизонтали» (влево/вправо) и  – случайное отклонение от цели в длину (ближе/дальше).

Кстати, есть ли отличие между понятиями «система двух случайных величин» и «двумерная случайная величина»? – в различных источниках информации используют и тот, и другой термин. С моей точки зрения, отличие есть. Двумерная или большемерная случайная величина, как правило, порождается в результате конкретного испытания, зачастую (но не обязательно) с одним объектом, пожалуйста – тот же бросок кубика в цель. Понятие же системы более формально: один кубик может подбрасывать бабушка на кухне, а другой дедушка в коридоре, или даже ничего не подбрасывать, а совершать прыжки в длину. Но математика-то не запрещает рассмотреть соответствующие СВ единой системой! А психиатрия вообще приветствует.

Пример 1

Независимые случайные величины  принимают только целые значения:

 – от 1 до 13 с равными вероятностями;
 – от 1 до 16 с равными вероятностями.

Найти  – вероятность того, что в очередном испытании сумма появившихся чисел будет меньше шести.

Решение: предложенные случайные величины можно ассоциировать с нестандартными игральными костями, на одной из которых 13, а на другой – 16 граней.

Из условия следует, что:
– вероятность того, что случайная величина  примет какое-либо значение равна  ;
– вероятность того, что случайная величина  примет какое-либо значение равна  .

Так как случайные величины независимы, то по теореме умножения вероятностей независимых событий, вероятность появления любой пары чисел  в очередном испытании постоянна и равна: . Заметьте, что рассмотрение пар уже констатирует тот факт, что мы рассматриваем СИСТЕМУ случайных величин, а не их по отдельности.

Подсчитаем количество пар, соответствующих событию :

сумме  соответствует единственная пара ;

сумме  – пары ;

сумме   – пары

и сумме : .

Итого: 10 нужных пар.

По теореме сложения вероятностей несовместных событий:
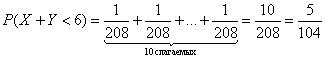 – вероятность того, что сумма появившихся чисел будет меньше шести

Ответ:

Но то, конечно, была разминка:

Пример 2

Две независимые дискретные случайные величины  и  заданы своими законами распределения вероятностей:

Нет, это не опечатка, случайные величины имеют одинаковые законы распределения. Здесь их удобно ассоциировать с двумя одинаковыми и независимо работающими палатами игровыми автоматами, на которых с определенными вероятностями загораются пронумерованные лампочки.

Требуется:

1) Найти закон распределения вероятностей системы случайных величин и вычислить:
 – математическое ожидание случайной величины , при условии, что другая величина приняла значение ;
 – математическое ожидание случайной величины , при условии .

2) Вычислить  – вероятности того, что случайная величина  примет значение из соответствующих двумерных областей.

3) Найти закон распределения вероятностей случайной величины . Вычислить математическое ожидание  и дисперсию .

4) Вычислить

В реальной работе вам может встретиться и то, и другое, и третье и чётвёртое, поэтому разбираемся во всём осознанно и очень внимательно.

Решение:

1) Составим закон распределения вероятностей системы  случайных величин.

 «Иксовые» вероятности будем обозначать как обычно:
,
а к «игрековым» вероятностям добавим «птичку»:

Вычисления стандартно начнём с наименьшего «икса» и «игрека». Найдём  – вероятность того, что случайная величина  примет значение  и случайная величина  значение . По условию, случайные величины независимы, и коль скоро так, то по теореме умножения вероятностей независимых событий:

Найдём  – вероятность того, что :

И так далее. Вычисления удобно проводить на калькуляторе или даже устно, а результаты заносить в таблицу. В качестве ещё одного примера я вычислил и отметил красным цветом вероятность  – того, что случайные величины примут значения :

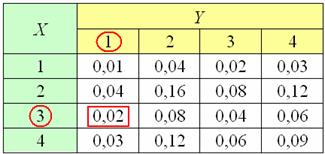
Это и есть закон распределения системы . Не забываем проверить, что сумма всех вероятностей равна единице. Кстати, это ещё не значит, что ошибок нет. Для бОльшей уверенности следует просуммировать вероятности по строкам – в результате должны получиться , т.е. закон распределения случайной величины ; и просуммировать вероятности по столбцам – в результате должны получиться «игрековые» вероятности  величины .

Для системы СВ не вводится понятия «общего» математического ожидания, однако можно подсчитать матожидания условные – при условии, что одна из величин примет или уже приняла некоторое конкретное значение.

Вычислим  – математическое ожидание случайной величины , при условии, что другая величина приняла значение . Так как случайные величины независимы, то распределение случайной величины  не зависит от того, какое значение приняла случайная величина . А значит, при любом возможном значении «игрек» условные математические ожидания:
 – в точности равны матожиданию самой случайной величины .

Логично? Представьте, что на 2-м игровом автомате зажглась лампочка (любая). Ну и что с того? Первый же автомат работает независимо!

Следует отметить, что с зависимыми величинами всё не так, и на следующем уроке мы разберём алгоритм вычисления условного матожидания, который формально пригоден и для независимых величин.

Ну а пока нам достаточно найти математическое ожидание , и заодно сразу вычислим дисперсию, потребуется позже:

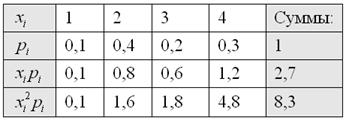
Таким образом:

С вероятностью  аналогично – представьте, что на «иксовом» игровом автомате зажглась лампочка №4. Ну и что? Это никак не повлияло на «игрековый» автомат и его матожидание, поэтому:
 – даже считать не пришлось, т.к. наши случайные величины имеют одинаковые распределения вероятностей.

2) Вычислим вероятность  – того, что случайная величина  примет значение из области, которую задают неравенства в скобках.

По аналогии с одномерным случаем, это можно сделать с помощью функции распределения вероятностей. Но для двумерной СВ составить такую функцию – не то, чтобы сложное, но весьма кропотливое занятие, и поэтому здесь проще просуммировать вероятности, соответствующие условиям . На рисунке ниже я обвёл их красным цветом, и обратите внимание, что в силу строгости неравенства , строку  не следует включать в эту область. Таким образом: – вероятности я привык суммировать по строкам слева направо.

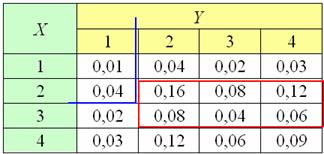
Аналогично, область   отграничена синим цветом, и здесь не следует учитывать значение . В результате:  – вероятность того, что компонента  примет значения, не превосходящее двух, и компонента  – значение, меньшее двух.

И с вероятностью  всё просто. Поскольку на переменную «икс» не наложено никаких ограничений, то она может быть любой, но вот то, что «игрек» окажется больше четырёх – есть событие невозможное. Поэтому .

Точно по такому же принципу вычисляются вероятности и в случае зависимости случайных величин , . Тут разницы нет.

3) Найдем закон распределения вероятностей случайной величины .

Принципиальным отличием от предыдущих пунктов является то, что здесь речь идёт об одномерной случайной величине. Как получаются её значения? С помощью суммирования случайных значений , которые могут принять величины . И нам нужно перебрать все возможные варианты.

Начать удобно с самой маленькой возможной суммы, её образует пара , в результате чего случайная величина «зет» примет значение  с вероятностью:

Может ли сумма равняться трём? Может. Исходу  соответствуют пары . По теоремам умножения вероятностей независимых и сложения несовместных событий:

Сумме  соответствуют пары  и вероятность:

Сумма  тоже возможна, и ей соответствуют 4 пары: . Наверное, вы заметили, что вероятности выпадения всех пар уже подсчитана в первом пункте, и, возможно, на практике вам будет удобнее предварительно составить таблицу распределения вероятностей системы . Но, разумеется, можно обойтись и без неё:

Сумме  соответствуют пары  и вероятность:

Сумме  – пары :

и, наконец, сумме  – последняя возможная пара :
.

Искомый закон распределения  сведём в таблицу и сразу проведём стандартные вычисления для нахождения матожидания и дисперсии:

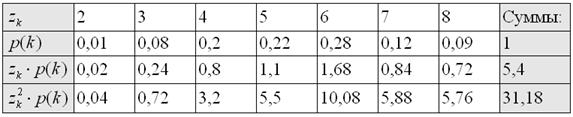
Обязательно контролируем, что , ну и дальнейшее просто:

4) Вычислим

Начнём с . Как можно поступить? Можно составить закон распределения случайной величины  . Паре  соответствует значение , паре  – значение , паре  – значение  и так далее…. И далее напрямую вычислить матожидание. Но есть путь короче.

Для математического ожидания справедливы следующие свойства:

 – математическое ожидание величины, которая принимает единственное значение , равно этому значению. Логично

 – постоянный множитель можно вынести за знак матожидания.

 – это свойство справедливо как для независимых, так и для зависимых случайных величин. И сразу убедимся в справедливости этого факта. В первом пункте мы вычислили , во втором – :
, что и требовалось проверить.

Таким образом:

Но, следует отметить, что вам может быть предложено и «драконовское» задание, а именно, доказать, что . При такой формулировке таки придётся составить закон распределения случайной величины  и вычислить  непосредственно.

Едем дальше. С нахождением  никаких проблем: в первом пункте мы уже вычислили  и по свойствам матожидания:

Энтузиасты могут составить случайную величину , и убедиться в справедливости равенства .

И осталось вычислить .

Для дисперсии справедливы следующие свойства:

 – дисперсия постоянной величины равна нулю.

 – константу можно вынести за знак дисперсии, возведя её в квадрат. Тоже логично: коль скоро, дисперсия – есть квадратичная величина, то при вынесении постоянного множителя, мы должны «расплатиться» возведением его в квадрат.

Для независимых случайных величин справедливо:
, и сразу проверяем: в пункте 1 мы нашли , и в пункте 3 вычислили .

Внимание! Для зависимых величин данное равенство неверно! Но об этом в другой раз.

И из последних двух свойств следует парадоксальное на первый взгляд равенство:
, и тут прямо какой-то закон философии получился – когда из хаоса мы пытаемся вычесть другой хаос, то меры этих хаосов только суммируются.

И настал торжественный момент заключительных вычислений нашей большой задачи:

Готово.

Но готовы ли вы? :) Небольшая задачка для самостоятельного решения:

Пример 3

Две независимые дискретные случайные величины  и  заданы своими законами распределения вероятностей:

Требуется:

1) Найти закон распределения вероятностей системы и вычислить .

Вычисления, кстати, удобно проводить в Экселе – «забиваем» числа и не «забиваем» :)

2) Найти закон распределения вероятностей случайной величины , вычислить и вероятность того, что полученная СВ примет отрицательное значение.

3) Проверить справедливость равенства

В последнем пункте сформулировано ещё одно свойство математического ожидания, которое справедливо только для независимых случайных величин.

Наверное, вы обратили внимание, что во всех задачах этой статьи в условии прямо констатируется независимость случайных величин. Но такого подарка может и не быть, и тогда нам предстоит выполнить самостоятельное исследование. Как его провести? Существуют строгие математические критерии, позволяющие выяснить, зависимы случайные величины или нет, и я приглашаю вас на следующий урок, где мы не только рассмотрим соответствующие примеры, но и узнаем много интересного.

Краткое решение Примера 3:

1) Используя теоремы умножения вероятностей независимых и сложения несовместных событий, составим закон распределения системы :

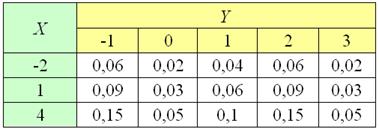
Суммируя вероятности по строкам, убеждаемся, что получается закон распределения случайной величины , и, суммируя вероятности по столбцам, получаем в точности закон распределения .

Вычислим требуемые вероятности:

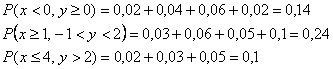
2) Найдём закон распределения случайной величины .

Начнём с наименьшего значения , которое даёт пара . Вероятности появления всех возможных комбинаций уже вычислены в предыдущем пункте:

Произведению  соответствуют пары . По теореме сложения несовместных событий:

Произведению  соответствует пара :

Произведению  – пара :

Произведению  соответствуют пары :

Произведению  – пара :

Произведению  – пары :

Произведению  – пара :

Произведению  – пара :

Произведению  – пара :

и, наконец, произведению  – пара :

Закон распределения случайной величины  сведём в 2 верхние строки расчётной таблицы, не забывая проконтролировать, что :

Математическое ожидание: , дисперсия:

 – вероятность того, что случайная величина  примет отрицательное значение.

3) Покажем справедливость равенства .

 – вычислено в предыдущем пункте.

Вычислим матожидания исходных случайных величин:

Таким образом:

 – получено верное равенство, что и требовалось проверить.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте