Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

5. Размах вариации. Среднее линейное отклонение.
Генеральная и выборочная дисперсия

На предыдущем уроке по математической статистике мы изучили центральные показатели статистической совокупности, а именно моду, медиану, среднюю, и теперь переходим к показателям вариации. Они показывают, КАК варьируются статистические данные, а именно – насколько далеко «разбросаны» варианты относительно средних значений, да и просто друг от друга. В данной статье будут рассмотрены самые популярные показатели, и для опытных читателей сразу оглавление:

• Размах вариации
• Среднее линейное (абсолютное) отклонение
• Генеральная и выборочная дисперсия, тут же исправленная выборочная дисперсия

и, чтобы не «лепить» километровую простыню, разделю материал на две веб страницы:

• Во второй части будет формула для вычисления дисперсии, среднее квадратическое (стандартное) отклонение и коэффициент вариации.

Итак, прямо сейчас мы сформулируем определения этих показателей, узнаем соответствующие формулы и, конечно, потренируемся в конкретных вычислениях. Да не просто в конкретных, а в рациональных.

Но прежде систематизируем информацию о том, какие статистические данные могут оказаться в нашем распоряжении:

– они могут быть первичными (не обработанными), грубо говоря – это неупорядоченный список чисел, либо вторичными – это уже сформированный дискретный (Урок 2) или интервальный вариационный ряд (Урок 3).

– рассматриваемая статистическая совокупность может быть генеральной либо выборочной, и чаще, конечно, перед нами выборка.

…что-то не понятно по терминам? Срочно изучать основы предмета (Урок 1)! – это быстро и интересно, ну а я, сколько нужно, вас тут подожду :)

Размах вариации

Он уже встречался. Это разность между самым большим и самым малым значением статической совокупности:

при этом не имеет значения, генеральная ли нам дана совокупность или выборочная, сгруппированы ли данные или нет.

Очевидно, что все варианты  исследуемой совокупности (той или иной) заключены в отрезке , а размах  – есть не что иное, как его длина.

Такой вот простой, надёжный и понятный показатель. Но, несмотря на его элементарность, рассмотрим технику вычисления, и, конечно, это отличный повод размяться:

Пример 12

Дана статистическая совокупность
15, 17, 13, 10, 21, 17, 23, 9, 14, 19

Найти размах вариации

Решить задачу можно несколькими способами.

Способ первый, суровый – продолжаю вас готовить к борьбе с киборгами :)) Это когда под рукой нет вычислительной техники. Или когда она есть, но вы сами понимаете, как важно «прокачать» свои человеческие способности.

Если чисел не так много (наш случай), то максимальное и минимальное значения легко углядеть устно:  и размах равен:  единиц.

Если чисел больше (20-30 и даже больше), то надёжен следующий алгоритм:

1) Ищем минимальное значение. Сначала самым маленьким будет первое число: 15. Второе число (17) больше, и поэтому его пропускаем. Третье число (13) меньше, чем 15, и теперь 13 – самое малое число. И так далее, пока не закончится список.

2) Ищем максимальное значение. Сначала самым большим будет первое число: 15. Второе число (17) больше и теперь оно становится самым большим. И так далее – до конца списка.

Способ второй, более быстрый (обычно). Использование программного обеспечения, при этом числа можно просто отсортировать (по возрастанию либо убыванию) или использовать специальные функции:

Задание 6

Найти максимальное и минимальное значения в Экселе – данные уже там, данные вас ждут!

…отлично, молодцы!

Запишем ответ  ед. и с нетерпением перейдём к другим показателям, которые характеризуют степень рассеяния вариант относительно центра совокупности, прежде всего, относительно средней.

О смысле и важности этих показателей я рассказал в курсе теории вероятностей (статья о дисперсии дискретной случайной величины), но коротко повторю и сейчас. Рассмотрим двух студентов, каждый из которых в среднем учится на 3,5 балла. Но есть один нюанс. Один стабильно получает тройки-четвёрки, а другой то пятёрки, то двойки. И поэтому важно знать меру рассеяния оценок относительно средней величины. Чем она меньше – тем стабильнее учится студент.

Эту меру можно оценить следующим образом: из каждой оценки  (пусть их будет  штук) вычитаем среднее значение .   Величина  называется отклонением (значения ) от средней.

Теперь эти отклонения нужно просуммировать, но тут появляется проблема: среди разностей  есть как положительные, так и отрицательные, и при их суммировании будет происходить взаимоуничтожение отклонений. Более того, итоговая сумма равна нулю: , и мы не получаем желаемого результата.

Вопрос можно решить с помощью модуля, который уничтожает минусы: , после чего осталось разделить сумму на объём совокупности  и получить:

среднее линейное отклонение

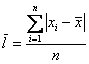 – есть среднее арифметическое абсолютных отклонений всех значений статистической совокупности от средней. Это формула для несгруппированных статистических данных.

Если же в нашем распоряжении есть сформированный дискретный либо интервальный вариационный ряд, то формула будет такой:

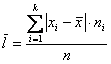, где  – варианты (для дискретного ряда) либо середины частичных интервалов (для интервального ряда), а  – соответствующие частоты.

Напоминаю, что маленькая буква  обычно используется для выборочной совокупности, а большая  – для генеральной:  – объём ген. совокупности,   – частоты.

И начнём мы с малого:

Пример 13

В результате 10 независимых измерений некоторой величины, выполненных с одинаковой точностью, получены опытные данные, которые представлены в таблице:

Требуется вычислить среднее линейное отклонение

Решение: очевидно, что перед нами первичные данные и выборочная совокупность (теоретически измерений можно провести бесконечно много). На первом шаге вычислим выборочную среднюю:

Теперь находим модули отклонений от средней:

…
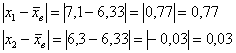
и так далее до:

Вычисления удобно проводить на калькуляторе или в Экселе, а результаты заносить в таблицу:

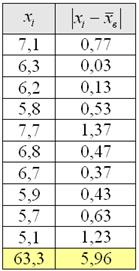
На завершающем этапе рассчитываем сумму модулей:
 и среднее линейное отклонение:
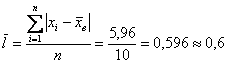 ед. – оно означает, что измеренные значения  в среднем отличаются от  примерно на 0,6 ед.

Но помимо этого, для оценки рассеяния вариант относительно средней существует более совершенный и распространённый подход. Он состоит в том, чтобы использовать не модули, а возведение отклонений в квадрат:  (чтобы ликвидировать встречающиеся отрицательные значения).

Генеральная и выборочная дисперсия

Дисперсия с латыни так и переводится – рассеяние.

…не сломать бы язык :) …так… Выборочная дисперсия  – это среднее арифметическое квадратов отклонений всех вариант выборки от её средней:
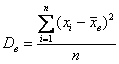 – для несгруппированных данных, и:

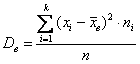 – для сформированного вариационного ряда, где  – кратные (одинаковые по значению) варианты в дискретном случае либо середины частичных интервалов – в интервальном, и  – соответствующие частоты.

Еще раз не спеша и ОСМЫСЛЕННО прочитайте определение и выполните

Задание:

Сформулировать и записать (на бумагу!) определение генеральной дисперсии и соответствующие формулы.

Свериться можно, как обычно, в конце урока.

После чего следует

продолжение Примера 13

По тем же исходным данным вычислить выборочную дисперсию

Без проблем. Вместо модулей рассчитываем квадраты отклонений:

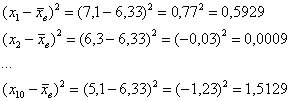
заполняем табличку:

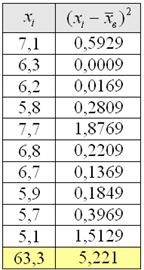
и порядок:
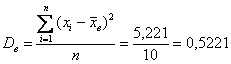 квадратных (!) единиц  – коль скоро, мы возводили в квадрат. И, чтобы вернуться в размерность задачи, из дисперсии следует извлечь корень. Но мы не будем торопить события, лучше посмотрим, как выполнять вычисления в Экселе:

Ответ:

Разобранная задача де-факто встречается в лабораторных работах по физике (да и не только) – когда некоторая величина замеряется раз 10 и затем рассчитывается среднее значение.

А теперь представьте, что вся ваша группа выполняет лабу по физике, и каждый провёл по 10 испытаний в схожих условиях. Очевидно, что у всех получились несколько разные выборочные значения , но все они без какой-либо закономерности (в общем случае) будут варьироваться вокруг истинного значения показателя  (роль генеральной средней может играть некий теоретический эталон). Это свойство (отсутствие закономерности) называется несмещённостью оценки генеральной средней, и справедливо оно, как мы увидим ниже, не для всех показателей.

Теперь пару ласковых об отклонениях. В чём их смысл? Всё просто: у кого эти показатели ниже, тот качественнее проводит опыты (плавнее выполняет действия, точнее снимает показания с приборов, засекает время и т.п.). В идеале эти отклонения равны нулю, но это только в идеале – сам эмпиризм ситуации порождает генеральное линейное отклонение  и генеральную дисперсию, которые обусловлены человеческим фактором, погрешностью приборов и так далее – вплоть до магнитных бурь.

В случае с полученными линейными отклонениями  – всё то же самое, они будут безо всякой закономерности варьироваться вокруг генерального значения . Но вот с дисперсией всё не так. Полученные значения выборочной дисперсии  будут давать систематически заниженную оценку генеральной дисперсии . И поэтому выборочную дисперсию следует «поправить» по формуле:

  – желающие могут найти обоснование этого факта и этой формулы в специализированной литературе по математической статистике.

Показатель  так и называется – исправленная выборочная дисперсия, и вот она уже является несмещённой оценкой генеральной дисперсии.

Таким образом, каждый студент должен поправить свою дисперсию, в частности, для Примера 13:

Следует отметить, что для большой выборки (от 100 и даже от 30 вариант) этой поправкой можно пренебречь, так как при  дробь  стремится к единице и .

И иногда дисперсию можно вовсе не поправлять. Так, в разобранном примере от нас требовалось просто вычислить выборочную дисперсию и всё. А если хочется что-то додумать, то пусть этого захочет преподаватель :) Но вот если дисперсия будет «участвовать» в дальнейших действиях, то, конечно, приводим её к виду . 

Более того, встречаются задачи, где вообще не понятно – выборочная ли дана совокупность или генеральная, и тогда разумно проявить аккуратность и использовать обозначения без подстрочных индексов, в частности,  и .

Теперь случай, когда дан готовый вариационный ряд. У меня опять есть подходящая советская задача про телефонную станцию, но я скорректирую условие в соответствии с современными реалиями:

Пример 14

В результате выборочного исследования звонков, статистик МТС получил следующие данные (за некоторый временной промежуток):

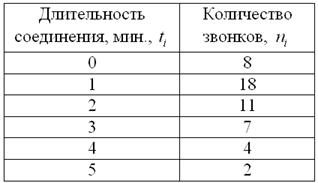
…у ОпСоСов, как известно, своя статистика – с округлением до ближайшей целой минуты :), впрочем, это тоже устареет…, как метко заметил современник, дети дружно играли во дворе – каждый в своём смартфоне(

Найти размах вариации, среднее линейное отклонение и выборочную дисперсию. Дать несмещённую оценку генеральной дисперсии и пояснить, что это означает.

Задание 7

Решить данную задачу в Экселе (данные и гайд уже там) либо на бумаге с помощью калькулятора.

Краткое решение и ответ совсем близко, поскольку 1-я часть урока подошла к концу, и я жду вас во 2-й части, где мы рассмотрим формулу для вычисления дисперсии, среднее квадратическое отклонение и коэффициент вариации.

Решения и ответы:

Задание. Генеральная дисперсия  – это среднее арифметическое квадратов отклонений всех вариант генеральной совокупности от её средней:
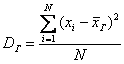, где  – объём генеральной совокупности.
Для сформированного вариационного ряда формула принимает вид:
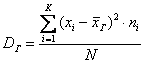, где  – либо варианты дискретного ряда, либо середины частичных интервалов интервального ряда, а  – соответствующие частоты.

Пример 14. Решение: найдём размах вариации:  мин.

Вычислим объём совокупности , произведения , их сумму и выборочную среднюю  мин.
Рассчитаем , произведения   и их суммы:

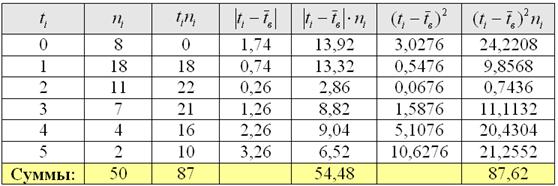
Среднее линейное отклонение:
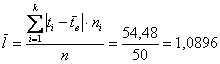 мин.
Выборочная дисперсия:
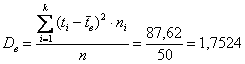 мин. в квадрате.
Несмещённой оценкой генеральной дисперсии является исправленная выборочная дисперсия:
 мин. в квадрате.
Несмещённость означает, что если в схожих условиях проводить аналогичные выборки, то полученные значения  будут безо всякой закономерности варьироваться вокруг генерального значения .

Ответ:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте