


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Криволинейный интеграл по замкнутому контуру. Формула Грина.
Работа векторного поля
Ничего страшного в этом заголовке нет – по существу, мы продолжаем решать криволинейные интегралы 2-го рода. Новизна будет состоять в особенности пути интегрирования, а именно в его замкнутости. Наверное, всем интуитивно понятно, что это значит – встаньте с места и прогуляйтесь, как вам захочется. После чего вернитесь в исходную точку. Это и есть замкнутый контур. …Вот видите, как он полезен для разминки затекших от учёбы членов!
В рамках этой статьи я рассмотрю элементарные «маршруты» без самопересечений, такие как окружность, треугольник, квадрат и т.д. Криволинейный интеграл по замкнутому контуру ![]() так и обозначают – с символической окружностью посередине:
так и обозначают – с символической окружностью посередине:
![]()
Нередко на ней рисуют стрелочку, указывая направление движения:
– против часовой стрелки;
– либо по часовой стрелке.
На практике чаще всего встречается первый вариант, который принято называть положительным направлением обхода контура.
Впрочем, чтобы послать по контуру – стрелка не обязательна:)
Пример 10
Да, пример уже десятый! – кто не успел, тот навёрстывает упущенное!
Вычислить интеграл ![]() по контуру
по контуру ![]() , ограниченному линиями
, ограниченному линиями ![]() . Интегрировать против часовой стрелки. Выполнить чертёж.
. Интегрировать против часовой стрелки. Выполнить чертёж.
Решение: Слушаемся и повинуемся:)
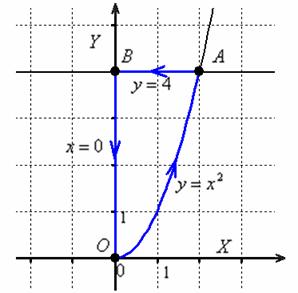
Напоминаю, что для криволинейного интеграла 2-го рода принципиально важнО направление интегрирования, и поэтому на чертеже крайне желательно проставлять стрелочки.
В силу свойства аддитивности, криволинейный интеграл по контуру ![]() можно представить в виде суммы трёх интегралов:
можно представить в виде суммы трёх интегралов:
![]()
1) Вычислим интеграл по дуге ![]() параболы. Если
параболы. Если ![]() , то:
, то:
![]()
В соответствии с направлением, ![]() изменяется от 0 до 2:
изменяется от 0 до 2:
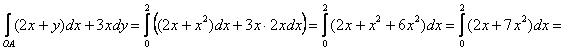
![]() – именно так, в виде обыкновенной неправильной дроби.
– именно так, в виде обыкновенной неправильной дроби.
Желающие могут выполнить проверку: выразить нужный кусок параболы: ![]() , найти
, найти ![]() и проинтегрировать по «игрек» от 0 до 4.
и проинтегрировать по «игрек» от 0 до 4.
2) Вычислим интеграл по отрезку ![]() прямой
прямой ![]() . С дифференциалом тут всё просто:
. С дифференциалом тут всё просто:
![]() , а вот с пределами интегрирования не очень – интегрировать нужно строго по заданному направлению, то есть от 2 до 0 (см. чертёж):
, а вот с пределами интегрирования не очень – интегрировать нужно строго по заданному направлению, то есть от 2 до 0 (см. чертёж):
![]()
3) И, наконец, интеграл по фрагменту ![]() оси ординат. Если
оси ординат. Если ![]() , то, понятно, что
, то, понятно, что ![]() , и «игрек» изменяется (внимание!) от 4 до 0:
, и «игрек» изменяется (внимание!) от 4 до 0:
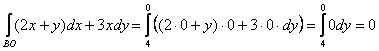
Таким образом, интеграл по контуру:
![]()
Ответ: ![]()
Очевидно, что если контур обойти по часовой стрелке, то получится противоположное значение: ![]() .
.
Другой очевидный факт состоит в том, что если мы «выйдем» из любой другой точки контура и совершим «оборот» (в том или ином направлении), то значение интеграла не изменится.
Что можно сказать по поводу выполненного задания? Решение хорошее, решение логичное, однако у него есть существенный недостаток. Оно длинное. Но это не беда! Если нет беды с двойными интегралами =) Для простых контуров существует
формула Грина – Остроградского
Или, как её чаще называют – просто формула Грина, которую обычно записывают для положительного направления обхода контура:
![]() , где
, где ![]() – замкнутая область, ограниченная контуром
– замкнутая область, ограниченная контуром ![]() .
.
Примечание: функции ![]() должны быть определены и непрерывны в области
должны быть определены и непрерывны в области ![]() и, кроме того, иметь в ней непрерывные частные производные
и, кроме того, иметь в ней непрерывные частные производные ![]() .
.
Решим наш интеграл ![]() по формуле Грина. Сначала найдём частные производные:
по формуле Грина. Сначала найдём частные производные:
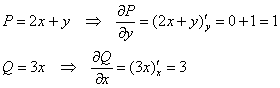
И, выбирая привычный порядок обхода области ![]() , получаем:
, получаем:
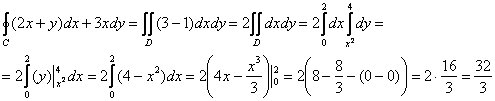
Как видите, решение сильно сократилось, а иногда оно сокращается просто фантастически!
Пример 11
Вычислить криволинейный интеграл ![]() по окружности
по окружности ![]() :
:
а) непосредственно, б) по формуле Грина.
Решение: естественно, здесь не нужно мучиться с дугами ![]() (хотя можно) – гораздо проще представить уравнение окружности
(хотя можно) – гораздо проще представить уравнение окружности ![]() в параметрической форме, которая уже неоднократно встречалась ранее:
в параметрической форме, которая уже неоднократно встречалась ранее:
![]()
В условии ничего не сказано о направлении обхода контура, но пункт «бэ» толсто намекает, что лучше двигаться против часовой стрелки. К тому же, традиционное возрастание параметра ![]() как раз и обеспечивает «виток» именно в этом направлении:
как раз и обеспечивает «виток» именно в этом направлении:
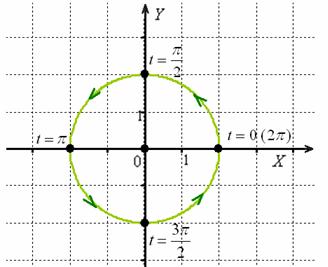
Чертёж, к слову, был вовсе не обязателен, и ввиду простоты контура можно было обойтись и без него. Однако не в этот раз – пожалуйста, ХОРОШО запечатлейте эту картинку в своём сознании!
а) Вычислим криволинейный интеграл непосредственно. Алгоритм решения обычный – «начинку» интеграла нужно «заправить» буквой «тэ». Найдём дифференциалы:
![]()
и подставим ![]() в подынтегральное выражение. Чтобы не запутаться рекомендую оформлять преобразования «простынёй»:
в подынтегральное выражение. Чтобы не запутаться рекомендую оформлять преобразования «простынёй»:
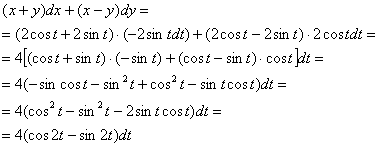
…надеюсь, использованные тригонометрические формулы вы не забудете в любом состоянии =)
Таким образом, криволинейный интеграл:
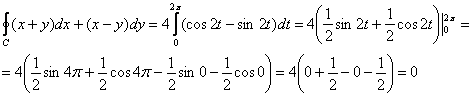
б) Вычислим интеграл по формуле Грина:
![]() , где
, где ![]() – замкнутая область, ограниченная контуром
– замкнутая область, ограниченная контуром ![]() . В данном случае это круг радиуса 2. Но возиться с полуокружностями не придётся и здесь! – поскольку:
. В данном случае это круг радиуса 2. Но возиться с полуокружностями не придётся и здесь! – поскольку:
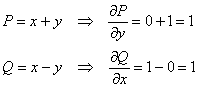
и сбылась мечта тунеядца:)
![]()
Ответ: ![]()
И это не только приятный, но ещё и крайне интересный случай. Если криволинейный интеграл по замкнутому контуру равен нулю, то речь заходит об очень крутом свойстве! Даже нескольких свойствах. Должен предупредить, что сейчас я буду вольно пересказывать теоремы математического анализа, и если вы учитесь основательно, то обязательно загляните в 3-й том Фихтенгольца (например).
Рассмотрим две произвольные точки области ![]() (круга). Очевидно, что их можно соединить бесчисленным количеством кусочно-гладких маршрутов, не выходящих за пределы области. Так вот – какой бы из этих путей мы ни выбрали, то во всех случаях криволинейный интеграл будет равняться одному и тому же значению!
(круга). Очевидно, что их можно соединить бесчисленным количеством кусочно-гладких маршрутов, не выходящих за пределы области. Так вот – какой бы из этих путей мы ни выбрали, то во всех случаях криволинейный интеграл будет равняться одному и тому же значению!
Но это только «вершки». Поскольку функции ![]() непрерывны во всех точках плоскости
непрерывны во всех точках плоскости ![]() , то то же самое справедливо и для любых двух точек плоскости! То есть, мы можем зафиксировать вообще любые две точки (какие понравятся) и составить бесконечно много кусочно-гладких маршрутов между ними. И криволинейные интегралы по всем этим маршрутам будут равны одному и тому же числу!
, то то же самое справедливо и для любых двух точек плоскости! То есть, мы можем зафиксировать вообще любые две точки (какие понравятся) и составить бесконечно много кусочно-гладких маршрутов между ними. И криволинейные интегралы по всем этим маршрутам будут равны одному и тому же числу!
В таких случаях говорят, что криволинейный интеграл не зависит от пути интегрирования, а зависит он только от начальной и конечной точки.
Вернёмся к только что разобранному примеру и рассмотрим произвольную пару точек, лежащую внутри круга ![]() – проще всего взять точки
– проще всего взять точки ![]() . Теперь вычислим криволинейный интеграл следующими способами:
. Теперь вычислим криволинейный интеграл следующими способами:
1) По отрезку ![]() прямой
прямой ![]() . Тут всё элементарно:
. Тут всё элементарно: ![]() и:
и:
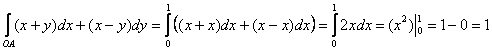
2) По дуге ![]() параболы
параболы ![]() . В этом случае
. В этом случае ![]() и:
и:
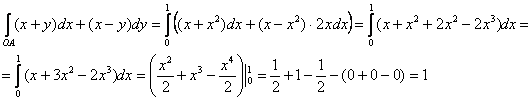
Самостоятельно вычислите этот же интеграл по дуге ![]() кубической параболы
кубической параболы ![]() . Получится единица.
. Получится единица.
Или по какой-нибудь простенькой ломаной, например, по ломаной ![]() , где
, где ![]() . Тоже получится единица! Возьмите точку
. Тоже получится единица! Возьмите точку ![]() вне круга и снова получИте свою законную единицу!
вне круга и снова получИте свою законную единицу!
И вообще – если выбрать любой кусочно-гладкий путь от точки ![]() до точки
до точки ![]() , то криволинейный интеграл во всех случаях будет равняться единице! Сколь бы длинным и запутанным ни был маршрут в плоскости
, то криволинейный интеграл во всех случаях будет равняться единице! Сколь бы длинным и запутанным ни был маршрут в плоскости ![]() , сколько бы он не самопересекался (да, даже так).
, сколько бы он не самопересекался (да, даже так).
Иными словами, значение криволинейного интеграла не зависит от пути интегрирования. И, как я уже отметил выше, в нашем примере можно взять вообще две любые точки плоскости ![]() , и криволинейный интеграл не будет зависеть от пути интегрирования.
, и криволинейный интеграл не будет зависеть от пути интегрирования.
Более того, если рассмотреть произвольный замкнутый кусочно-гладкий контур ![]() в плоскости
в плоскости ![]() , то интеграл по любому такому контуру будет равен нулю:
, то интеграл по любому такому контуру будет равен нулю: ![]() .
.
И всё это последовало из того, что мы получили ноль хоть по какому-то замкнутому контуру (по окружности в нашем примере), а также из того факта, что функции ![]() непрерывны всюду.
непрерывны всюду.
Но открытия только начинаются!
Если ![]() , то подынтегральное выражение является полным дифференциалом некоторой функции двух переменных
, то подынтегральное выражение является полным дифференциалом некоторой функции двух переменных ![]() . Данная функция называется потенциальной или просто потенциалом. Как её найти? Очень просто. Нужно решить
. Данная функция называется потенциальной или просто потенциалом. Как её найти? Очень просто. Нужно решить ![]() – дифференциальное уравнение в полных дифференциалах.
– дифференциальное уравнение в полных дифференциалах.
Для «начинки» нашего нулевого интеграла ![]() таковой функцией является:
таковой функцией является: ![]()
И в самом деле, её полный дифференциал:
![]() – в точности подынтегральное выражение.
– в точности подынтегральное выражение.
Ну и, наверное, все уже поняли, что равенство ![]() , которое обеспечивает ноль в формуле Грина, есть не что иное, как равенство смешанных производных 2-го порядка.
, которое обеспечивает ноль в формуле Грина, есть не что иное, как равенство смешанных производных 2-го порядка.
Более того, для любых двух точек ![]() и
и ![]() области
области ![]() (и вообще всей плоскости
(и вообще всей плоскости ![]() ) криволинейный интеграл
) криволинейный интеграл ![]() – равен постоянной величине, которая не зависит от пути интегрирования, а зависит только от начальной и конечной точки.
– равен постоянной величине, которая не зависит от пути интегрирования, а зависит только от начальной и конечной точки.
Так, в нашем примере с точками ![]() было совсем не обязательно перебирать множество маршрутов – достаточно найти потенциальную функцию
было совсем не обязательно перебирать множество маршрутов – достаточно найти потенциальную функцию ![]() (решив ДУ в полных дифференциалах) и вычислить криволинейный интеграл по формуле:
(решив ДУ в полных дифференциалах) и вычислить криволинейный интеграл по формуле:
![]()
Разность ![]() называют разностью потенциалов, и я так вижу, у физиков уже появился здоровый блеск в глазах =) Поэтому не буду томить вас ожиданием и сразу перейду к изложению «главного» физического смысла криволинейного интеграла 2-го рода:
называют разностью потенциалов, и я так вижу, у физиков уже появился здоровый блеск в глазах =) Поэтому не буду томить вас ожиданием и сразу перейду к изложению «главного» физического смысла криволинейного интеграла 2-го рода:
Работа векторного поля
Пусть материальная точка под воздействием силы векторного поля ![]() совершает движение в плоскости и проходит путь
совершает движение в плоскости и проходит путь ![]() . Тогда работа векторного поля по перемещению этой точки определяется формулой:
. Тогда работа векторного поля по перемещению этой точки определяется формулой: ![]() . Данная величина стандартно измеряется в Джоулях, но в математических задачах размерность почти никогда не указывается, и я тоже буду придерживаться этого стиля.
. Данная величина стандартно измеряется в Джоулях, но в математических задачах размерность почти никогда не указывается, и я тоже буду придерживаться этого стиля.
Давайте разбираться. Приведу не совсем строгий, но зато вполне понятный пример: представьте, что у вас на столе лежит плоский и достаточно тонкий магнит. Из жизненного опыта все хорошо знают, что чем ближе поднести к нему какую-нибудь железку, тем сильнее она будет притягиваться. В физике это «сильнее» измеряется векторной величиной под названием напряжённость магнитного поля:
– каждой точке ![]() поверхности стола ставится в соответствие несвободный вектор
поверхности стола ставится в соответствие несвободный вектор ![]() , указывающий направление действия силы (магнитного поля) и её величину в данной точке (чем ближе к магниту, тем длиннее вектор). Множество этих векторов (рассматриваем только плоскость) образует двумерное векторное поле. Такое поле можно формализовать векторной функцией скалярного аргумента:
, указывающий направление действия силы (магнитного поля) и её величину в данной точке (чем ближе к магниту, тем длиннее вектор). Множество этих векторов (рассматриваем только плоскость) образует двумерное векторное поле. Такое поле можно формализовать векторной функцией скалярного аргумента:
![]()
И в самом деле, если мы начнём подставлять координаты ![]() различных точек (скалярные аргументы), то «на выходе» будем получать различные векторы
различных точек (скалярные аргументы), то «на выходе» будем получать различные векторы ![]() . Чтобы было понятнее, приведу конкретный пример:
. Чтобы было понятнее, приведу конкретный пример: ![]() – найдём значение этой функции, например, в точке
– найдём значение этой функции, например, в точке ![]() :
:
![]() – в результате получен вектор, который, повторюсь, привязан к точке
– в результате получен вектор, который, повторюсь, привязан к точке ![]() и свободному перемещению не подлежит! Догадайтесь с одного раза, почему.
и свободному перемещению не подлежит! Догадайтесь с одного раза, почему.
Теперь недалеко от магнита бросим железную пылинку, которая под действием силы магнитного поля проделает путь ![]() (за некоторое время). Таким образом, данное векторное поле совершило работу
(за некоторое время). Таким образом, данное векторное поле совершило работу ![]() по перемещению этой пылинки. А вы как думали? – работают даже магниты! Всегда вспоминайте об этом, когда устанете от какой-нибудь работы =)
по перемещению этой пылинки. А вы как думали? – работают даже магниты! Всегда вспоминайте об этом, когда устанете от какой-нибудь работы =)
И совсем понятный пример находится у многих под рукой, а именно компьютерная мышка – переместите её по произвольной траектории. Сила ваших мускулов совершила работу по перемещению мыши. Следует однако отметить, что обывательское и физическое понимание работы отличаются, и к этому вопросу я вернусь буквально через несколько строк:
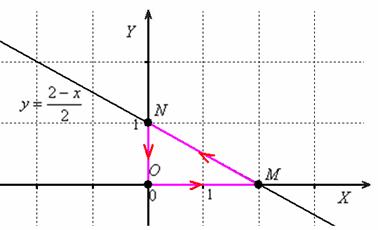
Пример 12
Вычислить непосредственно и с помощью формулы Грина работу векторного поля ![]() по контуру, представляющему собой треугольник с вершинами в начале координат и точках
по контуру, представляющему собой треугольник с вершинами в начале координат и точках ![]() ,
, ![]() (контур интегрирования следует обходить против движения часовой стрелки).
(контур интегрирования следует обходить против движения часовой стрелки).
Краткое решение и ответ в конце урока. И не такое оно, между прочим, простое, как может показаться ;-)
Не удивляйтесь, если работа будет получаться отрицательной – знаки «плюс» и «минус» указывают направление действия силы. Так, если вы переместите мышь вправо, то, условно говоря, совершите работу ![]() . Теперь возвращаем её в исходную точку (не обязательно по той же траектории) и предполагаем, что усилий затрачено столько же. Тот факт, что сила ваших мускулов работала в противоположном направлении, и выражается знаком «минус»:
. Теперь возвращаем её в исходную точку (не обязательно по той же траектории) и предполагаем, что усилий затрачено столько же. Тот факт, что сила ваших мускулов работала в противоположном направлении, и выражается знаком «минус»: ![]() .
.
Вы поработали? Безусловно. Хотя и не перетрудились =) Но с точки зрения физики работы не совершено! И действительно, работа по замкнутому контуру составила ![]() . Вот так вот своими руками вы смоделировали особый вид поля!
. Вот так вот своими руками вы смоделировали особый вид поля!
Если интеграл по замкнутому контуру равен нулю, то соответствующее векторное поле называют потенциальным. Проверим, будет ли оно таковым в Примере 12:
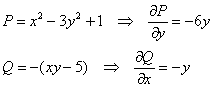
![]() , следовательно, потенциальной функции не существует и поле
, следовательно, потенциальной функции не существует и поле ![]() не потенциально. Поэтому можно сразу сказать, что
не потенциально. Поэтому можно сразу сказать, что ![]()
Кстати, такое задание иногда встречается: проверить будет ли данное поле потенциальным и если да, то найти его потенциал. Напоминаю, что для нахождения потенциальной функции нужно решить дифференциальное уравнение в полных дифференциалах. Что делать в пространственном случае – смотрите в статье о теории поля.
И в заключение урока мы как раз немного поговорим
о криволинейных интегралах в пространстве
А почему нет? Никто же не запрещает интегрировать по пространственным кривым. Наоборот – все только разрешают =)
На самом деле я мог бы начать и с них, но, во-первых, такие задачи значительно реже встречаются на практике, и, во-вторых, возникла бы неслабая путаница.
Пространственная кривая, как правило, задаётся параметрическими уравнениями ![]() , и по большому счёту новизна состоит в дополнительной координате.
, и по большому счёту новизна состоит в дополнительной координате.
Так, например, криволинейный интеграл 1-го рода, рассчитывается по формуле:
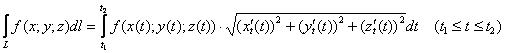 , и его физический смысл – это масса пространственной линии
, и его физический смысл – это масса пространственной линии ![]() , где
, где ![]() – функция её плотности.
– функция её плотности.
Криволинейный интеграл 2-го рода запишется в виде:
![]() , и, наверное, вы уже догадываетесь, как его решать. Осталось подтвердить свою догадку решением заключительного примера:
, и, наверное, вы уже догадываетесь, как его решать. Осталось подтвердить свою догадку решением заключительного примера:
Пример 13
Вычислить криволинейный интеграл ![]() , где
, где ![]() – первый виток винтовой линии
– первый виток винтовой линии ![]() .
.
Тот, кто хорошо разобрался с параметрическими уравнениями окружности, легко представит эту линию в уме. Впрочем, информацию не сложнее разыскать в Сети.
Аналогично – предложенный криволинейный интеграл можно интерпретировать, как работу трёхмерного векторного поля ![]() по перемещению материальной частицы вдоль пространственной кривой
по перемещению материальной частицы вдоль пространственной кривой ![]() .
.
Не так давно я оговорился, что работа – есть «главный» физический смысл криволинейного интеграла. Здесь я имел в виду, что задача на работу силы – самая известная. Криволинейные интегралы находят широчайшее применение в физике, и с помощью них можно подсчитать много других величин.
И, к слову, термин «поле» – он не физический, а относится именно к математике. Силовые же физические поля – лишь частные примеры. Обязательно ознакомьтесь с увлекательной теорией поля!
Но это после того, как будет покончено с интегралами. Ещё существуют поверхностные. Впрочем, уж они-то после всех испытаний – так, ерунда =)
Желаю успехов!
Решения и ответы:
Пример 12: Решение: выполним чертёж:
I. Вычислим работу векторного поля непосредственно:
![]()
1) На отрезке ![]() :
: ![]() ,
, ![]() изменяется от 0 до 2:
изменяется от 0 до 2:
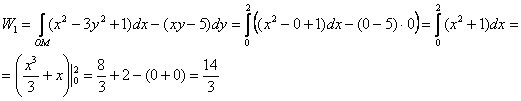
2) Составим уравнение, содержащее отрезок ![]() , по двум точкам
, по двум точкам ![]() :
:
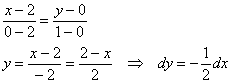
![]() изменяется от 2 до 0:
изменяется от 2 до 0:

3) На отрезке ![]() :
: ![]() ,
, ![]() изменяется от 1 до 0:
изменяется от 1 до 0:
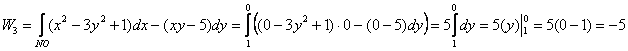
Таким образом, работа векторного поля по данному контуру:
![]()
II. Вычислим криволинейный интеграл по формуле Грина:
![]()
В данном случае:
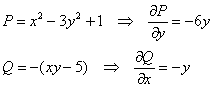
Таким образом:

Ответ: ![]()
Пример 13: Решение: найдём дифференциалы:
![]() и подставим их вместе с
и подставим их вместе с ![]() в подынтегральное выражение:
в подынтегральное выражение:
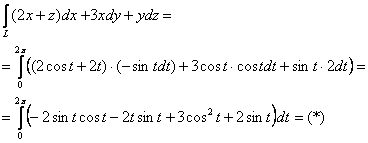
Для удобства интегралы вычислим по отдельности:
1) 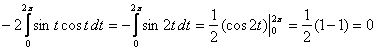
2) 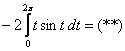
Интегрируем по частям:
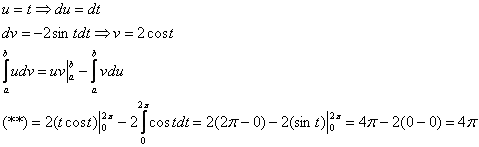
3) 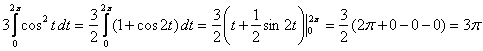
4) 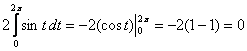
Таким образом:
![]()
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright