


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Непрерывность функции двух переменных
После изучения предела функции двух переменных настало время рассмотреть тесно связанное с ним понятие, а именно – непрерывность. Уже из первой статьи о функциях нескольких переменных становится интуитивно понятно, что такое непрерывность функции двух переменных. Потому что всё просто и логично – ведь если есть некая поверхность в пространстве, заданная функцией ![]() или уравнением
или уравнением ![]() , то вполне естественно, что она может быть как «единым лоскутом», так и терпеть различные разрывы. И сегодня мы загоним эти обывательские представления в жёсткие рамки высшей математики. Но, прежде чем вплотную заняться данными вопросами, рекомендую освежить в памяти непрерывность функции одной переменной, поскольку многие термины, да и сам подход к исследованию функции на непрерывность будут очень и очень похожи.
, то вполне естественно, что она может быть как «единым лоскутом», так и терпеть различные разрывы. И сегодня мы загоним эти обывательские представления в жёсткие рамки высшей математики. Но, прежде чем вплотную заняться данными вопросами, рекомендую освежить в памяти непрерывность функции одной переменной, поскольку многие термины, да и сам подход к исследованию функции на непрерывность будут очень и очень похожи.
Первое, что бросается в глаза при изучении темы – это величайшее многообразие поверхностей и их разрывов, причём некоторые из них напоминают целое произведение искусства, да такое, что иной художник и рядом не курил. В отличие от графиков функций одной переменной, поверхность может терпеть разрыв не только в отдельно взятых точках, но и вдоль целых линий; она может «стягиваться», «извиваться», «идти волнами» и принимать самые необычные формы. Пожалуйста:
И это ещё довольно таки простая функция. Однако уроки рисования проходят в соседней аудитории, и поэтому мы не будем углубляться в художественные тонкости. Да-да, правильно предчувствуете – нас ждут теоретические выкладки и бородатые примеры =)
В теории существует несколько определений непрерывности функции в точке, но для практических целей нашего занятия я сформулирую лишь «прикладной» вариант:
функция ![]() непрерывна в точке
непрерывна в точке ![]() , если её общий предел в этой точке равен значению данной функции в данной точке:
, если её общий предел в этой точке равен значению данной функции в данной точке:
![]()
Откуда следует хорошо знакомый алгоритм проверки на непрерывность:
1) Определена ли функция в точке ![]() ? Если нет, то сразу делаем вывод о том, что функция терпит разрыв в данной точке.
? Если нет, то сразу делаем вывод о том, что функция терпит разрыв в данной точке.
2) Существует ли предел ![]() ? То же самое, на нет – и непрерывности нет.
? То же самое, на нет – и непрерывности нет.
3) И завершающий тест, если до него, конечно, дело дошло: выполнено ли равенство ![]() ? Если да, то функция
? Если да, то функция ![]() непрерывна в точке
непрерывна в точке ![]() .
.
Но перед тем как опробовать эту простую схему, немного поговорим о видах разрыва поверхностей. Да их много, да их не особо принято классифицировать, но, ИМХО, это чрезвычайно полезно для качественного усвоения темы.
В первых же примерах статьи Предел функции двух переменных мы столкнулись с простейшим разрывом поверхности – разрывом в отдельно взятой точке. Вспоминаем функции ![]() , имеющие маленькую проблемку в начале координат, из-за которой мы делаем вывод о наличии разрывов в первом же пункте алгоритма. И уже здесь имеет место принципиальная разница в характере разрыва: в первом случае разрыв является неустранимым, поскольку в точке
, имеющие маленькую проблемку в начале координат, из-за которой мы делаем вывод о наличии разрывов в первом же пункте алгоритма. И уже здесь имеет место принципиальная разница в характере разрыва: в первом случае разрыв является неустранимым, поскольку в точке ![]() невозможно доопределить функцию ТАК, чтобы она стала непрерывной. Этот факт обусловлен несуществованием предела
невозможно доопределить функцию ТАК, чтобы она стала непрерывной. Этот факт обусловлен несуществованием предела ![]() – желающие могут открыть на соседней вкладке Пример № 1 предшествующего урока и вновь окинуть взглядом всю ситуацию.
– желающие могут открыть на соседней вкладке Пример № 1 предшествующего урока и вновь окинуть взглядом всю ситуацию.
Вторая же поверхность терпит разрыв устранимый, или как я его образно назвал, разрыв по типу «проколотое одеяло». Поскольку 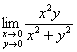 существует и равен нулю, то «подпредельную» функцию можно успешно доопределить до непрерывности в точке
существует и равен нулю, то «подпредельную» функцию можно успешно доопределить до непрерывности в точке ![]() («залепить отверстие жвачкой»). Это делается стандартно – кусочным образом:
(«залепить отверстие жвачкой»). Это делается стандартно – кусочным образом:
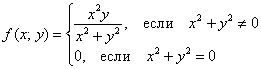
Проверим, что полученная функция непрерывна в точке ![]() :
:
1) функция определена в данной точке: ![]() ;
;
2) 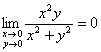 (см. Пример 2 урока Предел функции двух переменных);
(см. Пример 2 урока Предел функции двух переменных);
3) 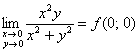 .
.
Что и требовалось проверить.
Но доопределить функцию, разумеется, можно и «плохо». Кстати, в этом примере обнаружение разрыва произойдёт только в 3-м пункте алгоритма.
Помимо точечных недоразумений, поверхности часто разрываются вдоль целых линий. Рассмотрим ещё одну простую функцию: ![]() . Так как
. Так как ![]() , то данная функция терпит разрыв во всех точках прямой
, то данная функция терпит разрыв во всех точках прямой ![]() . Для лучшего понимания ситуации повторим пройдённый материал: как изобразить на координатной плоскости
. Для лучшего понимания ситуации повторим пройдённый материал: как изобразить на координатной плоскости ![]() область определения рассматриваемой функции? Нужно начертить пунктиром прямую
область определения рассматриваемой функции? Нужно начертить пунктиром прямую ![]() .
.
Итак, функция ![]() терпит разрыв во всех точках прямой
терпит разрыв во всех точках прямой ![]() (на чертеже не обозначена), и соответствующая поверхность бесконечно близко приближается к «одноимённой» плоскости
(на чертеже не обозначена), и соответствующая поверхность бесконечно близко приближается к «одноимённой» плоскости ![]() :
:
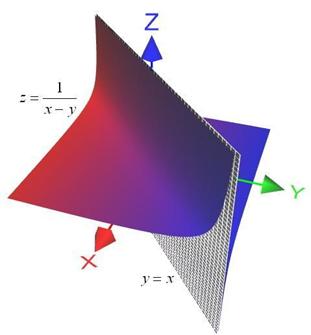
Иногда такую плоскость называют асимптотической плоскостью – по аналогии с асимптотами графика функции одной переменной.
Это был «чисто» бесконечный разрыв поверхности. Но, кроме такового, встречаются разрывы, где функцию всё же можно доопределить до непрерывности в некоторых, многих или даже во всех точках. Так, например, функция ![]() терпит разрыв по той же прямой
терпит разрыв по той же прямой ![]() , однако бесконечен он не везде. При любом допустимом маршруте к точке
, однако бесконечен он не везде. При любом допустимом маршруте к точке ![]() в плоскости
в плоскости ![]() поверхность «скручивается» к значению
поверхность «скручивается» к значению ![]() :
:
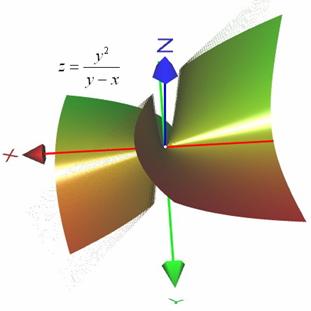
И действительно, легко убедиться, что 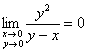 , следовательно, в начале координат разрыв можно устранить.
, следовательно, в начале координат разрыв можно устранить.
А сейчас наступил удачный момент для обещанного разбора интересной функции ![]() из Примера 8 урока Предел функции двух переменных. Данная функция представима в виде
из Примера 8 урока Предел функции двух переменных. Данная функция представима в виде ![]() и сократить на
и сократить на ![]() здесь можно лишь со следующей оговоркой:
здесь можно лишь со следующей оговоркой:
![]()
С геометрической точки зрения это означает, что из области определения функции «выпадает» прямая ![]() , и «одноимённая» плоскость
, и «одноимённая» плоскость ![]() , проходящая через ось
, проходящая через ось ![]() , «разрезает наше одеяло» (белая линия на чертеже):
, «разрезает наше одеяло» (белая линия на чертеже):
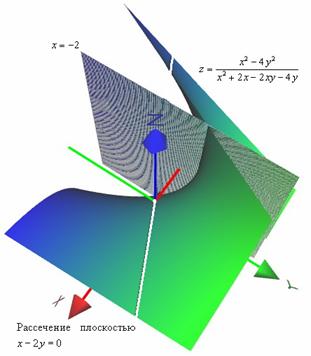
Функцию можно доопределить до непрерывности в любой точке разреза, за исключением значения ![]() , которое «наглухо убито» асимптотической плоскостью.
, которое «наглухо убито» асимптотической плоскостью.
Во избежание недосказанности следует отметить, что роль «асимптот» могут выполнять и другие поверхности, как правило, это различного рода цилиндры. Так, например, функция ![]() терпит разрыв по окружности
терпит разрыв по окружности ![]() и «одноимённый» круговой цилиндр как раз и играет такую роль:
и «одноимённый» круговой цилиндр как раз и играет такую роль:
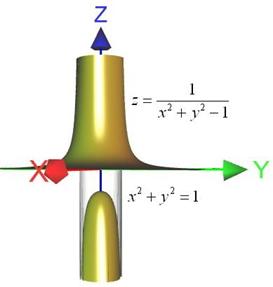
Здесь «чисто» бесконечный разрыв.
И в завершение нашего увлекательного обзора коротко о композиции: если некоторую функцию, возьмём ту же ![]() , «вложить» под всюду непрерывную функцию (косинус, синус, экспоненту и т. д.), то полученная сложная функция будет непрерывна/разрывна в тех же самых точках, что и «первоисточник» – так, функции
, «вложить» под всюду непрерывную функцию (косинус, синус, экспоненту и т. д.), то полученная сложная функция будет непрерывна/разрывна в тех же самых точках, что и «первоисточник» – так, функции 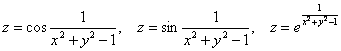 непрерывны везде, кроме точек окружности
непрерывны везде, кроме точек окружности ![]() .
.
…Никогда не думал, что о теореме непрерывности сложной функции можно рассказать одним предложением =)
Ну а теперь перейдём к практическим задачам:
Пример 1
Исследовать функцию ![]() на непрерывность в точке
на непрерывность в точке ![]()
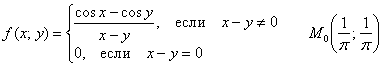
Решение проводится в три, а если повезёт, то и в меньшее количество шагов:
1) Координаты точки ![]() удовлетворяют условию
удовлетворяют условию ![]() , поэтому
, поэтому ![]() .
.
2) Проверим, существует ли общий предел в данной точке:
![]()
Используем тригонометрическую формулу ![]() и первый замечательный предел:
и первый замечательный предел:
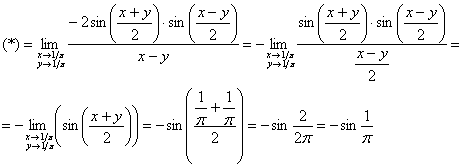
Да, общий предел существует, и на очереди завершающий пункт:
3) 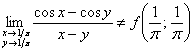 – предел функции в точке не равен значению данной функции в данной точке
– предел функции в точке не равен значению данной функции в данной точке
Ответ: функция терпит разрыв в точке ![]()
Этот разрыв является устранимым, и если функцию переопределить «правильным» образом: 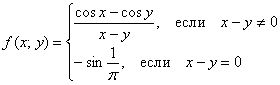 , то она станет непрерывной в точке
, то она станет непрерывной в точке ![]() .
.
Отрабатываем алгоритм:
Пример 2
Исследовать функцию ![]() на непрерывность в точке
на непрерывность в точке ![]()
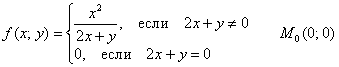
Краткое решение и ответ в конце урока.
Непрерывность функции также иногда называют непрерывностью по совокупному аргументу. Но кроме общей непрерывности, в теории и на практике рассматривается и частная непрерывность, а именно – непрерывность по переменной «икс» и непрерывность по переменной «игрек». Давайте разберёмся, что это такое и с чем это едят:
Пример 3
Исследовать функцию 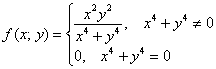 на непрерывность в точке
на непрерывность в точке ![]() :
:
а) по переменной ![]() ;
;
б) по переменной ![]() ;
;
в) по совокупному аргументу.
Решение: координаты точки ![]() (внимание!) НЕ удовлетворяют условию
(внимание!) НЕ удовлетворяют условию ![]() , поэтому:
, поэтому: ![]()
Функция определена в рассматриваемой точке, что включает зелёный свет к дальнейшему исследованию:
а) Как исследовать функцию ![]() на непрерывность в точке
на непрерывность в точке ![]() по переменной «икс»? Всё очень просто: в функцию нужно подставить конкретное значение
по переменной «икс»? Всё очень просто: в функцию нужно подставить конкретное значение ![]() и вычислить самый что ни на есть обычный предел функции одной переменной
и вычислить самый что ни на есть обычный предел функции одной переменной ![]() . Если окажется, что
. Если окажется, что ![]() , то функция непрерывна по
, то функция непрерывна по ![]() в данной точке.
в данной точке.
В нашем случае ![]() , таким образом:
, таким образом:
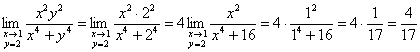 – неопределённости тут не было, и предел разрешился прямой подстановкой.
– неопределённости тут не было, и предел разрешился прямой подстановкой.
Внимание! Вычисленный предел не надо путать с повторным пределом. В повторном пределе значение «игрек» до поры до времени «заморожено» и не определено, здесь же мы сразу подставляем конкретное число ![]() . Геометрически это означает, что мы приближаемся к точке
. Геометрически это означает, что мы приближаемся к точке ![]() параллельно оси
параллельно оси ![]() (красные линии и стрелки на чертеже ниже).
(красные линии и стрелки на чертеже ниже).
По итогу: 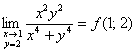 , значит, рассматриваемая функция непрерывна по «икс» в точке
, значит, рассматриваемая функция непрерывна по «икс» в точке ![]() .
.
б) Аналогично, чтобы исследовать функцию ![]() на непрерывность в точке
на непрерывность в точке ![]() по переменной «игрек», нужно взять конкретное значение
по переменной «игрек», нужно взять конкретное значение ![]() и вычислить предел
и вычислить предел ![]() . Если
. Если ![]() , то функция непрерывна по
, то функция непрерывна по ![]() в данной точке.
в данной точке.
Подставим в функцию ![]() и найдём ещё один предел от одной переменной, на этот раз – от переменной «игрек»:
и найдём ещё один предел от одной переменной, на этот раз – от переменной «игрек»:
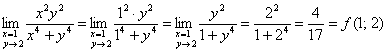 , значит, рассматриваемая функция непрерывна по «игрек» в точке
, значит, рассматриваемая функция непрерывна по «игрек» в точке ![]() .
.
Геометрически это означает, что мы приближаемся к точке ![]() параллельно оси
параллельно оси ![]() (синие линии и стрелки):
(синие линии и стрелки):
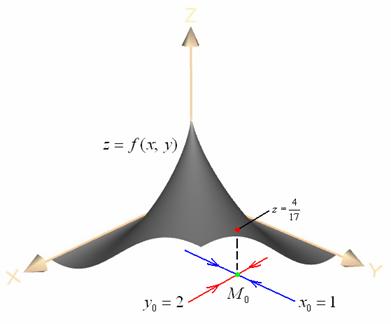
в) Уже из иллюстрации становится ясно, что функция непрерывна в точке ![]() и по совокупному аргументу, т. е. при произвольном к ней подходе. И в самом деле:
и по совокупному аргументу, т. е. при произвольном к ней подходе. И в самом деле:
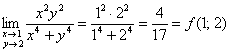
Ответ: а)-б)-в) непрерывна
Какова взаимосвязь частной и общей непрерывности? Если функция терпит разрыв по ![]() либо по
либо по ![]() в точке
в точке ![]() , то, понятно, что она является разрывной данной точке. НО из непрерывности функции по «икс» и по «игрек» ещё не следует её непрерывность по совокупному аргументу. Рассмотрим ту же функцию
, то, понятно, что она является разрывной данной точке. НО из непрерывности функции по «икс» и по «игрек» ещё не следует её непрерывность по совокупному аргументу. Рассмотрим ту же функцию 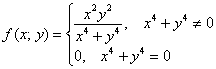 и точку
и точку ![]() . Функция определена в данной точке
. Функция определена в данной точке ![]() и при этом непрерывна, как по «икс», так и по «игрек»:
и при этом непрерывна, как по «икс», так и по «игрек»:
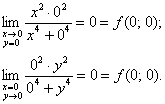
Однако общего предела 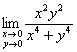 не существует (проверьте самостоятельно), а значит, и о непрерывности по совокупному аргументу речи не идёт.
не существует (проверьте самостоятельно), а значит, и о непрерывности по совокупному аргументу речи не идёт.
Геометрически ситуация очень проста: непрерывность по «икс» (красный цвет) и по «игрек» (синий цвет) реализуется по частным маршрутам к точке ![]() (зелёная точка), к которой мы продвигаемся прямо по координатным осям. При этом соответствующие значения функции даже не приближаются, а непосредственно равны нулю (т. к. график проходит через оси
(зелёная точка), к которой мы продвигаемся прямо по координатным осям. При этом соответствующие значения функции даже не приближаются, а непосредственно равны нулю (т. к. график проходит через оси ![]() ):
):
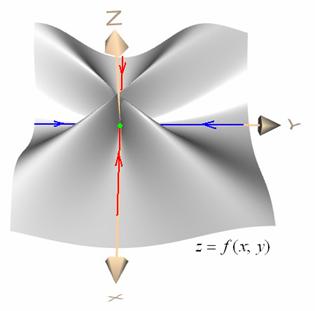
Но при любом другом подходе к началу координат, поверхность будет приближаться к оси ![]() на различных ненулевых высотах. Разрыв здесь неустраним, и, кстати, его природа точь-в-точь такая же, как и в Примере № 1 статьи Предел функции двух переменных.
на различных ненулевых высотах. Разрыв здесь неустраним, и, кстати, его природа точь-в-точь такая же, как и в Примере № 1 статьи Предел функции двух переменных.
Следующие два примера для самостоятельного решения. Как повелось, попроще:
Пример 4
Исследовать функцию 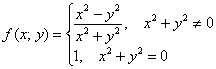 на непрерывность в точке
на непрерывность в точке ![]() :
:
а) по переменной ![]() ;
;
б) по переменной ![]() ;
;
в) по совокупному аргументу.
И посложнее:
Пример 5
Те же задания для функции 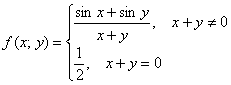 и точки
и точки ![]() .
.
Решения и ответы совсем близко.
На протяжении всего урока речь преимущественно шла о непрерывности функции в отдельно взятой точке, и возникает вопрос, а как сформулировать это понятие для целой области (множества точек плоскости ![]() )? Данный подход уже неоднократно встречался в курсе высшей математики, он прост и гениален: функция
)? Данный подход уже неоднократно встречался в курсе высшей математики, он прост и гениален: функция ![]() непрерывна в некоторой области, если она непрерывна в каждой точке данной области.
непрерывна в некоторой области, если она непрерывна в каждой точке данной области.
Понятие непрерывности распространяется и на функции бОльшего количества переменных, и если вам нужна соответствующая информация, пожалуйста, обратитесь к учебной литературе – теоретические и практические выкладки будут родственны, но геометрический смысл, естественно, пропадёт.
На этом основные моменты темы раскрыты, и прямо по курсу дифференциальное исчисление функций нескольких переменных.
Семь футов под килем!
Решения и ответы:
Пример 2. Решение:
1) ![]() – функция определена в данной точке.
– функция определена в данной точке.
2) Вычислим предел по прямой ![]() :
:
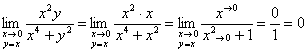
Вычислим предел по параболе ![]() :
:

Значение предела зависит от пути интегрирования, значит, общего предела не существует.
Вывод: функция терпит неустранимый разрыв в точке ![]() .
.
Примечание: переход к полярным координатам может привести к ошибочному выводу: 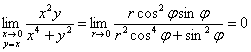 – при любом значении «фи», но, тем не менее, двойного предела не существует! Ибо этого условия не достаточно.
– при любом значении «фи», но, тем не менее, двойного предела не существует! Ибо этого условия не достаточно.
Пример 4. Решение: координаты точки ![]() удовлетворяют условию
удовлетворяют условию ![]() , поэтому:
, поэтому:
![]() – функция определена в данной точке.
– функция определена в данной точке.
а) Исследуем функцию на непрерывность по ![]() :
:
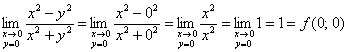 , значит, рассматриваемая функция непрерывна по
, значит, рассматриваемая функция непрерывна по ![]() в данной точке.
в данной точке.
б) Исследуем функцию на непрерывность по ![]() :
:
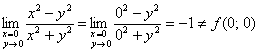 , значит, рассматриваемая функция не является непрерывной по
, значит, рассматриваемая функция не является непрерывной по ![]() в данной точке.
в данной точке.
в) Из предыдущего пункта следует, что функция не является непрерывной по совокупному аргументу.
Примечание: здесь также можно показать, что предела 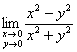 не существует (см. Пример № 3 урока Предел функции двух переменных).
не существует (см. Пример № 3 урока Предел функции двух переменных).
Ответ: а) непрерывна, б)-в) не является непрерывной
Пример 5. Решение: координаты точки ![]() удовлетворяют условию
удовлетворяют условию ![]() , поэтому
, поэтому ![]() – функция определена в данной точке.
– функция определена в данной точке.
а) Непрерывность по ![]() .
.
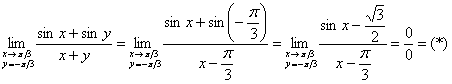
Проведём замену: ![]()
Если ![]() , то
, то ![]()
Далее используем тригонометрическую формулу ![]() и первый замечательный предел:
и первый замечательный предел:
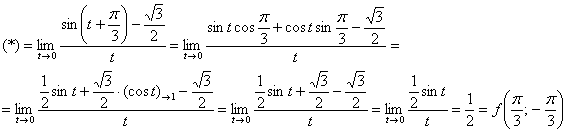
Таким образом, функция непрерывна по ![]() в данной точке.
в данной точке.
б) Непрерывность по ![]() .
.
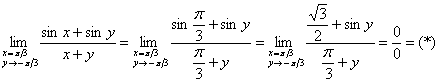
Проведём замену: ![]()
Если ![]() , то
, то ![]()
Используем тригонометрическую формулу ![]() и первый замечательный предел:
и первый замечательный предел:
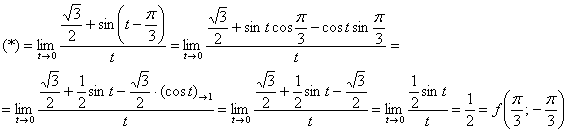
Таким образом, функция непрерывна по ![]() в данной точке.
в данной точке.
в) Непрерывность по совокупному аргументу.
![]()
Используем формулу ![]() и первый замечательный предел
и первый замечательный предел ![]() , где
, где ![]() :
:
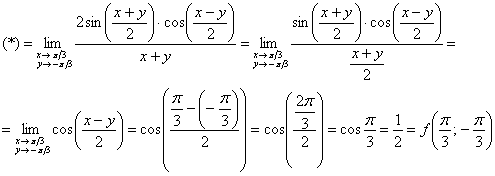
Таким образом, функция непрерывна и по совокупному аргументу в данной точке.
Ответ: а)-б)-в) непрерывна
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright