УравнениЯ прямой в пространстве

Здравствуйте-здравствуйте! Впервые или снова, но очень рад вас видеть! Продолжаем знакомиться с пространственной геометрией – миром, в котором мы живём. На первом уроке мы вдоль и поперёк рассмотрели уравнение плоскости, а сейчас очередь дошла до моей очередной жертвы – прямой в пространстве.

Сначала разберём вопросы, связанные с уравнениЯМИ прямой в пространстве, посмотрим, как может располагаться прямая относительно координатных плоскостей, координатных осей и затем научимся решать типовые задачи. Я добросовестно постараюсь рассказать всё самое главное, что связано с пространственными прямыми.

Для лёгкого понимания темы рекомендую проштудировать уравнение «плоской» прямой, поскольку будет очень много похожих вещей. Но будут и отличия, на одно из которых вы уже наверняка обратили внимание. Я выделял большими буквами окончание слова «уравнение», подчеркивая, что оно находится ВО МНОЖЕСТВЕННОМ ЧИСЛЕ. И это не случайно, своеобразие пространственной прямой состоит в том, что она задаётся не одним уравнением, а некоторым множеством уравнений. Высшая математика не озадачивает нас улыбкой Джоконды, поэтому надвинем на лоб строгую параллельность морщин и приступим к делу. Если вас интересует что-то конкретное, используйте быстрые ссылки:

канонические уравнения прямой (по точке и направляющему вектору);
уравнения прямой по двум точкам;
параметрические уравнения прямой;
прямая, заданная пересечением двух плоскостей.

Типовые задачи с пространственной прямой

Как составить уравнения прямой в пространстве?

Аналогично «плоской» прямой, существует несколько способов, которыми мы можем задать прямую в пространстве. Начнём с канонов – точки и направляющего вектора прямой:

Канонические уравнения прямой

Если известна некоторая точка пространства , принадлежащая прямой, и направляющий вектор данной прямой, то канонические уравнения этой прямой выражаются формулами:

Приведённая запись предполагает, что координаты направляющего вектора не равны нулю. Что делать, если одна или две координаты нулевые, мы рассмотрим чуть позже.

Как и в статье Уравнение плоскости, для простоты будем считать, что во всех задачах урока действия проводятся в ортонормированном базисе пространства.

Пример 1

Составить канонические уравнения прямой по точке и направляющему вектору

Решение: канонические уравнения прямой составим по формуле:

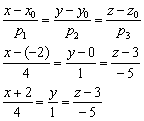
Ответ:

Что следует отметить в этом очень простом примере? Во-первых, полученные уравнения НЕ НАДО сокращать на единицу: . Сократить, точнее, можно, но это непривычно режет глаз и создаёт неудобства в ходе решения задач.

А во-вторых, это проверка.Сначала смотрим на знаменатели уравнений и сверяемся – правильно ли там записаны координаты направляющего вектора . Нет, не подумайте, у нас не урок в детском садике «Тормозок». Данный совет очень важен, поскольку позволяет полностью исключить ошибку по невнимательности. Никто не застрахован, а вдруг неправильно переписали? Наградят премией Дарвина по геометрии.

Далее подставляем координаты точки в найденные уравнения:

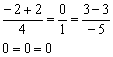
Получены верные равенства, значит, координаты точки удовлетворяют нашим уравнениям, и сама точка действительно принадлежит данной прямой.

Проверка очень легко (и быстро!) выполняется устно.

В ряде задач требуется найти какую-нибудь другую точку , принадлежащую данной прямой. Как это сделать?

Берём полученные уравнения и мысленно «отщипываем», например, левый кусочек: . Теперь этот кусочек приравниваем к любому числу (помним, что ноль уже был), например, к единице: . Так как , то и два других «куска» тоже должны быть равны единице. По сути, нужно решить систему:

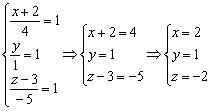
Проверим, удовлетворяет ли найденная точка уравнениям :

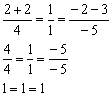
Получены верные равенства, значит, точка действительно лежит на данной прямой.

Выполним чертёж в прямоугольной системе координат. Заодно вспомним, как правильно откладывать точки в пространстве:
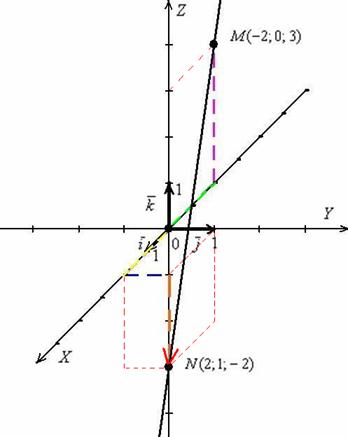
Прямая в пространстве

Строим точку :
– от начала координат в отрицательном направлении оси откладываем отрезок первой координаты (зелёный пунктир);
– вторая координата нулевая, поэтому «не дёргаемся» с оси ни влево, ни вправо;
– в соответствие с третьей координатой отмеряем три единицы вверх (фиолетовый пунктир).

Строим точку : отмеряем две единицы «на себя» (желтый пунктир), одну единицу вправо (синий пунктир) и две единицы вниз (коричневый пунктир). Коричневый пунктир и сама точка наложились на координатную ось, обратите внимание, что они находятся в нижнем полупространстве и ПЕРЕД осью .

Сама прямая проходит над осью и, если меня не подводит глазомер, над осью . Не подводит, убедился аналитически. Если бы прямая проходила ЗА осью , то следовало бы стереть ластиком частичку линии сверху и снизу точки скрещивания.

У прямой бесконечно много направляющих векторов, например:
(красная стрелка)

Получился в точности исходный вектор , но это чистая случайность, такую уж я выбрал точку . Все направляющие векторы прямой коллинеарны, и их соответствующие координаты пропорциональны (более подробно – см. Линейная (не) зависимость векторов. Базис векторов). Так, векторы тоже будут направляющими векторами данной прямой.

Дополнительную информацию о построении трёхмерных чертежей на клетчатой бумаге можно найти в начале методички Графики и свойства функций. В тетради разноцветные пунктирные дорожки к точкам (см. чертёж) обычно тонко прочерчивают простым карандашом тем же пунктиром.

Разберёмся с частными случаями, когда одна или две координаты направляющего вектора нулевые. Попутно продолжаем тренировку пространственного зрения, которая началась в начале урока Уравнение плоскости. И вновь я расскажу вам сказку о голом короле – нарисую пустую систему координат и буду убеждать вас, что там есть пространственные прямые =)
Расположение прямой относительно координатных осей и координатных плоскостей

Проще перечислить все шесть случаев:

1) Для точки и направляющего вектора канонические уравнения прямой распадаются на три отдельных уравнения: .

Или короче:

Пример 2: составим уравнения прямой по точке и направляющему вектору :

Что это за прямая? Направляющий вектор прямой коллинеарен орту , значит, данная прямая будет параллельна оси . Канонические уравнения следует понимать так:
а) – «игрек» и «зет» постоянны, равны конкретным числам;
б) переменная «икс» может принимать любые значения: (на практике данное уравнение, как правило, не записывают).

В частности, уравнения задают саму ось . Действительно, «икс» принимает любое значение, а «игрек» и «зет» всегда равны нулю.

Рассматриваемые уравнения можно интерпретировать и другим образом: посмотрим, например, на аналитическую запись оси абсцисс: . Ведь это уравнения двух плоскостей! Уравнение задаёт координатную плоскость , а уравнение – координатную плоскость . Правильно думаете – данные координатные плоскости пересекаются по оси . Способ, когда прямая в пространстве задаётся пересечением двух плоскостей, мы рассмотрим в самом конце урока.

Два похожих случая:

2) Канонические уравнения прямой, проходящей через точку параллельно вектору , выражаются формулами .

Такие прямые будут параллельны координатной оси . В частности, уравнения задают координатную саму ось ординат.

3) Канонические уравнения прямой, проходящей через точку параллельно вектору , выражаются формулами .

Данные прямые параллельны координатной оси , а уравнения задают саму ось аппликат.

Обкатываем вторую тройку:

4) Для точки и направляющего вектора канонические уравнения прямой распадаются на пропорцию и уравнение плоскости .

Пример 3: составим уравнения прямой по точке и направляющему вектору :

Разберём суть полученной записи. Уравнение задаёт плоскость в пространстве, причём данная плоскость параллельна «родной» координатной плоскости . Пропорция же – есть уравнение «плоской» прямой, единственное, эта прямая находится не на плоскости , а на высоте .

Если высота нулевая: , то уравнения принимают вид , и вот это уже в точности наша «плоская» прямая, лежащая в плоскости .

Таким образом, рассмотренный случай задаёт прямую, параллельную координатной плоскости . Действительно, задумайтесь, ведь направляющий вектор параллелен данной плоскости, ведь «зетовая» координата равна нулю.

Аналогично:

5) Прямая, заданная точкой и направляющим вектором , параллельна координатной плоскости , и её канонические уравнения выражаются формулами: .

В частности, уравнения определяют прямую, лежащую в плоскости .

6) Прямая, заданная точкой и направляющим вектором , параллельна координатной плоскости , и её канонические уравнения выражаются формулами: .

В частности, уравнения определяют прямую, лежащую в плоскости .

Настала пора хорошо закусить:

Пример 4

Записать канонические уравнения прямой, если известна точка и направляющий вектор данной прямой.

а)
б)
в) Записать уравнения прямой, проходящей через точку параллельно оси .

Это примеры для самостоятельного решения, ответы в конце урока.

Постарайтесь не пренебрегать примерами данного урока! Задачи вроде бы элементарны, но если на них забить, то в дальнейшем появятся серьёзные затруднения. Причём, в простых вещах.

Как составить уравнения пространственной прямой по двум точкам?

Если известны две точки пространства , то уравнения прямой, проходящей через данные точки, выражаются формулами:

Унылый частный случай предыдущего параграфа. И в самом деле, вектор является направляющим вектором прямой.

По возможности, рекомендую не пользоваться данными формулами, по причине вероятных «накладок» оформления – в случаях, когда внизу получаются нули. Оптимален следующий алгоритм:

Пример 5

Составить уравнения прямой, проходящей через точки .

Решение: найдём направляющий вектор прямой:

Уравнения прямой составим по точке (можно было выбрать точку ) и направляющему вектору :

Ответ:

В принципе, можно было сократить знаменатели пропорции на 2 и записать ответ в виде , но в данном случае надобности в этом нет никакой.

Выполним проверку. Подставим координаты точки в полученные уравнения:

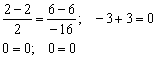
Получены верные равенства.

Подставим координаты точки :

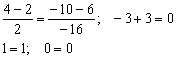
Получены верные равенства.

Вывод: канонические уравнения прямой составлены правильно.

Пример 6

Составить уравнения прямой, проходящей через точки

Это пример для самостоятельного решения. Решение и ответ в конце урока.

Параметрические уравнения прямой в пространстве

Обязательно прочитайте данный параграф! Параметрические уравнения, конечно, не альфа и омега пространственной геометрии, но рабочий муравей многих задач. Причём, этот вид уравнений часто применяется неожиданно, и я бы сказал, изящно.

Если известна точка , принадлежащая прямой, и направляющий вектор данной прямой, то параметрические уравнения этой прямой задаются системой:

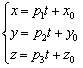
Параметрические уравнения прямой в пространстве

О самом понятии параметрических уравнений я рассказывал на уроках Уравнение прямой на плоскости и Производная параметрически заданной функции.

Всё проще пареной репы, поэтому придётся приперчить задачу:

Пример 7

Составить параметрические уравнения следующих прямых:

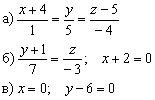
Решение: прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.

а) Из уравнений снимаем точку и направляющий вектор: . Точку можно выбрать и другую (как это сделать – рассказано выше), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.

Составим параметрические уравнения данной прямой:

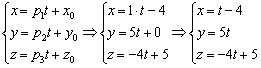
Удобство параметрических уравнений состоит в том, что с их помощью очень легко находить другие точки прямой. Например, найдём точку , координаты которой, скажем, соответствуют значению параметра :

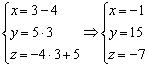
Таким образом:

б) Рассмотрим канонические уравнения . Выбор точки здесь несложен, но коварен: (будьте внимательны, не перепутайте координаты!!!). Как вытащить направляющий вектор? Можно порассуждать, чему параллельна данная прямая, а можно использовать простой формальный приём: в пропорции находятся «игрек» и «зет», поэтому запишем направляющий вектор , а на оставшееся место поставим ноль: .

Составим параметрические уравнения прямой:

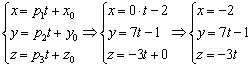
в) Перепишем уравнения в виде , то есть «зет» может быть любым. А если любым, то пусть, например, . Таким образом, точка принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях находятся «икс» и «игрек», и в направляющем векторе на данных местах записываем нули: . На оставшееся место ставим единицу: . Вместо единицы подойдёт любое число, кроме нуля.

Запишем параметрические уравнения прямой:

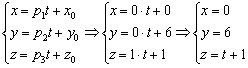
Для тренировки:

Пример 8

Составить параметрические уравнения следующих прямых:

Решения и ответы в конце урока. Полученные вами ответы могут несколько отличаться от моих ответов, дело в том, что параметрические уравнения можно записать не единственным способом. Важно, чтобы ваши и мои направляющие векторы были коллинеарны, и ваша точка «подходила» к моим уравнениям (ну, или наоборот, моя точка к вашим уравнениям).

Как ещё можно задать прямую в пространстве? Хочется что-нибудь придумать с вектором нормали. Однако номер не пройдёт, у пространственной прямой нормальные векторы могут смотреть совершенно в разные стороны.

Ещё об одном способе уже упоминалось на уроке Уравнение плоскости и в начале этой статьи.

Прямая, заданная пересечением двух плоскостей

Если плоскости пересекаются,
то система линейных уравнений задаёт прямую в пространстве.

То есть прямая задана уравнениями двух плоскостей. Типовая и распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:

Пример 9

Записать канонические уравнения прямой

Решение: чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….

1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? В системе уравнений нужно обнулить какую-нибудь координату. Пусть , тогда получаем систему двух линейных уравнений с двумя неизвестными: . Почленно складываем уравнения и находим решение системы:

Таким образом, точка принадлежит данной прямой. Обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки можно проводить мысленно или на черновике.

Выполним проверку, подставим координаты точки в исходную систему уравнений: . Получены верные равенства, значит, действительно .

2) Как найти направляющий вектор прямой? Его нахождение наглядно демонстрирует следующий схематический чертёж:
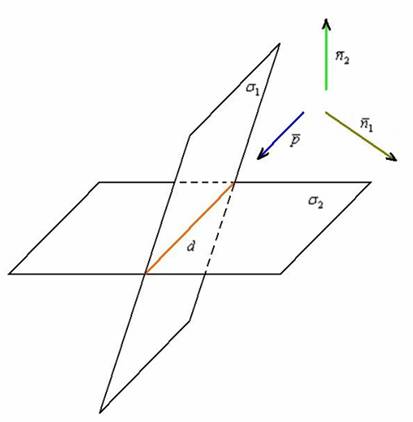
Нахождение вектора нормали, когда прямая задана пересечением двух плоскостей
Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей. А если , то вектор «пэ» найдём как векторное произведение векторов нормали: .

Из уравнений плоскостей снимаем их векторы нормали:

И находим направляющий вектор прямой:

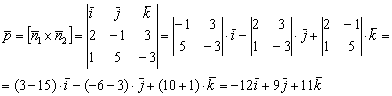
Как проверить результат, рассматривалось в статье Векторное произведение векторов.

3) Составим канонические уравнения прямой по точке и направляющему вектору :

Ответ:

На практике можно пользоваться готовой формулой: если прямая задана пересечением двух плоскостей , то вектор является направляющим вектором данной прямой.

Пример 10

Записать канонические уравнения прямой

Это пример для самостоятельного решения. Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения и подставьте в моё уравнение (или наоборот).

Полное решение и ответ в конце урока.

Во второй части урока мы рассмотрим взаимное расположение прямых в пространстве, а также разберём задачи, которые связаны с пространственными прямыми и точками. Терзают меня смутные ожидания, что материала будет прилично, поэтому лучше всё-таки сделать отдельную веб страницу.

Добро пожаловать: задачи с прямой в пространстве >>>

Решения и ответы:

Пример 4. Ответы:

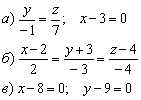
Пример 6. Решение: найдём направляющий вектор прямой:

Уравнения прямой составим по точке и направляющему вектору :

Ответ: («игрек» – любое)

Пример 8. Решения и ответы:

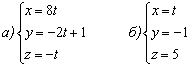
в) Найдём направляющий вектор прямой: . Параметрические уравнения прямой составим по точке (можно выбрать точку «бэ») и направляющему вектору :

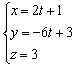
Пример 10. Решение: найдём какую-нибудь точку, принадлежащую данной прямой. Пусть , тогда: . Точка . Найдём направляющий вектор прямой, используем формулу:

Составим канонические уравнения прямой по точке и направляющему вектору :

Ответ:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?