


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Числовые ряды повышенной сложности
Не ходите, дети, в Африку гулять
Битый час мучаетесь со сходимостью числового ряда? Упорно не работают признаки сравнения, признаки Даламбера и Коши? Сто долларов в зачётку. В такой ситуации неоднократно оказывается практически каждый студент… сложная производная, сложный интеграл, сложная задача по геометрии и вот теперь очередь дошла до неприступного числового ряда. Причём, злись не злись, психуй не психуй, а покорить его надо.
Насколько часто такие ряды попадаются на практике? По моей субъективной оценке, их объём составляет где-то 10-15% от общего количества задач типовой работы по теме (если у вас заметно больше – Ряды для чайников). Таким образом, вероятность приятной встречи очень велика, и данная статья как раз рассчитана на тех читателей, которые уже достаточно уверенно умеют исследовать сходимость числового ряда ![]() стандартными методами, но зашли в тупик с очередным примером.
стандартными методами, но зашли в тупик с очередным примером.
В чём состоит трудность и где может быть загвоздка? Отложим в сторону намыленную верёвку, спокойно проанализируем причины и ознакомимся с практическими приёмами решения.
Первое, и самое главное: в подавляющем большинстве случаев для исследования сходимости ряда нужно применить какой-нибудь знакомый способ, но общий член ряда ![]() набит настолько хитрой начинкой, что совершенно не очевидно, что с ней делать. И вы ходите по кругу: не срабатывает первый признак, не годится второй, не получается третьим, четвёртым, пятым методом, потом черновики отбрасываются в сторону и всё начинается заново. Обычно это связано с недостатком опыта или пробелами в других разделах математического анализа. В частности, если запущены пределы последовательностей и поверхностно разобраны пределы функций, то придётся туго.
набит настолько хитрой начинкой, что совершенно не очевидно, что с ней делать. И вы ходите по кругу: не срабатывает первый признак, не годится второй, не получается третьим, четвёртым, пятым методом, потом черновики отбрасываются в сторону и всё начинается заново. Обычно это связано с недостатком опыта или пробелами в других разделах математического анализа. В частности, если запущены пределы последовательностей и поверхностно разобраны пределы функций, то придётся туго.
Иными словами, человек просто не видит нужный приём решения в силу недостатка знаний или опыта.
Бывает виновато и «затмение», когда, например, элементарно не выполнен необходимый признак сходимости ряда, но по незнанию, невнимательности либо небрежности это выпадает из поля зрения. И получается как в той байке, где профессор математики решил детскую задачку с помощью диких рекуррентных последовательностей и числовых рядов =)
В лучших традициях сразу живые примеры: ряды ![]() и их родственники – расходятся, так как в теории доказаны пределы последовательностей
и их родственники – расходятся, так как в теории доказаны пределы последовательностей ![]() . Скорее всего, в первом семестре из вас вытрясут душу за доказательство на 1-2-3 страницы, но сейчас вполне достаточно показать невыполнение необходимого условия сходимости ряда, сославшись на известные факты. Известные? Если студент не знает, что корень энной степени – штука чрезвычайно мощная, то, скажем, ряды
. Скорее всего, в первом семестре из вас вытрясут душу за доказательство на 1-2-3 страницы, но сейчас вполне достаточно показать невыполнение необходимого условия сходимости ряда, сославшись на известные факты. Известные? Если студент не знает, что корень энной степени – штука чрезвычайно мощная, то, скажем, ряды ![]() поставят его в тупик. Хотя решение, как дважды два:
поставят его в тупик. Хотя решение, как дважды два: ![]() , т. е. по понятной причине оба ряда расходятся. Скромного комментария «данные пределы доказаны в теории» (или даже вовсе его отсутствия) вполне хватит для зачёта, всё-таки выкладки достаточно тяжёлые и относятся они точно не к разделу числовых рядов.
, т. е. по понятной причине оба ряда расходятся. Скромного комментария «данные пределы доказаны в теории» (или даже вовсе его отсутствия) вполне хватит для зачёта, всё-таки выкладки достаточно тяжёлые и относятся они точно не к разделу числовых рядов.
А изучив ближайшие примеры, вы будете только удивляться краткости и прозрачности многих решений:
Пример 1
Исследовать сходимость ряда
![]()
Решение: прежде всего, проверяем выполнение необходимого признака сходимости. Это не формальность, а отличный шанс расправиться с примером «малой кровью».
Числовая последовательность ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() , поэтому
, поэтому ![]() , то есть необходимый признак сходимости выполнен, и ряд может, как сходиться, так и расходиться. Ну что же, попытка – не пытка. Следует отметить, что для чайников тот же предел
, то есть необходимый признак сходимости выполнен, и ряд может, как сходиться, так и расходиться. Ну что же, попытка – не пытка. Следует отметить, что для чайников тот же предел ![]() вовсе не очевиден, поэтому по ходу дела я ненавязчиво расставляю ссылки ;-)
вовсе не очевиден, поэтому по ходу дела я ненавязчиво расставляю ссылки ;-)
Таким образом, нужно использовать какой-либо признак. Но какой? Предельный признак сравнения явно не подходит, поскольку в общий член ряда затесался логарифм, признаки Даламбера и Коши тоже не приводят к результату. Если бы у нас был ![]() , то худо-бедно можно было бы вывернуться через интегральный признак.
, то худо-бедно можно было бы вывернуться через интегральный признак.
«Осмотр места происшествия» наводит на мысль о расходящемся ряде ![]() (случай обобщенного гармонического ряда), но опять же возникает вопрос, как учесть логарифм в числителе?
(случай обобщенного гармонического ряда), но опять же возникает вопрос, как учесть логарифм в числителе?
Остаётся самый первый признак сравнения, основанный на неравенствах, который часто не принимается во внимание и пылится на дальней полке. Распишем ряд подробнее:
![]()
Напоминаю, что ![]() – неограниченно растущая числовая последовательность:
– неограниченно растущая числовая последовательность:
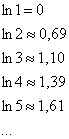
И, начиная с номера ![]() , будет выполнено неравенство
, будет выполнено неравенство ![]() :
:
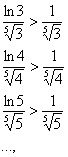
то есть члены ряда ![]() будут ещё больше соответствующих членов расходящегося ряда
будут ещё больше соответствующих членов расходящегося ряда ![]() .
.
В итоге, ряду ![]() ничего не остаётся, как тоже расходиться.
ничего не остаётся, как тоже расходиться.
Здесь я невзначай использовал простое утверждение математического анализа: сходимость или расходимость числового ряда зависит от его «бесконечного хвоста» (остатка). В нашем случае мы можем не принимать во внимание тот факт, что неравенство ![]() неверно для первых двух номеров – это не оказывает влияния на сделанный вывод.
неверно для первых двух номеров – это не оказывает влияния на сделанный вывод.
Чистовое оформление примера должно выглядеть примерно так:
“
Сравним данный ряд с расходящимся рядом ![]() .
.
Для всех номеров, начиная с ![]() , выполнено неравенство
, выполнено неравенство ![]() , следовательно, по признаку сравнения исследуемый ряд расходится.
, следовательно, по признаку сравнения исследуемый ряд расходится.
“
Три строчки. Всё!
Естественно, такому лаконичному оформлению предшествует мысленный анализ либо разбор полётов на черновике. Само собой не возбраняется расписать решение и подробно, но почти всегда идёт «на ура» и короткая версия.
Пример 2
Исследовать сходимость ряда
![]()
Это пример для самостоятельного решения. Подумайте, подберите ряд для сравнения, распишите ряды. Вот вам и истинный математический анализ =) Примерный образец оформления в конце урока.
С увлечением рассматриваем в бинокль других дикобразов:
Пример 3
Исследовать сходимость ряда
![]()
Решение: константа-множитель общего члена не влияет на сходимость или расходимость ряда, поэтому выносим её за пределы суммы:
![]()
Напрашивается сравнение с рядом ![]() , и предчувствие не обманывает. Всего-то лишь немного проанализировать чудо в
, и предчувствие не обманывает. Всего-то лишь немного проанализировать чудо в перьях синусах:
Последовательность ![]() – ограничена:
– ограничена:
![]()
Следовательно, для любых натуральных номеров справедливо следующее неравенство:
![]()
А дробь с бОльшим знаменателем будет меньше дроби с мЕньшим знаменателем:
![]() – для всех «эн» (кто не врубился во фразу – условный пример:
– для всех «эн» (кто не врубился во фразу – условный пример: ![]() ).
).
То есть члены ряда ![]() ещё меньше соответствующих членов сходящегося ряда
ещё меньше соответствующих членов сходящегося ряда ![]() , и нашему ряду тоже ничего не остаётся, как сходиться.
, и нашему ряду тоже ничего не остаётся, как сходиться.
Вывод: по признаку сравнения исследуемый ряд сходится.
Если что-то показалось мутным или не очень понятным, рекомендую расписать члены обоих рядов (на худой конец приблизительно вычислить их на калькуляторе), сравнить между собой и снова перечитать выкладки.
Второй способ решения: в данном примере годится и предельный признак сравнения. Сравним исследуемый ряд со сходящимся рядом ![]() :
:
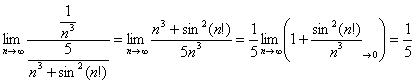
Обратите внимание, что с выносом «пятёрки» тут можно не возиться и отношение общих членов выгоднее составить именно так, а не наоборот: 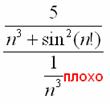 . На завершающем этапе использована теорема: произведение бесконечно малой последовательности на ограниченную последовательность – есть бесконечно малая последовательность (см. урок о числовых последовательностях). В нашем случае последовательность
. На завершающем этапе использована теорема: произведение бесконечно малой последовательности на ограниченную последовательность – есть бесконечно малая последовательность (см. урок о числовых последовательностях). В нашем случае последовательность ![]() – бесконечно малА, а
– бесконечно малА, а ![]() – ограничена, следовательно,
– ограничена, следовательно, ![]() .
.
Вывод: в пределе получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом ![]() .
.
Но предельный признак сравнения работает далеко не всегда. Пара коротких заданий для самостоятельного решения:
Пример 4
Исследовать сходимость ряда
![]()
Многие читатели уже видят, с чем нужно сравнивать, и что ряд явно расходится. Здесь не пригоден признак сравнения с неравенствами, поскольку ![]() принимает как положительные, так и отрицательные значения, а значит, условие
принимает как положительные, так и отрицательные значения, а значит, условие ![]() справедливо далеко не всегда.
справедливо далеко не всегда.
Пример 5
Исследовать сходимость ряда
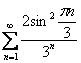
Здесь же ситуация обратная – не работает предельный признак сравнения.
Примерные образцы оформления задач в конце урока.
Не редкость, когда приходится проводить двухходовое (а то и трёхходовое) рассуждение:
Пример 6
Исследовать сходимость ряда
![]()
Решение: сначала аккуратно разбираемся с тарабарщиной числителя. Последовательность ![]() – ограничена:
– ограничена: ![]() . Тогда:
. Тогда:
![]()
Сравним наш ряд с рядом ![]() . В силу только что полученного двойного неравенства, для всех «эн» будет выполнено:
. В силу только что полученного двойного неравенства, для всех «эн» будет выполнено:
![]()
Теперь сравним ряд ![]() с расходящимся гармоническим рядом
с расходящимся гармоническим рядом ![]() .
.
Знаменатель дроби ![]() меньше знаменателя дроби
меньше знаменателя дроби ![]()
![]() , поэтому сама дробь
, поэтому сама дробь ![]() – больше дроби
– больше дроби ![]() (распишите несколько первых членов, если не понятно). Таким образом, для любого «эн»:
(распишите несколько первых членов, если не понятно). Таким образом, для любого «эн»:
![]()
А значит, по признаку сравнения ряд ![]() расходится вместе с гармоническим рядом.
расходится вместе с гармоническим рядом.
Если немного видоизменить знаменатель: ![]() , то первая часть рассуждений будет аналогична:
, то первая часть рассуждений будет аналогична: ![]() . Но вот для доказательства расходимости ряда
. Но вот для доказательства расходимости ряда ![]() уже применИм только предельный признак сравнения, так как неравенство
уже применИм только предельный признак сравнения, так как неравенство ![]() неверно.
неверно.
Ситуация со сходящимися рядами «зеркальна», то есть, например, для ряда ![]() можно использовать оба признака сравнения (неравенство
можно использовать оба признака сравнения (неравенство ![]() справедливо), а для ряда
справедливо), а для ряда ![]() – только предельный признак (неравенство
– только предельный признак (неравенство ![]() неверно).
неверно).
Продолжаем наше сафари по дикой природе, где на горизонте замаячило стадо грациозных и сочных антилоп:
Пример 7
Исследовать сходимость ряда
![]()
Решение: необходимый признак сходимости выполняется, и мы снова задаёмся классическим вопросом: что делать? Перед нами нечто напоминающее сходящийся ряд ![]() , однако, чёткого правила тут нет – такие ассоциации зачастую обманчивы.
, однако, чёткого правила тут нет – такие ассоциации зачастую обманчивы.
Зачастую, да не в этот раз. С помощью предельного признака сравнения сравним наш ряд со сходящимся рядом ![]() . В ходе вычисления предела используем замечательный предел
. В ходе вычисления предела используем замечательный предел ![]() , где в качестве бесконечно малой величины выступает
, где в качестве бесконечно малой величины выступает ![]() (да, замечательные пределы работают не только в точке ноль, но и в других точках, а также на бесконечности):
(да, замечательные пределы работают не только в точке ноль, но и в других точках, а также на бесконечности):
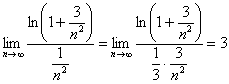
Получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом ![]() .
.
Вместо применения стандартного искусственного приёма домножения и деления на «тройку», можно было изначально провести сравнение со сходящимся рядом ![]() .
.
Но здесь желательна оговорка, что константа-множитель общего члена не влияет на сходимость ряда. И как раз в таком стиле оформлено решение следующего примера:
Пример 8
Исследовать сходимость ряда
![]()
Образец в конце урока.
Где замечательные пределы, там неподалёку и замечательные эквивалентности:
Пример 9
Исследовать сходимость ряда
![]()
Решение: в предыдущих примерах мы пользовались ограниченностью синуса, но сейчас это свойство оказывается вне игры. Знаменатель дроби более высокого порядка роста, чем числитель, поэтому при ![]() аргумент синуса и весь общий член бесконечно малЫ. Необходимое условие сходимости, как понимаете, выполнено, что не позволяет нам отлынивать от работы.
аргумент синуса и весь общий член бесконечно малЫ. Необходимое условие сходимости, как понимаете, выполнено, что не позволяет нам отлынивать от работы.
Проведём разведку: в соответствии с замечательной эквивалентностью ![]() , мысленно отбросим синус и получим ряд
, мысленно отбросим синус и получим ряд ![]() . Ну а уж такое-то….
. Ну а уж такое-то….
Оформляем решение:
Сравним исследуемый ряд с расходящимся рядом ![]() . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
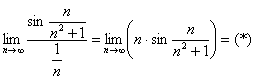
Заменим бесконечно малую эквивалентной: ![]() при
при ![]() .
.
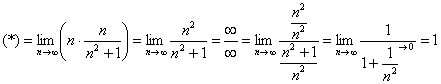
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с гармоническим рядом.
Готово.
Пример 10
Исследовать сходимость ряда
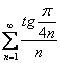
Это пример для самостоятельного решения.
Для планирования дальнейших действий в подобных примерах здОрово помогает мысленное отбрасывание синуса, арксинуса, тангенса, арктангенса. Но помните, такая возможность существует лишь при бесконечно малом аргументе, не так давно мне попался провокационный ряд:
Пример 11
Исследовать сходимость ряда
![]() .
.
Решение: здесь бесполезно использовать ограниченность арктангенса, и эквивалентность ![]() тоже не работает. Выход неожиданно прост:
тоже не работает. Выход неожиданно прост:
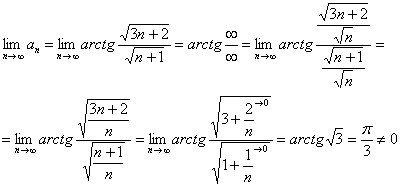
Исследуемый ряд расходится, так как не выполнен необходимый признак сходимости ряда.
Вторая причина «затыка на задании» состоит в приличной навороченности общего члена ![]() , что вызывает затруднения уже технического характера. Грубо говоря, если рассмотренные выше ряды относятся к разряду «фиг догадаешься», то эти – к категории «хрен решишь». Собственно, это и называют сложностью в «обычном» понимании. Далеко не каждый правильно разрулит несколько факториалов, степеней, корней и прочих обитателей саванны. Больше всего проблем доставляют, конечно же, факториалы:
, что вызывает затруднения уже технического характера. Грубо говоря, если рассмотренные выше ряды относятся к разряду «фиг догадаешься», то эти – к категории «хрен решишь». Собственно, это и называют сложностью в «обычном» понимании. Далеко не каждый правильно разрулит несколько факториалов, степеней, корней и прочих обитателей саванны. Больше всего проблем доставляют, конечно же, факториалы:
Пример 12
Исследовать сходимость ряда
![]()
Решение: очевидно, что нужно использовать признак Даламбера. Но ошибку проще простого допустить при разложении факториалов. Что такое факториал и как его расписать, подробно разобрано в статьях Пределы числовых последовательностей и Признак Даламбера, признаки Коши.
Как возвести факториал в степень? Легко. По правилу действий со степенями, нужно возвести в степень каждый множитель произведения:
![]()
И, конечно же, внимание и ещё раз внимание, сам-то по себе признак Даламбера работает традиционно:
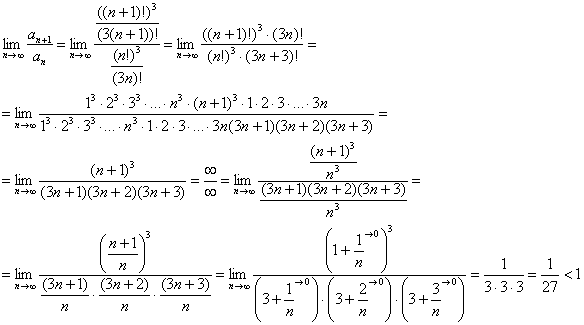
Таким образом, исследуемый ряд сходится.
Напоминаю рациональную методику устранения неопределённости ![]() : когда понятен порядок роста числителя и знаменателя – совсем не обязательно мучаться и раскрывать скобки.
: когда понятен порядок роста числителя и знаменателя – совсем не обязательно мучаться и раскрывать скобки.
Пример 13
Исследовать сходимость ряда
![]()
Зверь очень редкий, но встречается, и было бы несправедливым обойти его объективом камеры.
Что такое факториал с двойным восклицательным знаком? Факториал ![]() «накручивает» произведение положительных чётных чисел:
«накручивает» произведение положительных чётных чисел:

Аналогично, факториал ![]() «накручивает» произведение положительных нечётных чисел:
«накручивает» произведение положительных нечётных чисел:
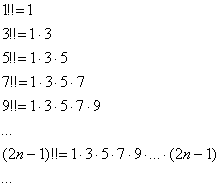
Проанализируйте, в чём состоит отличие от ![]() и
и ![]()
Пример 14
Исследовать сходимость ряда
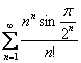
А в этом задании постарайтесь не запутаться со степенями, замечательными эквивалентностями и замечательными пределами.
Образцы решений и ответы в конце урока.
Но студент достаётся на корм не только тиграм – свою добычу выслеживают и хитрые леопарды:
Пример 15
Исследовать сходимость ряда
![]()
Решение: практически мгновенно отпадают необходимый признак сходимости, предельный признак, признаки Даламбера и Коши. Но хуже всего, что бессилен неоднократно выручавший нас признак с неравенствами. Действительно, сравнение с расходящимся рядом ![]() невозможно, так как неравенство
невозможно, так как неравенство ![]() неверно – множитель-логарифм только увеличивает знаменатель, уменьшая саму дробь
неверно – множитель-логарифм только увеличивает знаменатель, уменьшая саму дробь ![]() по отношению к дроби
по отношению к дроби ![]() . И другой глобальный вопрос: а почему мы вообще изначально уверены, что наш ряд
. И другой глобальный вопрос: а почему мы вообще изначально уверены, что наш ряд ![]() непременно обязан расходиться и его нужно сравнивать с каким-либо расходящимся рядом? Вдруг он вообще сходится?
непременно обязан расходиться и его нужно сравнивать с каким-либо расходящимся рядом? Вдруг он вообще сходится?
Интегральный признак? Несобственный интеграл ![]() навевает траурное настроение. Вот если бы у нас был ряд
навевает траурное настроение. Вот если бы у нас был ряд ![]() … тогда да. Стоп! Так и рождаются идеи. Оформляем решение в два шага:
… тогда да. Стоп! Так и рождаются идеи. Оформляем решение в два шага:
1) Сначала исследуем сходимость ряда ![]() . Используем интегральный признак:
. Используем интегральный признак:
![]()
Подынтегральная функция непрерывна на ![]()
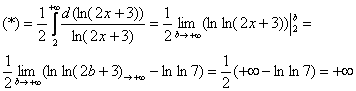
Таким образом, ряд ![]() расходится вместе с соответствующим несобственным интегралом.
расходится вместе с соответствующим несобственным интегралом.
2) Сравним наш ряд с расходящимся рядом ![]() . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
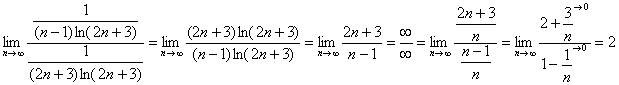
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с рядом ![]() .
.
И в таком решении нет ничего необычного или творческого – так и надо решать!
Предлагаю самостоятельно оформить следующую двухходовку:
Пример 16
Исследовать сходимость ряда
![]()
Студент с некоторым опытом в большинстве случаев сразу видит, сходится ряд или расходится, но, бывает, что хищник ловко маскируется в кустах:
Пример 17
Исследовать сходимость ряда
![]()
Решение: на первый взгляд вообще не понятно, как ведёт себя этот ряд. А если перед нами туман, то логично начать с черновой проверки необходимого условия сходимости ряда. В целях устранения неопределённости используем непотопляемый метод умножения и деления на сопряженное выражение:
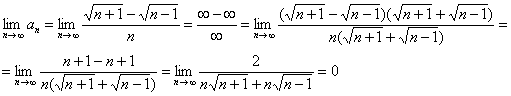
Необходимый признак сходимости не сработал, но вывел на чистую воду нашего тамбовского товарища. В результате выполненных преобразований получен эквивалентный ряд ![]() , который в свою очередь сильно напоминает сходящийся ряд
, который в свою очередь сильно напоминает сходящийся ряд ![]() .
.
Записываем чистовое решение:
Сравним данный ряд со сходящимся рядом ![]() . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
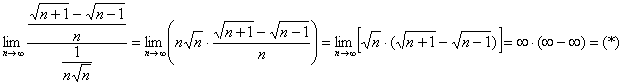
Умножим и разделим на сопряженное выражение:
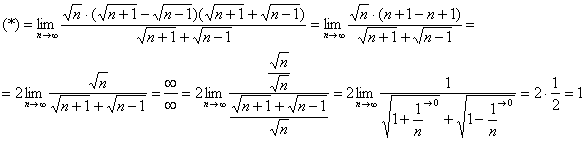
Получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом ![]() .
.
Возможно, у некоторых возник вопрос, откуда на нашем африканском сафари появились волки? Не знаю. Завезли, наверное. Следующую трофейную шкуру добывать вам:
Пример 18
Исследовать сходимость ряда
![]()
Примерный образец решения в конце урока
И, наконец, ещё одна мысль, которая в отчаянии посещает многих студентов: а не использовать ли более редкий признак сходимости ряда? Признак Раабе, признак Абеля, признак Гаусса, признак Дирихле и прочие неведомые зверушки. Идея рабочая, но в реальных примерах осуществляется очень редко. Лично я за все годы практики лишь 2-3 раза прибегнул к признаку Раабе, когда действительно ничего не помогло из стандартного арсенала. Полностью воспроизвожу ход своего экстремального квеста:
Пример 19
Исследовать сходимость ряда
![]()
Решение: безо всяких сомнений, признак Даламбера. В ходе вычислений активно использую свойства степеней, а также второй замечательный предел:
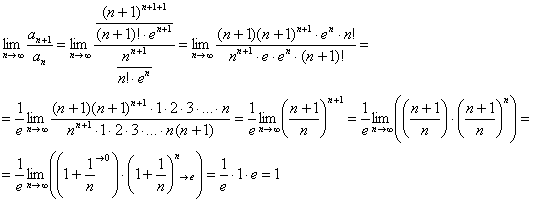
Вот тебе и раз. Признак Даламбера не дал ответа, хотя ничего не предвещало такого исхода.
Пошерстив справочник, я нашёл доказанный в теории малоизвестный предел ![]() и применил более сильный радикальный признак Коши:
и применил более сильный радикальный признак Коши:
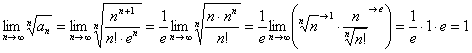
Вот тебе и два. И, главное, совершенно не понятно, сходится ряд ![]() или расходится (крайне редкая для меня ситуация). Необходимый признак сравнения? Без особых надежд – даже если немыслимым образом разберусь с порядком роста числителя и знаменателя, то это ещё не гарантирует вознаграждения.
или расходится (крайне редкая для меня ситуация). Необходимый признак сравнения? Без особых надежд – даже если немыслимым образом разберусь с порядком роста числителя и знаменателя, то это ещё не гарантирует вознаграждения.
Полный даламбер, но самое скверное, что ряд нужно решить. Нужно. Ведь это будет первый случай, когда я сдамся. И тут мне вспомнилось, что вроде существуют ещё какие-то более сильные признаки. Передо мной был уже не волк, не леопард и не тигр. Это был огромный слон, размахивающий большим хоботом. Пришлось взять в руки гранатомёт:
Признак Раабе
Рассмотрим положительный числовой ряд ![]() .
.
Если существует предел 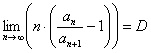 , то:
, то:
а) При ![]() ряд расходится. Причём полученное значение
ряд расходится. Причём полученное значение ![]() может быть нулевым или отрицательным
может быть нулевым или отрицательным
б) При ![]() ряд сходится. В частности, ряд сходится при
ряд сходится. В частности, ряд сходится при ![]() .
.
в) При ![]() признак Раабе не даёт ответа.
признак Раабе не даёт ответа.
Составляем предел и бережно-аккуратно упрощаем дробь:
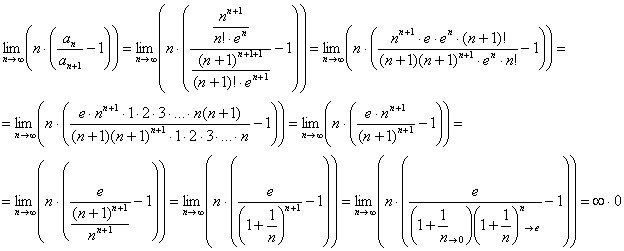
Да, картина, мягко говоря, неприятная, но я уже не удивился. Подобные пределы раскалываются с помощью правила Лопиталя, и первая мысль, как потом выяснилась, оказалось правильной. Но сначала я где-то час крутил-вертел предел «обычными» методами, однако неопределённость ![]() не желала устраняться. А ходьба по кругу, как подсказывает опыт – типичный признак того, что выбран неверный способ решения.
не желала устраняться. А ходьба по кругу, как подсказывает опыт – типичный признак того, что выбран неверный способ решения.
Пришлось обратиться к русской народной мудрости: «Если ничего не помогает, прочитайте инструкцию». И когда я открыл 2-й том Фихтенгольца, то к великой радости обнаружил исследование идентичного ряда 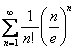 . И дальше пошло решение по образцу:
. И дальше пошло решение по образцу:
Поскольку числовая последовательность считается частным случаем функции, то в пределе 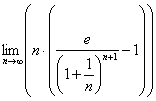 проведём замену:
проведём замену: ![]() . Если
. Если ![]() , то
, то ![]() .
.
В результате:
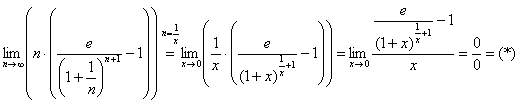
Теперь у меня предел функции и применимо правило Лопиталя. В процессе дифференцирования придётся брать производную степенно-показательной функции, которую технически удобно найти отдельно от основного решения:
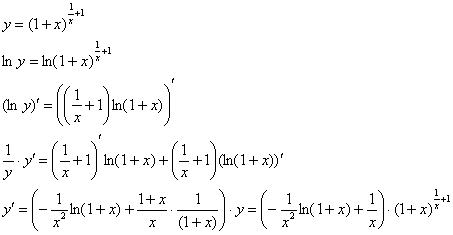
ТерпИте, раз уж сюда забрались – Бармалей в начале статьи предупреждал =) =)
Дважды использую правило Лопиталя:

Таким образом, исследуемый ряд расходится.
Потрачена уйма времени, но мои ворота устояли!
Ради интереса я вычислил 142 члена ряда в Экселе (на бОльшее не хватило вычислительной мощности) и похоже (но строго теоретически не гарантировано!), что для данного ряда не выполнен даже необходимый признак сходимости. Посмотреть эпический результат можно здесь >>> После таких злоключений не удержался от соблазна этим же любительским способом проверить и предел 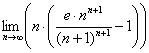 .
.
Спустя несколько лет история получила неожиданное продолжение, когда один из посетителей сайта предложил короткое и изящное решение данного примера, цитата:
«Сегодня добрались глаза и руки до вашего урока «Числовые ряды повышенной сложности», пример 19, где обсуждалось применение признака Раабе. Бессонные ночи нацедили немножечко вдохновения, и вот к какому простому способу практически моментально сделать этот пример я пришёл — формула Стирлинга.
И действительно, если воспользоваться эквивалентностью для факториала, то необходимый признак сходимости числового ряда сразу же говорит о том, что смысла дальше «марать» (простите мне мой французский) бумагу не имеет смысла. Выкладку привожу в виде картиночки:
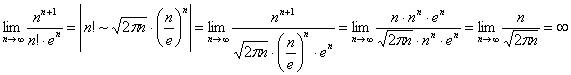 »
»
К сожалению, автор не представился =( Дополнительно поясняю, что здесь на первом шаге проведена замена ![]() на эквивалентную бесконечно большую последовательность
на эквивалентную бесконечно большую последовательность ![]() (формула Стирлинга). Ну что же, ещё раз подтвердилось моё утверждение о практической бесполезности «навороченных» признаков сравнения. Большое спасибо!
(формула Стирлинга). Ну что же, ещё раз подтвердилось моё утверждение о практической бесполезности «навороченных» признаков сравнения. Большое спасибо!
Пользуйтесь на здоровье – формула Стирлинга достаточно известна, и решение «легально»!
А это ваш слонёнок:
Пример 20
Исследовать сходимость ряда
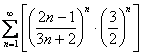
Если вы хорошо прониклись идеями данного урока, то справитесь с этим примером!
Наше путешествие завершилось на яркой ноте, и, надеюсь, у всех оставило незабываемое впечатление. Желающие продолжения банкета могут пройти на страницу Готовые задачи по высшей математике и закачать архив с дополнительными заданиями по теме.
Желаю успехов!
Решения и ответы:
Пример 2. Решение: сравним данный ряд со сходящимся рядом ![]() . Для всех натуральных номеров справедливо неравенство
. Для всех натуральных номеров справедливо неравенство ![]() , а значит, по признаку сравнения исследуемый ряд сходится вместе с рядом
, а значит, по признаку сравнения исследуемый ряд сходится вместе с рядом ![]() .
.
Пример 4. Решение: сравним данный ряд с расходящимся гармоническим рядом. Используем предельный признак сравнения:
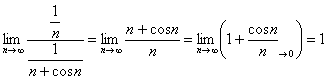
(произведение бесконечно малой ![]() на ограниченную
на ограниченную ![]() – есть бесконечно малая последовательность)
– есть бесконечно малая последовательность)
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с гармоническим рядом.
Пример 5. Решение: вынесем множитель-константу общего члена за пределы суммы, от него не зависит сходимость или расходимость ряда:
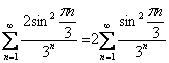
Сравним данный ряд со сходящейся бесконечно убывающей геометрической прогрессией ![]() . Последовательность
. Последовательность ![]() – ограничена:
– ограничена: ![]() , поэтому для всех натуральных номеров выполнено неравенство
, поэтому для всех натуральных номеров выполнено неравенство 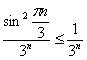 . А, значит, по признаку сравнения исследуемый ряд сходится вместе с рядом
. А, значит, по признаку сравнения исследуемый ряд сходится вместе с рядом ![]() .
.
Пример 8. Решение: сравним данный ряд с расходящимся рядом ![]() (константа-множитель общего члена не влияет на сходимость или расходимость ряда). Используем предельный признак сравнения и замечательный предел
(константа-множитель общего члена не влияет на сходимость или расходимость ряда). Используем предельный признак сравнения и замечательный предел ![]() , где
, где ![]() ::
::
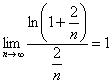
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с рядом ![]() .
.
Пример 10. Решение: сравним данный ряд со сходящимся рядом ![]() . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
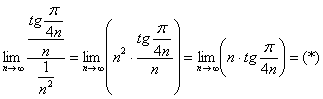
Заменим бесконечно малую эквивалентной: ![]() при
при ![]()
![]() – получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом
– получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом ![]() .
.
Пример 13. Решение: используем признак Даламбера:
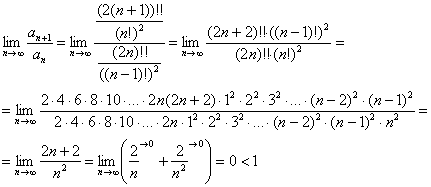
Таким образом, исследуемый ряд сходится.
Пример 14. Решение: используем признак Даламбера:
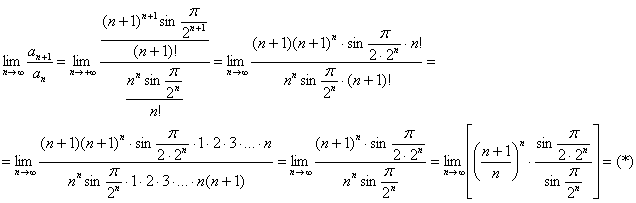
Заменим бесконечно малые эквивалентными: ![]() при
при ![]() .
.
Используем второй замечательный предел: ![]() .
.
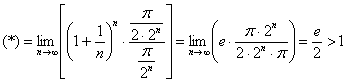
Следовательно, исследуемый ряд расходится.
Пример 16. Решение:
1) Исследуем сходимость ряда ![]() . Используем интегральный признак:
. Используем интегральный признак:
![]()
Подынтегральная функция непрерывна на ![]()
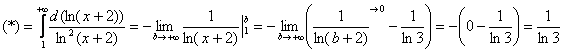
Получено конечное число, значит, ряд ![]() сходится.
сходится.
2) Сравним исследуемый ряд со сходящимся рядом ![]() . Для всех номеров выполнено неравенство
. Для всех номеров выполнено неравенство ![]() , следовательно, по признаку сравнения исследуемый ряд сходится.
, следовательно, по признаку сравнения исследуемый ряд сходится.
Пример 18. Решение: сравним данный ряд с расходящимся рядом ![]() . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
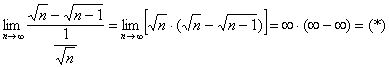
Умножим и разделим на сопряженное выражение:
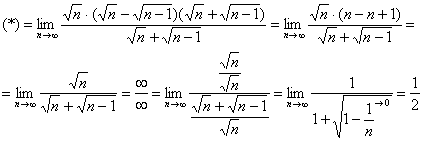
Получено конечное число, отличное от нуля, значит, исследуемый ряд расходится вместе с рядом ![]() .
.
Пример 20. Решение: проверим необходимое условие сходимости ряда. В ходе вычислений типовым приёмом организуем 2-й замечательный предел:
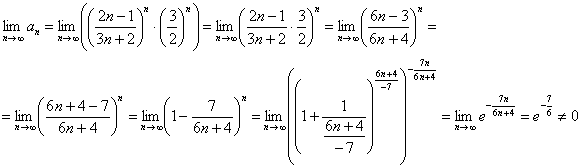
Таким образом, исследуемый ряд расходится.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright