


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Сложные пределы
В данной статье будут рассмотрены пределы повышенной сложности, и заключительный практикум по теме предназначен, прежде всего, для читателей со средним и высоким уровнем подготовки. Если ваши навыки вычисления пределов невелики или вовсе отсутствуют, пожалуйста, начните с вводного урока Пределы функций. Примеры решений. Многие методы решения пределов, о которых пойдёт речь, уже знакомы и сложность будет состоять преимущественно в технике вычислений. Кроме того, мы рассмотрим примеры с более редкими замечательными пределами, которые до сей поры были обделены моим вниманием. И, наконец, много лет спустя в курсе комплексного анализа я разобрал пределы с гиперболическими функциями (г. синусом, г. косинусом и иже с ними) – разумеется, эти приёмы работают и в нашем, действительном случае.Такие пределы почти не встречаются, но мало ли, вдруг кому потребуется…
Пока не знаю, сколько будет примеров, 15, 20 или больше, но в любом случае программа предстоит насыщенная, поэтому сразу приступим к зачистке территории:
Пример 1
Найти предел, не пользуясь правилом Лопиталя
![]()
При подстановке «единицы» в выражение под знаком предела, получается неопределённость ![]() , которая устраняется стандартным методом: числитель и знаменатель нужно разложить на множители, а затем что-нибудь сократить. Разложить на множители…. Были бы у нас многочлены второй степени – без проблем. Но как раскладывать кубические многочлены? Кратко напомню теоретический материал курса высшей алгебры:
, которая устраняется стандартным методом: числитель и знаменатель нужно разложить на множители, а затем что-нибудь сократить. Разложить на множители…. Были бы у нас многочлены второй степени – без проблем. Но как раскладывать кубические многочлены? Кратко напомню теоретический материал курса высшей алгебры:
Рассмотрим многочлен ![]() натуральной степени
натуральной степени ![]() . Если число
. Если число ![]() является корнем уравнения
является корнем уравнения ![]() , то многочлен
, то многочлен ![]() делится на многочлен
делится на многочлен ![]() без остатка. В результате деления получается многочлен
без остатка. В результате деления получается многочлен ![]() степени
степени ![]() , при этом:
, при этом: ![]() .
.
Термины точно такие же, как и для чисел:
![]() – делимое;
– делимое;
![]() – делитель;
– делитель;
![]() – частное.
– частное.
Разделить многочлен на многочлен можно по схеме Горнера, но лично я привык выполнять деление «столбиком» и сейчас мы самым подробным образом разберём этот метод. Однако сразу же оговорюсь, что в использовании схемы Горнера нет ничего предосудительного или нестандартного. Кому как удобнее, кому как понятнее.
Начнём оформлять решение и детально разберём техническую сторону вопроса:
![]()
Разложим числитель и знаменатель на множители.
Числитель: поскольку число ![]() является корнем уравнения
является корнем уравнения ![]() , то многочлен
, то многочлен ![]() делится на многочлен
делится на многочлен ![]() без остатка. Делить будем столбиком. В школе столбиком мы делили числа, и принцип деления многочленов весьма похож. Записываем начальный шаблон:
без остатка. Делить будем столбиком. В школе столбиком мы делили числа, и принцип деления многочленов весьма похож. Записываем начальный шаблон:
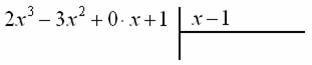
Обратите внимание на очень важную вещь: в многочлене ![]() в явном виде отсутствует «икс» в первой степени. При делении ОБЯЗАТЕЛЬНО прописываем все недостающие слагаемые, прикрепляя к ним нулевые коэффициенты.
в явном виде отсутствует «икс» в первой степени. При делении ОБЯЗАТЕЛЬНО прописываем все недостающие слагаемые, прикрепляя к ним нулевые коэффициенты.
Теперь в углу нужно разоблачить незнакомца ![]() :
:
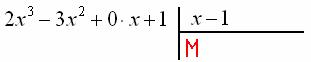
Каким он должен быть? Девчонки, признавайтесь =) …Нет-нет-нет, он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось ![]() :
:
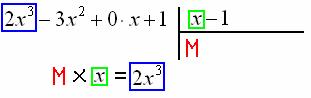
Очевидно, что данному критерию удовлетворяет ![]() . Действительно,
. Действительно, ![]() . Записываем первый трофей:
. Записываем первый трофей:
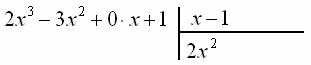
Далее нашего героя нужно умножить на делитель ![]() :
:
![]() , а результат записать во второй строке слева:
, а результат записать во второй строке слева:
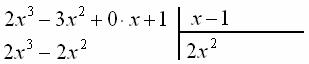
Проводим отчёркивание и из первой строки почленно вычитаем вторую строку:
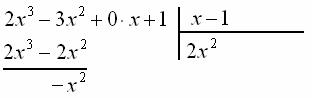
Если подробно, ![]() (ноль под чертой не пишем),
(ноль под чертой не пишем), ![]()
Сносим сверху следующее слагаемое:
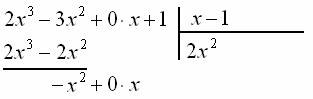
Алгоритм идёт на следующий круг. Снова ищем одночлен ![]() , он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось
, он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось ![]() :
:
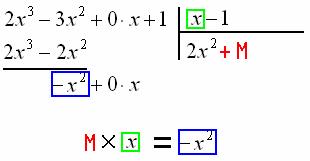
В данном случае ![]() . Рисуем его справа под чертой:
. Рисуем его справа под чертой:
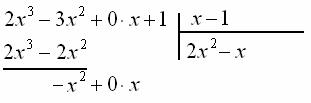
и умножаем ![]() на делитель
на делитель ![]() :
:
![]() , результат записываем в 4-ю строку:
, результат записываем в 4-ю строку:
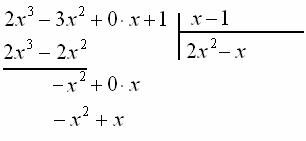
Ещё раз отчёркиваем и проводим почленное вычитание: ![]() (ноль под чертой не пишем),
(ноль под чертой не пишем), ![]() :
:
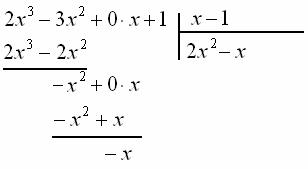
Сносим сверху последнее слагаемое:
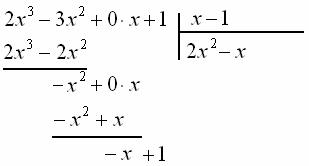
Организуем завершающий цикл. Подберём третье слагаемое ![]() , которое при умножении на «икс» даёт
, которое при умножении на «икс» даёт ![]() :
:
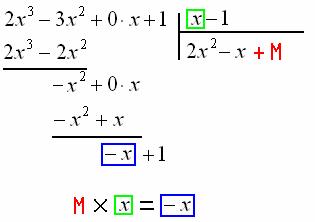
Уравнению ![]() соответствует корень
соответствует корень ![]() , который записываем справа под чертой:
, который записываем справа под чертой:
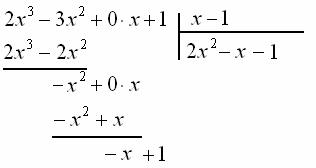
Умножаем ![]() на делитель
на делитель ![]() :
:
![]() , результат записываем в 6-ю строку:
, результат записываем в 6-ю строку:
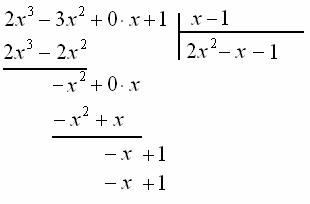
Выполняем завершающее отчёркивание и почленное вычитание:
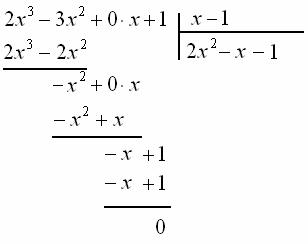
В итоге получился ноль, и это значит, что все вычисления выполнены правильно. Иными словами, многочлен ![]() поделился на
поделился на ![]() без остатка. Таким образом:
без остатка. Таким образом:
![]()
Желающие могут раскрыть скобки в правой части и убедиться, что получится исходный многочлен ![]() .
.
Рассмотренный алгоритм на самом деле не сложен, и рука набивается довольно быстро.
Знаменатель. Разборки аналогичны. Так как число ![]() является корнем уравнения
является корнем уравнения ![]() , то соответствующий многочлен делится на
, то соответствующий многочлен делится на ![]() без остатка:
без остатка:
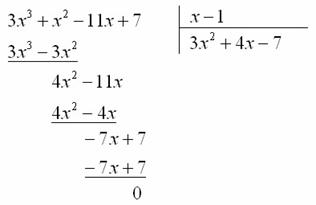
В итоге ![]()
Открываем решение и записываем всё, что нажито непосильным трудом:
![]()
Приключения продолжаются – после сокращения неопределённость не устранена. Но уже легче, квадратные трёхчлены можно разложить на множители тривиальным способом, рассмотренным на первом уроке про пределы функций. Тем не менее, в целях закрепления алгоритма продолжим деление. Да простит меня сервак =)
Числитель. Поскольку число ![]() является корнем уравнения
является корнем уравнения ![]() , то соответствующий многочлен делится на
, то соответствующий многочлен делится на ![]() без остатка. Поехали. На первом шаге подбираем
без остатка. Поехали. На первом шаге подбираем ![]() ТАКИМ образом, чтобы при его умножении на «икс» получить
ТАКИМ образом, чтобы при его умножении на «икс» получить ![]() :
:
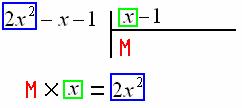
Искомое значение ![]() :
:
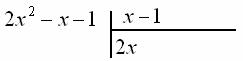
Умножаем ![]() на делитель
на делитель ![]() :
:
![]() , результат записываем слева, отчёркиваем и проводим почленное вычитание:
, результат записываем слева, отчёркиваем и проводим почленное вычитание:
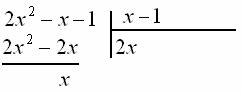
Из первой строки сносим оставшееся слагаемое:
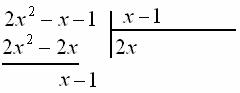
Второе значение ![]() при умножении на «икс» должно давать «икс»:
при умножении на «икс» должно давать «икс»:
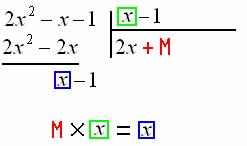
Очевидно, что ![]() :
:
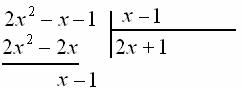
Умножаем ![]() на делитель
на делитель ![]() :
:
![]() , результат записываем ниже, отчёркиваем и проводим почленное вычитание:
, результат записываем ниже, отчёркиваем и проводим почленное вычитание:
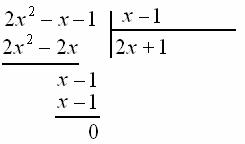
В остатке получился ноль, значит, деление выполнено верно. Таким образом:
![]()
Аналогично расправляемся со знаменателем:
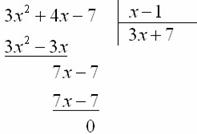
То есть ![]()
Снова открываем решение и получаем окончательный ответ:
![]()
Выполним проверку. Дважды используем правило Лопиталя:
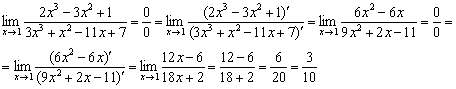
Сравните трудоёмкость двух способов решения. Думаю, теперь вам понятно, почему запрещают применять правило Лопиталя =)
Времени и сил на первый пример совсем не жалко, так как надобность делить многочлены время от времени возникает в других задачах, в частности, при нахождении нулей функции, в интегралах от дробно-рациональной функции. Поэтому с энтузиазмом отнесёмся к другим пределам…, они будут ещё длиннее =) Никто не знает, вдруг в жизни пригодится. Хах. Вспомнился заезженный анекдот в тему: если к вам на улице подошли Свидетели Иеговы, перехватите инициативу – начните им рассказывать про тройные интегралы.
Пример 2
Найти предел, не пользуясь правилом Лопиталя
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Вернёмся к другому известному способу решения пределов, повысив их сложность:
Пример 3
Найти предел, не пользуясь правилом Лопиталя
![]()
Неопределённость ![]() ликвидируется стандартным методом – умножением и делением на сопряженное выражение. Единственное отличие, приём используется два раза:
ликвидируется стандартным методом – умножением и делением на сопряженное выражение. Единственное отличие, приём используется два раза:
1) для устранения разности ![]() домножаем числитель и знаменатель на сопряженное выражение
домножаем числитель и знаменатель на сопряженное выражение ![]() ;
;
2) для устранения разности ![]() домножаем числитель и знаменатель на сопряженное выражение
домножаем числитель и знаменатель на сопряженное выражение ![]() .
.
Далее дважды используется формула ![]() . Сама техника решения подробно рассмотрена на уроке Пределы. Примеры решений.
. Сама техника решения подробно рассмотрена на уроке Пределы. Примеры решений.
Оформляем:
![]()
Оба вышеуказанных действия выгоднее выполнить «за один присест». Умножим числитель и знаменатель на сопряженные выражения:
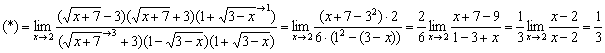
Проверим решение по правилу Лопиталя:
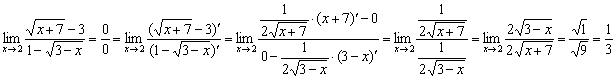
Пример 4
Найти предел, не пользуясь правилом Лопиталя
![]()
Это более сложный пример для самостоятельного решения.
Иногда в пределах рассматриваемого типа приходится использовать не только формулу разности квадратов ![]() , но и формулу разности кубов:
, но и формулу разности кубов:
Пример 5
Найти предел
![]()
Неопределённость ![]() устраняется умножением и делением на сопряженное выражение. Аналогичные, но более простые пределы мы рассмотрели в Примерах № 11-13 урока Методы решения пределов. Только здесь работает формула разности кубов:
устраняется умножением и делением на сопряженное выражение. Аналогичные, но более простые пределы мы рассмотрели в Примерах № 11-13 урока Методы решения пределов. Только здесь работает формула разности кубов:
![]()
В данном случае ![]() . И, согласно формуле, для разности
. И, согласно формуле, для разности ![]() сопряженным выражением будет вот этот вот страх:
сопряженным выражением будет вот этот вот страх:
![]()
![]()
Умножим и разделим на сопряженное выражение, чтобы использовать формулу ![]() :
:
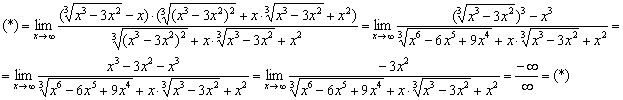
Тоже знакомая картина….
Старшая степень числителя: 2
Старшая степень знаменателя: 2
Таким образом, числитель и знаменатель одного порядка роста, и сразу можно сказать, что предел равен конечному числу.
Разделим числитель и знаменатель на ![]() :
:
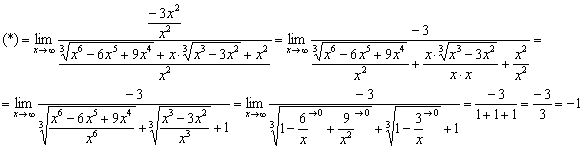
Готово.
Пример 6
Найти предел
![]()
Это пример для самостоятельного решения. После умножения/деления на сопряженное выражение и упрощений предел будет сведён к случаю Примеров № 1-3 статьи о бесконечно малых функциях. Полное решение и ответ в конце урока.
А сейчас обещанные на уроке Методы решения пределов плюшки на замену переменной. Повышенной сложности:
Пример 7
Найти предел, не пользуясь правилом Лопиталя
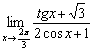
Аргумент стремится к не самому распространённому числу: ![]() , с ходу и не сообразишь, есть здесь вообще неопределённость или нет. Поэтому откроем тригонометрическую таблицу, и выпишем следующие значения:
, с ходу и не сообразишь, есть здесь вообще неопределённость или нет. Поэтому откроем тригонометрическую таблицу, и выпишем следующие значения:
![]()
Проверим предел на наличие неопределённости:
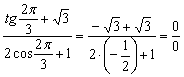
Да, действительно, два бублика.
Проведём предварительный анализ. В пределе находятся тригонометрические функции, и решение, скорее всего, сведётся к первому замечательному пределу. В этой связи напрашивается замена, после которой новая переменная будет стремиться к нулю.
Но перед заменой целесообразно провести некоторое упрощение выражения. В пределе есть тангенс, а работать с этой функцией неудобно (как и с котангенсом тоже). Таким образом, сначала лучше свести всё дело к синусам и косинусам. Пример свирепый, поэтому я закомментирую каждый шаг:
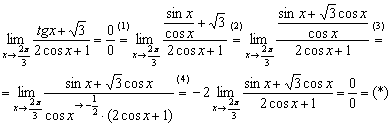
(1) Используем формулу ![]() .
.
(2) Дробь числителя приводим к общему знаменателю.
(3) Избавляемся от трёхэтажности дроби, а также от косинуса, указывая, что ![]() .
.
(4) Выносим константу 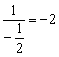 за значок предела.
за значок предела.
Неопределённость никуда не делась, но от тангенса мы избавились, что уже является небольшим достижением
Проведем замену переменной: ![]()
Если ![]() , то
, то ![]()
Ну и ещё – из замены ![]() нужно выразить:
нужно выразить: ![]() .
.
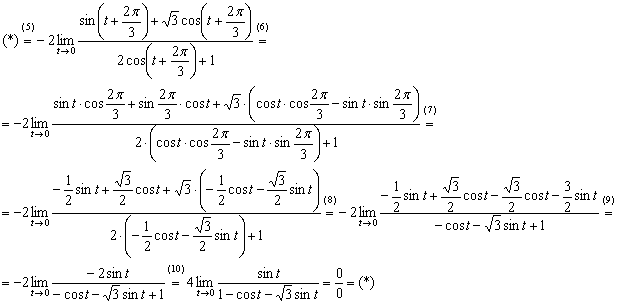
(5) Выполняем подстановку в соответствии с выполненной заменой.
(6) Используем тригонометрические формулы:
![]()
(7) Используя значения ![]() , упрощаем выражение.
, упрощаем выражение.
(8) Раскрываем скобки в числителе и знаменателе.
(9) Приводим подобные слагаемые в числителе.
(10) Константу –2 выносим за значок предела. В знаменателе переставляем слагаемые.
И снова два нуля, причём не видно как решать предел дальше…. Но если хорошенько пошуршать в тригонометрических формулах, то история закончится счастливым концом:
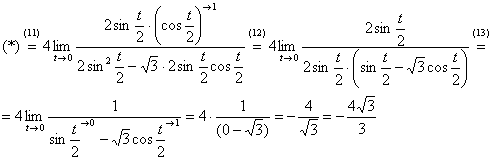
(11) Используем формулы половинного угла: ![]() . В числителе избавляемся от косинуса, указывая, что
. В числителе избавляемся от косинуса, указывая, что ![]() .
.
(12) В знаменателе выносим за скобки ![]() .
.
(13) Сокращаем числитель и знаменатель на ![]() .
.
Забавно, что всё обошлось даже без замечательного предела.
Не знаю, кто и на каком месте будет рвать себе волосы, но правило Лопиталя даёт ответ фантастически быстро:
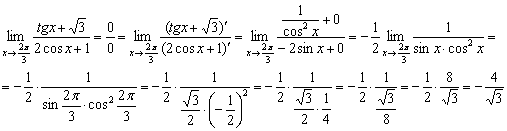
Пример 8
Найти предел, не пользуясь правилом Лопиталя
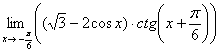
Это пример для самостоятельного решения. В тригонометрической таблице нет информации об отрицательных значениях угла. Чтобы воспользоваться таблицей, прибавляем один «оборот»: ![]() , то есть
, то есть ![]() и
и ![]() – это один и тот же угол. Таким образом:
– это один и тот же угол. Таким образом:
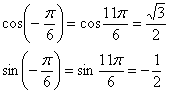
Полное решение и ответ в конце урока
Как-то незаслуженно оказались забыты степени:
Пример 9
Найти предел
![]()
Перед нами неопределённость ![]() , и решение, очевидно, нужно свести к замечательной формуле
, и решение, очевидно, нужно свести к замечательной формуле ![]() (они работают и для односторонних пределов). Но в нашем пределе нет единицы, только одинокий косинус. Что делать?
(они работают и для односторонних пределов). Но в нашем пределе нет единицы, только одинокий косинус. Что делать?
Организуем!

(1) Приводим основание степени к виду ![]() , для этого используем искусственный приём: прибавляем и вычитаем единицу. Таким образом:
, для этого используем искусственный приём: прибавляем и вычитаем единицу. Таким образом: ![]()
(2) В целях применения 2-го замечательного предела возводим основание в степень ![]() , и, чтобы ничего не изменилось – в обратную степень
, и, чтобы ничего не изменилось – в обратную степень ![]() .
.
(3) Используем замечательный предел ![]() , где
, где ![]() ..
..
(4) Теперь в показателе нужно устранить неопределённость 0:0. Сначала меняем знак в числителе: ![]() , минус выносим из предела.
, минус выносим из предела.
(5) В числителе используем формулу ![]() .
.
(6) Искусственно преобразуем знаменатель, чтобы получить два первых замечательных предела.
Очень кстати в одном примере подвернулись сразу оба замечательных предела, и после их повторения во второй части статьи рассмотрим:
Замечательные пределы с экспонентой и логарифмом
На практике чаще встречаются замечательные ![]() , особенно их частные случаи:
, особенно их частные случаи: ![]() . Предела
. Предела ![]() лично я ни разу не видел, а может быть, и видел, да не помню.
лично я ни разу не видел, а может быть, и видел, да не помню.
Иногда перечисленные пределы называют третьим, четвёртым и пятым замечательным пределом, но своё негативное отношение к избыточной нумерации я уже высказал на уроке Правила Лопиталя, поэтому пусть это будут просто замечательные пределы без номеров.
Сама техника решения мало чем отличатся от первого замечательного предела:
Пример 10
Найти предел, не пользуясь правилом Лопиталя
![]()
Используем замечательный предел ![]() . В нашем случае
. В нашем случае ![]() , и мы применяем уже знакомый искусственный приём: в знаменателе умножаем и делим на 2:
, и мы применяем уже знакомый искусственный приём: в знаменателе умножаем и делим на 2:

Вот и всё.
Короткий закусочный предел для самостоятельного решения:
Пример 11
Найти предел, не пользуясь правилом Лопиталя
![]()
Образец для сверки внизу страницы.
Заметьте, что условия не ограничивали нас в выборе действий, примеры можно было решить и через замечательные эквивалентности:
![]() (эквивалентность
(эквивалентность ![]() ).
).
Какой способ выбрать? Рекомендую всё-таки решать через замечательные пределы (конечно, если пример не дико сложный) – выглядит солиднее.
Существенная особенность пределов ![]() состоит в том, что при перестановке числителя и знаменателя результаты тоже «переворачиваются»:
состоит в том, что при перестановке числителя и знаменателя результаты тоже «переворачиваются»:
![]() ..
..
Пример 12
Найти предел, не пользуясь правилом Лопиталя
![]()
Как говорится, мал пример да заковырист….
Решаем:
![]()
На первом шаге нужно перейти к новой переменной ТАК, чтобы она стремилась к нулю.
Для этого проведём замену: ![]() , тогда:
, тогда: ![]()
Если ![]() , то
, то ![]() , и замечательные пределы, понятно, работают и для переменной «тэ»:
, и замечательные пределы, понятно, работают и для переменной «тэ»:
![]()
Самостоятельно:
Пример 13
Найти предел, не пользуясь правилом Лопиталя
![]()
Если возникли затруднения на начальном этапе, пожалуйста, вернитесь к Примеру № 9.
Разберём напоследок что-нибудь посложнее. Типовой и довольно распространённый предел:
Пример 14
Найти предел, не пользуясь правилом Лопиталя
![]()
Сначала полное решение, потом комментарии:
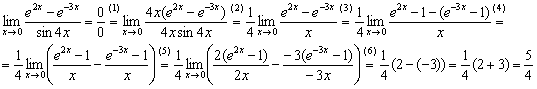
(1) На первых шагах избавляемся от синуса. Умножим числитель и знаменатель на ![]() .
.
(2) Используем первый замечательный предел ![]() , где
, где ![]() . Константу
. Константу ![]() выносим из предела.
выносим из предела.
(3) Проводим искусственное преобразование числителя. Возьмите его на заметку, разность экспонент раскручивается именно так.
(4) Почленно делим числитель на знаменатель.
(5) Числитель и знаменатель первой дроби умножаем на 2. Числитель и знаменатель второй дроби умножаем на –3.
(6) В обеих дробях используем замечательный предел ![]() , после чего остались от козлика рожки да ножки.
, после чего остались от козлика рожки да ножки.
Используя правило Лопиталя, выполним проверку:
![]()
Заключительный пример посвящен раритету ![]() . Если его не встречал я, то это не значит, что его не встретите вы. Встретите. Причём, прямо сейчас =)
. Если его не встречал я, то это не значит, что его не встретите вы. Встретите. Причём, прямо сейчас =)
Пример 15
Найти предел, не пользуясь правилом Лопиталя
![]()
Это пример для самостоятельного решения.
Всего примеров получилось таки 15, а не 20, и ваш покорный слуга постарался отобрать самые распространенные вещи. Желающие ознакомиться с другими пределами, могут закачать соответствующий архив решений в банке задач по высшей математике. Однако должен предупредить, будьте осторожнее – некоторые экземпляры не то, чтобы сильно сложные, но точно рождены воспалённым сознанием. Я постарался разобрать тему без навороченных нелепых примеров, поскольку убеждён, что студент должен мучиться с удовольствием =)
И приснится вам сегодня правило Лопиталя =)
Решения и ответы:
Пример 2
![]()
Разложим числитель и знаменатель на множители.
В числителе используем формулу суммы кубов ![]() :
:
![]()
Знаменатель:
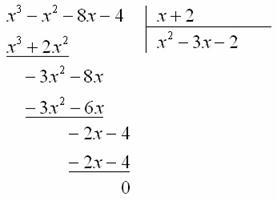
Таким образом: ![]()
![]()
Пример 4
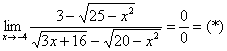
Умножим числитель и знаменатель на сопряженные выражения.
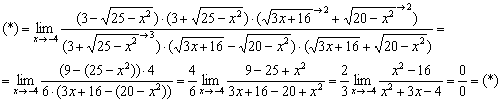
Разложим числитель и знаменатель на множители:
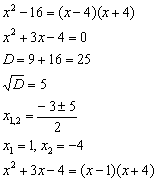
![]()
Пример 6
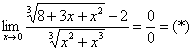
Умножим числитель и знаменатель на сопряженное выражение, используем формулу разности кубов ![]() :
:
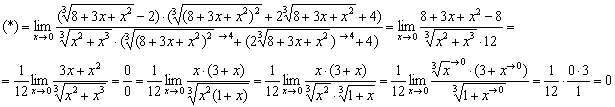
Пример 8
Используем формулу ![]() :
:
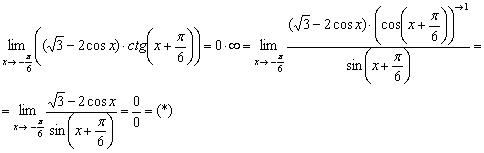
Проведём замену переменной: ![]()
Если ![]() , то
, то ![]()
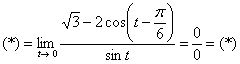
Используем тригонометрическую формулу ![]() :
:
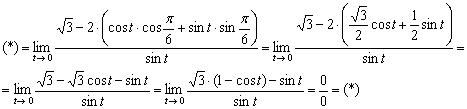
Используем формулы половинного аргумента ![]() :
:
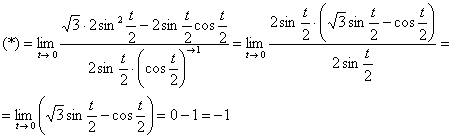
Пример 11
![]()
Умножаем числитель и знаменатель на ![]() , используем замечательный предел
, используем замечательный предел ![]() , где
, где ![]() . В конце используем 1-й замечательный предел:
. В конце используем 1-й замечательный предел:
![]()
Пример 13

Пример 15
![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright