


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Действия с матрицами
Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: умножать матрицу на число, транспонировать матрицу, складывать (вычитать) матрицы, умножать их, находить обратную матрицу. Весь материал изложен в простой и доступной форме, приведены примеры с картинками, таким образом, даже неподготовленный человек сможет подружиться с матрицами. Для самоконтроля и самопроверки есть матричный калькулятор, как говорили в стародавние времена, бесплатно, без SMS, без регистрации :) От нашего проекта.
Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться решать – проводить операции с матрицами.
Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть скальпель интенсивный
pdf-курс Матрица, определитель и зачёт!
Начнем.
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами ![]()
Пример: рассмотрим матрицу «два на три»:
![]()
Данная матрица состоит из шести элементов:
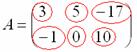
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет:
![]()
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки:
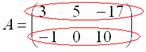
и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: 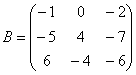 – матрица «три на три».
– матрица «три на три».
Если в матрице один столбец 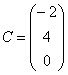 или одна строка
или одна строка ![]() , то такие матрицы также называют векторами.
, то такие матрицы также называют векторами.
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: ![]() . По существу, координаты точки
. По существу, координаты точки ![]() записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение:
записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: ![]() и
и ![]() – это две совершенно разные точки плоскости.
– это две совершенно разные точки плоскости.
Теперь переходим непосредственно к изучению действий с матрицами:
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице 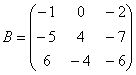 . Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
. Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак:
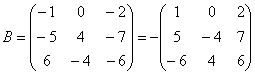
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.
Обратный пример: 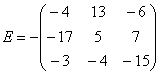 . Выглядит безобразно.
. Выглядит безобразно.
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
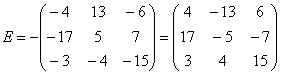
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Действие второе. Умножение матрицы на число.
Пример:
![]()
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
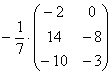 – умножение матрицы на дробь
– умножение матрицы на дробь
Сначала рассмотрим то, чего делать НЕ НАДО:
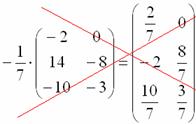
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если 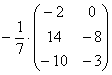 – окончательный ответ задания).
– окончательный ответ задания).
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
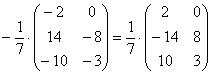
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
Пример:
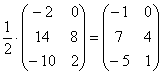
В этом случае можно и НУЖНО умножить все элементы матрицы на ![]() , так как все числа матрицы делятся на 2 без остатка.
, так как все числа матрицы делятся на 2 без остатка.
Примечание: в высшей математике чаще оперируют понятием умножение, оно включает в себя и деление. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть деление – это частный случай умножения.
3) Действие третье. Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
Пример:
Транспонировать матрицу ![]()
Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
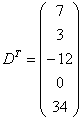 – транспонированная матрица.
– транспонированная матрица.
Транспонированная матрица обычно обозначается надстрочным индексом ![]() или штрихом справа вверху.
или штрихом справа вверху.
Пошаговый пример:
Транспонировать матрицу 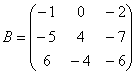
Сначала переписываем первую строку в первый столбец:
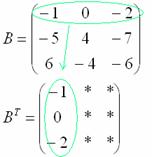
Потом переписываем вторую строку во второй столбец:
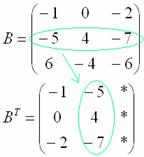
И, наконец, переписываем третью строку в третий столбец:
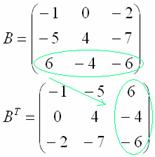
Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.
4) Действие четвертое. Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
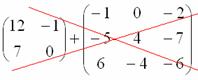
Пример:
Сложить матрицы ![]() и
и ![]()
Для того чтобы сложить матрицы, нужно сложить их соответствующие элементы:
Для разности матриц правило аналогичное, нужно найти разность соответствующих элементов.
Пример:
Найти разность матриц ![]() ,
, ![]()
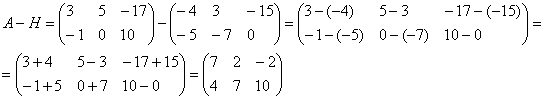
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу ![]() :
:
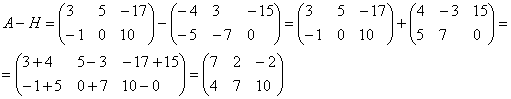
Примечание: в высшей математике в ходу понятие алгебраического сложения, которое включает в себя и вычитание. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить минус это».
5) Действие пятое. Умножение матриц.
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Какие матрицы можно умножать?
Чтобы матрицу ![]() можно было умножить на матрицу
можно было умножить на матрицу ![]() нужно, чтобы число столбцов матрицы
нужно, чтобы число столбцов матрицы ![]() равнялось числу строк матрицы
равнялось числу строк матрицы ![]() .
.
Пример:
Можно ли умножить матрицу ![]() на матрицу
на матрицу ![]() ?
?
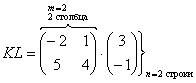
![]() , значит, умножать данные матрицы можно.
, значит, умножать данные матрицы можно.
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
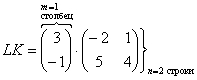
![]() , следовательно, выполнить умножение невозможно:
, следовательно, выполнить умножение невозможно:
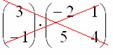
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц, ![]() и
и ![]() возможно как умножение
возможно как умножение ![]() , так и умножение
, так и умножение ![]()
Как умножить матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Пример:
Умножить матрицу ![]() на матрицу
на матрицу ![]()
Я буду сразу приводить формулу для каждого случая:
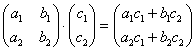 – попытайтесь сразу уловить закономерность.
– попытайтесь сразу уловить закономерность.
![]()
Пример сложнее:
Умножить матрицу ![]() на матрицу
на матрицу ![]()
Формула: 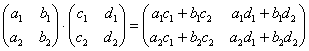
![]()
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение ![]() (правильный ответ
(правильный ответ ![]() ).
).
Обратите внимание, что ![]() ! Это почти всегда так!
! Это почти всегда так!
Таким образом, при умножении переставлять матрицы нельзя!
Если в задании предложено умножить матрицу ![]() на матрицу
на матрицу ![]() , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить матрицу 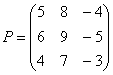 на матрицу
на матрицу 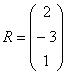
Формула очень похожа на предыдущие формулы:
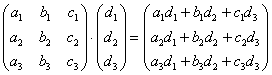
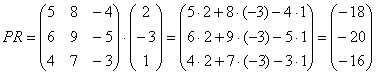
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу 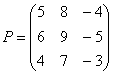 на матрицу
на матрицу 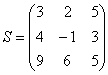
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
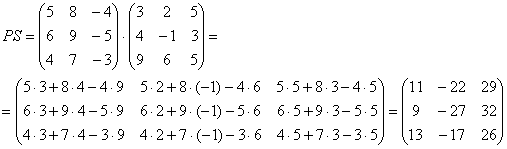
6) Действие шестое. Нахождение обратной матрицы.
Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.
А пока спектакль закончен.
После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.
Желаю успехов!
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright