


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Интегрирование по частям. Примеры решений
И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статью Неопределенный интеграл. Примеры решений) либо интеграл на замену переменной (см. статью Метод замены переменной в неопределенном интеграле) либо интеграл как раз на метод интегрирования по частям.
Для эффективного изучения темы необходимо хорошо ориентироваться в материалах двух вышеуказанных уроков. Если Вы чайник, и только-только начинаете погружение в удивительный мир интегралов, то читать далее не имеет особого смысла – следует начать с урока Неопределенный интеграл. Примеры решений.
Как всегда, под рукой должны быть: Таблица интегралов и Таблица производных. Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.
Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное. Как мы помним, нет удобной формулы:![]() . Зато есть такая:
. Зато есть такая: ![]() – формула интегрирования по частям собственной персоной. Знаю, знаю, ты одна такая – с ней мы и будем работать весь урок (уже легче).
– формула интегрирования по частям собственной персоной. Знаю, знаю, ты одна такая – с ней мы и будем работать весь урок (уже легче).
И сразу список в студию. По частям берутся интегралы следующих видов:
1) ![]() ,
, ![]() ,
, ![]() – логарифм, логарифм, умноженный на какой-нибудь многочлен.
– логарифм, логарифм, умноженный на какой-нибудь многочлен.
2) ![]() ,
,![]() – экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде
– экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде ![]() – показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е». … что-то лирической получается статья, ах да… весна же пришла.
– показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е». … что-то лирической получается статья, ах да… весна же пришла.
3) ![]() ,
, ![]() ,
, ![]() – тригонометрические функции, умноженные на какой-нибудь многочлен.
– тригонометрические функции, умноженные на какой-нибудь многочлен.
4) ![]() ,
, ![]() – обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.
– обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.
Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.
Интегралы от логарифмов
Пример 1
Найти неопределенный интеграл.
![]()
Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:
![]()
Прерываем решение на промежуточные объяснения.
Используем формулу интегрирования по частям: ![]()
Формула применяется слева направо
Смотрим на левую часть: ![]() . Очевидно, что в нашем примере
. Очевидно, что в нашем примере ![]() (и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за
(и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за ![]() , а что-то за
, а что-то за ![]() .
.
В интегралах рассматриваемого типа за ![]() обозначается логарифм либо логарифм в степени, если он обременён оной.
обозначается логарифм либо логарифм в степени, если он обременён оной.
Технически оформление решения реализуется следующим образом, в столбик записываем:
![]()
То есть за ![]() мы обозначили логарифм, а за
мы обозначили логарифм, а за ![]() – оставшуюся часть подынтегрального выражения.
– оставшуюся часть подынтегрального выражения.
Следующий этап: находим дифференциал ![]() :
:
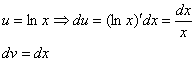
Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.
Теперь находим функцию ![]() . Для того чтобы найти функцию
. Для того чтобы найти функцию ![]() нужно проинтегрировать правую часть нижнего равенства
нужно проинтегрировать правую часть нижнего равенства ![]() :
:
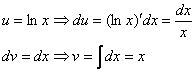
Теперь открываем наше решение и конструируем правую часть формулы: ![]() .
.
Вот кстати, и образец чистового решения с небольшими пометками:

Единственный момент, в произведении ![]() я сразу переставил местами
я сразу переставил местами ![]() и
и ![]() , так как множитель
, так как множитель ![]() принято записывать перед логарифмом.
принято записывать перед логарифмом.
Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.
Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».
Выполним проверку. Для этого нужно взять производную от ответа:
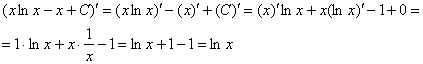
Получена исходная подынтегральная функция, значит, интеграл решён правильно.
В ходе проверки мы использовали правило дифференцирования произведения: ![]() . И это не случайно.
. И это не случайно.
Формула интегрирования по частям ![]() и формула
и формула ![]() – это два взаимно обратных правила.
– это два взаимно обратных правила.
Пример 2
Найти неопределенный интеграл.
![]()
Подынтегральная функция представляет собой произведение логарифма на многочлен.
Решаем.
![]()
Я еще один раз подробно распишу порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам урока.
Как уже говорилось, за ![]() нужно обозначить логарифм в степени. За
нужно обозначить логарифм в степени. За ![]() обозначаем оставшуюся часть подынтегрального выражения.
обозначаем оставшуюся часть подынтегрального выражения.
Записываем в столбик:
![]()
Сначала находим дифференциал ![]() :
:
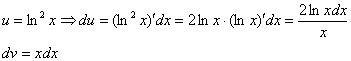
Здесь использовано правило дифференцирования сложной функции ![]() . Не случайно, на самом первом уроке темы Неопределенный интеграл. Примеры решений я акцентировал внимание на том, что для того, чтобы освоить интегралы, необходимо «набить руку» на производных. С производными придется столкнуться еще не раз.
. Не случайно, на самом первом уроке темы Неопределенный интеграл. Примеры решений я акцентировал внимание на том, что для того, чтобы освоить интегралы, необходимо «набить руку» на производных. С производными придется столкнуться еще не раз.
Теперь находим функцию ![]() , для этого интегрируем правую часть нижнего равенства
, для этого интегрируем правую часть нижнего равенства ![]() :
:
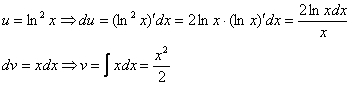
Для интегрирования мы применили простейшую табличную формулу ![]()
Теперь всё готово для применения формулы ![]() . Открываем «звёздочкой» и «конструируем» решение в соответствии с правой частью
. Открываем «звёздочкой» и «конструируем» решение в соответствии с правой частью ![]() :
:
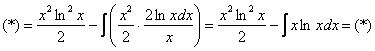
Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за ![]() в похожих ситуациях всегда обозначается логарифм.
в похожих ситуациях всегда обозначается логарифм.

Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.
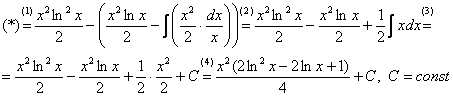
(1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус относится ко всей скобке 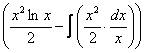 , и эти скобки нужно корректно раскрыть.
, и эти скобки нужно корректно раскрыть.
(2) Раскрываем скобки. Последний интеграл упрощаем.
(3) Берем последний интеграл.
(4) «Причесываем» ответ.
Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
А сейчас пара примеров для самостоятельного решения:
Пример 3
Найти неопределенный интеграл.
![]()
Этот пример решается методом замены переменной (или подведением под знак дифференциала)! А почему бы и нет – можете попробовать взять его по частям, получится забавная вещь.
Пример 4
Найти неопределенный интеграл.
![]()
А вот этот интеграл интегрируется по частям (обещанная дробь).
Это примеры для самостоятельного решения, решения и ответы в конце урока.
Вроде бы в примерах 3, 4 подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен. Кроме того, на втором курсе будут дифференциальные уравнения, а без опыта решения интегралов и производных делать там нечего.
По логарифмам, пожалуй, более чем достаточно. На закуску могу еще вспомнить, что студенты-технари логарифмами называют женскую грудь =). Кстати, полезно знать назубок графики основных элементарных функций: синуса, косинуса, арктангенса, экспоненты, многочленов третьей, четвертой степени и т. д. Нет, конечно, презерватив на глобус
я натягивать не буду, но теперь вы многое запомните из раздела Графики и функции =).
Интегралы от экспоненты, умноженной на многочлен
Общее правило: за ![]() всегда обозначается многочлен
всегда обозначается многочлен
Пример 5
Найти неопределенный интеграл.
![]()
Решение:
![]()
Используя знакомый алгоритм, интегрируем по частям:

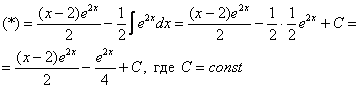
Если возникли трудности с интегралом ![]() , то следует вернуться к статье Метод замены переменной в неопределенном интеграле.
, то следует вернуться к статье Метод замены переменной в неопределенном интеграле.
Единственное, что еще можно сделать, это «причесать» ответ:
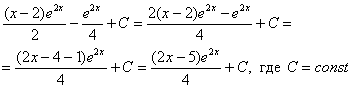
Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом ![]() или даже
или даже ![]()
То есть пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.
Пример 6
Найти неопределенный интеграл.
![]()
Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что ![]() – сложная функция.
– сложная функция.
Больше про экспоненту рассказывать особо нечего. Могу только добавить, что экспонента и натуральный логарифм взаимно-обратные функции, это я к теме занимательных графиков высшей математики =) Стоп-стоп, не волнуемся, лектор трезв.
Интегралы от тригонометрических функций, умноженных на многочлен
Общее правило: за ![]() всегда обозначается многочлен
всегда обозначается многочлен
Пример 7
Найти неопределенный интеграл.
![]()
Интегрируем по частям:
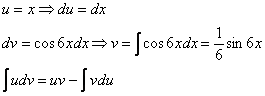
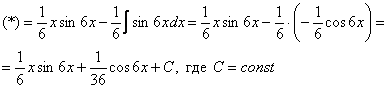
Хммм, …и комментировать нечего.
Пример 8
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения
Пример 9
Найти неопределенный интеграл
![]()
Еще один пример с дробью. Как и в двух предыдущих примерах за ![]() обозначается многочлен.
обозначается многочлен.
![]()
Интегрируем по частям:
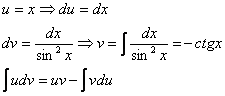
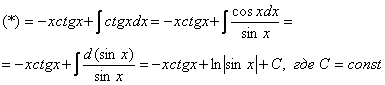
Если возникли трудности или недопонимание с нахождением интеграла ![]() , то рекомендую посетить урок Интегралы от тригонометрических функций.
, то рекомендую посетить урок Интегралы от тригонометрических функций.
Пример 10
Найти неопределенный интеграл
![]()
Это пример для самостоятельного решения.
Подсказка: перед использованием метода интегрирования по частям удобно применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….
Интегралы от обратных тригонометрических функций.
Интегралы от обратных тригонометрических функций, умноженных на многочлен
Общее правило: за ![]() всегда обозначается обратная тригонометрическая функция.
всегда обозначается обратная тригонометрическая функция.
Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»
Пример 11
Найти неопределенный интеграл.
![]()
Решаем.
![]()
Интегрируем по частям:
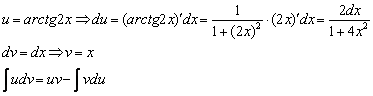
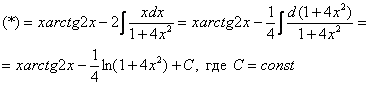
Интеграл ![]() найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде.
найден методом подведения функции под знак дифференциала, можно использовать и метод замены в «классическом» виде.
И здесь читатель задал вопрос: а куда же делся модуль под логарифмом? Ответ прост: если «начинка» логарифма неотрицательна (при любом возможном «икс»), то модуль можно не ставить. В данном примере ![]() для всех «икс», и поэтому достаточно круглых скобок. Но если вам трудно это проанализировать (да и «начинка» бывает мутная), то ставьте модуль в любом случае. Именно так я и поступил в Примере 10 урока Метод замены переменной в неопределенном интеграле. Недочёт некритичный.
для всех «икс», и поэтому достаточно круглых скобок. Но если вам трудно это проанализировать (да и «начинка» бывает мутная), то ставьте модуль в любом случае. Именно так я и поступил в Примере 10 урока Метод замены переменной в неопределенном интеграле. Недочёт некритичный.
Пример 12
Найти неопределенный интеграл.
![]()
Это пример для самостоятельного решения.
Как видите, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.
И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для маньяков желающих лучше разобраться в методе интегрирования по частям. Пример, пожалуй, будет тоже для самостоятельного решения, поскольку меня немного утомил тот логарифм в квадрате.
Пример 13
Найти неопределенный интеграл.
![]()
Что касаемо интегрирования по частям, почти всё разобрали. Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.
А сейчас, как любила говорить моя учительница по математике, пора кончать.
Желаю успехов!
Решения и ответы:
Пример 3. Решение:
![]()
Пример 4. Решение:
![]()
Интегрируем по частям:

![]()
Пример 6. Решение:
![]()
Дважды интегрируем по частям:

![]()
![]()
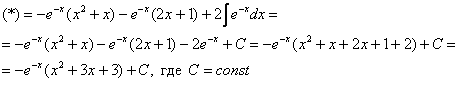
Пример 8. Решение:
![]()
Интегрируем по частям:
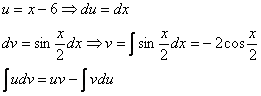
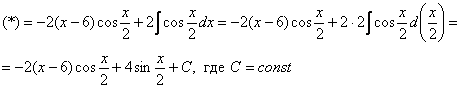
Пример 10. Решение:
![]()
Интегрируем по частям:
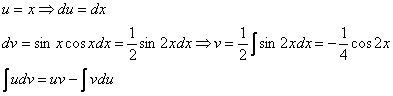
![]()
Примечание: здесь мы использовали известную тригонометрическую формулу двойного угла ![]() . Её можно было использовать и сразу:
. Её можно было использовать и сразу: ![]() , а потом интегрировать по частям.
, а потом интегрировать по частям.
Похожим способом также решаются интегралы вроде ![]() ,
, ![]() – в них нужно понизить степень синуса / косинуса с помощью соответствующих формул. Более подробно – см. Интегралы от тригонометрических функций.
– в них нужно понизить степень синуса / косинуса с помощью соответствующих формул. Более подробно – см. Интегралы от тригонометрических функций.
Пример 12. Решение:
![]()
Интегрируем по частям:
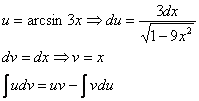
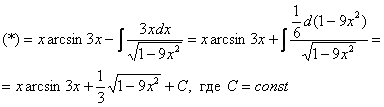
Пример 13. Решение:
![]()
Интегрируем по частям:


Примечание: если возникли трудности с интегралом ![]() , то следует посетить урок Интегрирование некоторых дробей.
, то следует посетить урок Интегрирование некоторых дробей.
Вы выполнили проверку? Может я и ошибся где… ;)
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright