Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

26. Уравнение множественной линейной регрессии

До сих пор мы рассматривали однофакторные регрессионные модели. Грубо говоря, нам был дан единственный признак-фактор  (причина), который влиял на признак-результат  (следствие). И на основании эмпирических данных (выборочных пар значений  в объеме  штук) мы оценивали тесноту корреляционной зависимости  от , а также строили линейные и нелинейные уравнения регрессии.

Но, разумеется, на зависимый показатель  часто влияют несколько или даже очень много факторов:  и наша сегодняшняя цель состоит в том, чтобы покорить множественную регрессию. Тема не очень сложная, однако, обширная и трудоёмкая, и на этом единственном уроке я разберу самые востребованные и распространённые задачи. Итак, мы научимся:

– Быстро строить уравнение множественной линейной регрессии   в MS Excel (метод наименьших квадратов), находить основные характеристики модели и проверять её качество. Этот пункт реализован в видеоролике и будет полезен для самопроверки + тем читателям, кто не погружён в статистику, а проводит лишь прикладное исследование в какой-либо предметной области (экономике, социологии, психологии, etc).

– Выполнять детальные расчёты для двухфакторной линейной модели , в том числе находить весь сопутствующий скарб: коэффициенты корреляции, детерминации, эластичности, бета; проверять значимость коэффициентов и всего уравнения. Помимо подробного мануала, смотрИте то же видео и ещё есть калькулятор, который позволяет не только автоматизировать расчёты, но и распечатать на чистовик готовое решение.

– И в конце статьи – краткая информация по расчётам модели с бОльшим количеством факторов. Формулы и добрые пожелания.

Чего НЕ будет? Не будет подробной теории и теоретизации; если вам нужен подобный материал, то некоторые источники я уже рекомендовал на уроке Модель однофакторной регрессии, копипаст:

Н. Ш. Кремер Б. А. Путко Эконометрика
И. И. Елисеева Эконометрика
и ещё мне понравилась нижегородская методичка ННГАСУ:
О. В. Любимцев О. Л. Любимцева Линейные регрессионные модели в эконометрике

Желающие без труда отыщут и более серьёзную литературу, как говорится, степень геморроя зависит от вашего аппетита :)

Ну а здесь будет всё (или почти всё) просто и популярно; …некоторые меня обвиняют в поверхностности, но пусть лучше материал усвоит максимальное количество читателей. Всё разберём на конкретном примере и простейшем случае, когда нам дано лишь два фактора:

Пример 82

По результатам выборочного исследования  торговых предприятий региона были получены отчётные данные за предыдущий год:

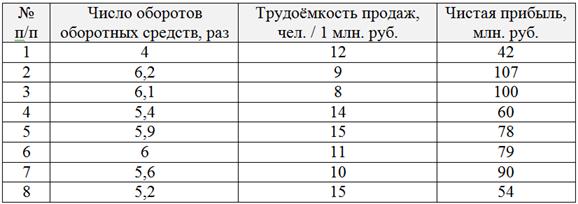
…как обычно, я не ручаюсь за правдоподобность и достоверность приведённых данных, оставляя их на совести автора методички. Но это на самом деле и не важно, у нас на повестке дня математика.

Требуется:

– обосновать и оценить влияние каждого фактора на размер чистой прибыли предприятия;

– найти уравнение двухфакторной линейной регрессии ;

– найти коэффициент множественной корреляции и детерминации;

– вычислить частные коэффициенты корреляции;

– вычислить коэффициенты эластичности;

– вычислить бета-коэффициенты;

– проверить значимость коэффициентов уравнения регрессии на уровне ;

– определить соответствующие доверительные интервалы для коэффициентов;

– проверить статистическую значимость всей модели на том же уровне ;

– спрогнозировать среднеожидаемую прибыль предприятия при  оборотах и  чел. / 1 млн. руб.

Но перед тем как решать, конечно же, нужно понять смысл предложенных показателей.

Итак, фактор  – количество оборотов оборотных средств. Что это такое? Оборотные средства – это деньги на закупку товара. Компания закупила товар и полностью продала его: таким образом, оборотные средства совершили один оборот. И предложенные в условии значения  – это количество оборотов, которые совершили оборотные средства за год. Очевидно, что чем быстрее обращаются деньги, тем больше совершается продаж и тем больше может быть прибыль предприятия. Таким образом, предполагаем прямую корреляционную зависимость прибыли предприятия  от количества оборотов оборотных средств . Следует ещё раз заметить, что это лишь общая тенденция, а не какое-то жёсткое правило, ведь есть товары с высокой и очень низкой маржой (наценкой).

Фактор второй,  – трудоёмкость продаж. К сожалению, автор задачи не уточнил данный показатель, но, судя по всему, это среднее (за год) количество персонала, которое  приходилось на один миллион выручки. Так или иначе, суть состоит в том, что чем больше людей в компании, тем больше расходы на оплату труда и тем меньше может быть её прибыль. Таким образом, предполагаем  обратную корреляционную зависимость прибыли  от трудоёмкости продаж .

Построив диаграммы рассеяния, не поленюсь:

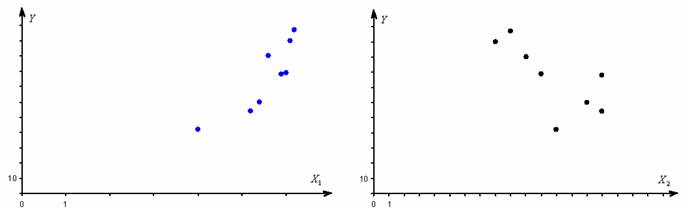
– легко уловить, что обе зависимости близкИ к линейной.

И в самом деле, вычислим линейные коэффициенты корреляции:

 – таким образом, существует сильная прямая корреляционная зависимость прибыли от количества оборотов оборотных средств;

 – и сильная обратная корреляционная зависимость прибыли от трудоёмкости продаж;

Коэффициенты можно рассчитать подробно (см. по ссылке выше), но в данном случае это «проходные» вычисления, поэтому используем стандартную экселевскую функцию:

= КОРРЕЛ(выделяем мышкой массив признака-фактора;  выделяем массив ) и жмём Enter.

Теперь нам нужно совместить обе причины в единой модели и построить выборочное уравнение двухфакторной линейной регрессии . Но не всё так просто. Для того чтобы модель множественной регрессии была качественной и вообще вменяемой, должны выполняться ряд условий. Во-первых, признаки-факторы должны быть некоррелированы. Вычислим коэффициент линейной корреляции между ними:

 – таким образом, корреляция между факторами весьма слабА и это очень хорошо. А логика здесь простА – если факторы сильно коррелированы (что называют мультиколлинеарностью), то один из них просто не имеет смысла включать в модель.

И, во-вторых, для линейной модели должны выполняться условия Гаусса-Маркова. Проверка этих условий – это отдельная большая тема, требующая местами кропотливых вычислений. Если у вас серьёзное исследование, то изучИте её более подробно (например, с помощью рекомендованной выше литературы) и воспользуйтесь специализированными статистическими программами. Ну а мы будем решать задачу в учебном режиме (по принципу «дано задание – нужно решить») и рассмотрим саму технику вычислений.

Коэффициенты уравнения регрессии   найдём методом наименьших квадратов – как решение системы:

Заполним расчётную таблицу, в нижней строке «подобьём» суммы:

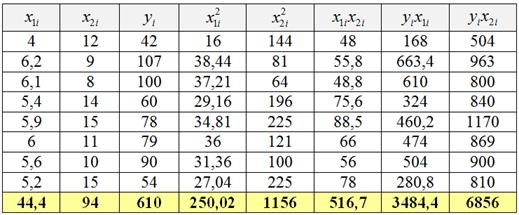
Таким образом, получаем систему:

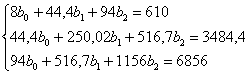
Систему решим по формулам Крамера, определители рассчитаем с помощью функции =МОПРЕД(выделяем область три на три) приложения MS Excel.

Вычислим главный определитель системы:
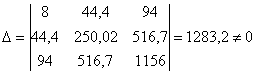, значит, система имеет единственное решение.

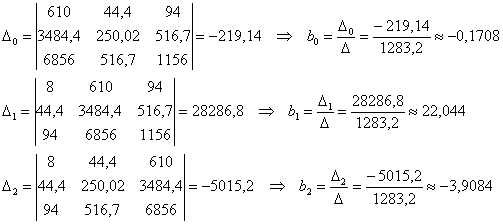
В результате, искомое уравнение регрессии:

Полученное уравнение показывает, что с ростом оборота оборотных средств на 1 оборот (при неизменной трудоёмкости) прибыль увеличивается в среднем на 22,044 млн. руб., а с увеличением трудоемкости продаж на 1 чел. / млн. руб. (при неизменном обороте) – прибыль уменьшается в среднем на 3,9084 млн. руб.

Как видите, сделанный вывод аналогичен выводу, который мы сделали для уравнения линейной регрессии с одним фактором. И многие показатели также будут похожи, в том числе и методика их быстрого расчёта – самое время посмотреть кино:

  Как быстро найти уравнение множественной регрессии? (Ютуб), и на Рутубе

Вы без труда сможете повторить все действия!  – открываем экселевский файл и решаем! Достаточно будет «черновых» расчётов, не таких красивых, как в видео. А у кого совсем нет времени и / или желания оформлять задание, есть калькулятор, который не только автоматически выполняет расчёты, но и ставит нужные выводы!

Вычислим коэффициент множественной корреляции  – он показывает силу совокупного влияния факторов  на результат . Технически это можно реализовать несколькими способами.

Чаще всего для расчёта использует найденные выше пАрные коэффициенты корреляции: 
, сведённые в симметричную матрицу :

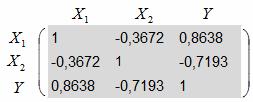
И коэффициент множественной корреляции можно рассчитать по формуле:
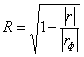, где  – определитель матрицы парных коэффициентов линейной корреляции, а  – определитель её факторной  части (без «игрековой» строки и столбца). Это общая формула (не только для двух, но и для бОльшего количества факторов).

В нашей задаче:

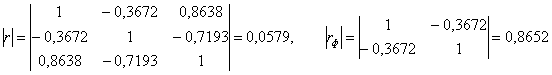
! Здесь и далее я буду местами пренебрегать знаком .

В результате:
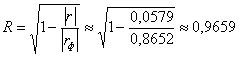 – таким образом, прибыль предприятий очень сильно зависит от предложенных в задаче факторов.

Здесь используем ту же шкалу Чеддока с той поправкой, что коэффициент множественной корреляции принимает значения  и не показывает направление зависимости (ибо факторы могут оказывать разнонаправленное действие, как в нашем случае):

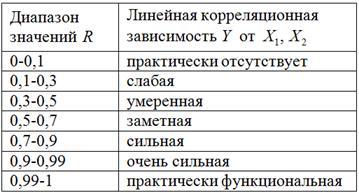
Если фактора два, то формулу можно выразить в более человеческом виде:)
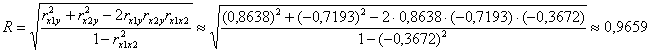 – именно такой вариант употребим в массовой практике.

Вычислим коэффициент множественной детерминации:

 – таким образом, в рамках построенной модели 93,3% вариации прибыли обусловлено числом оборотов оборотных средств и показателем трудоёмкости продаж. Остальные  вариации объясняются факторами, не учтёнными в модели.

Коэффициент множественной детерминации также можно вычислить другим, более содержательным способом, о котором я рассказал на уроке Однофакторная регрессия. Здесь подход такой же:
, где  – общая сумма квадратов, а  – остаточная сумма квадратов.

Найдём среднее значение признака-результата  млн. руб. и заполним расчётную таблицу:

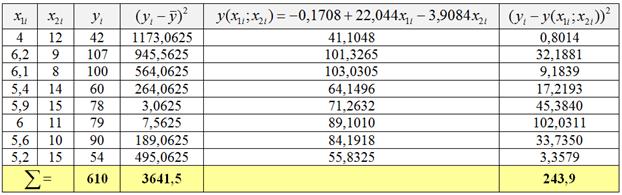
Таким образом, , в результате чего получаем тот же результат:

, с тем же выводом. Ну а для желающих понять или освежить в памяти смысл выполненных действий, ещё раз приведу ссылку на урок об однофакторной регрессии. Только сейчас случай двухфакторный, с тем же принципиальным подходом.

Вычислим частные коэффициенты корреляции. Что это такое, и чем они отличаются от парных коэффициентов ? Дело в том, что любой фактор опосредованно включает в себя (как правило) влияние других факторов, и это учитывается в парных коэффициентах. И в рамках модели множественной регрессии целесообразно исключить такое влияние, чтобы оценить «чистый» вклад каждого фактора в результат. Что и выражается частными коэффициентами корреляции

«Очистим» 1-й фактор от влияния 2-го:
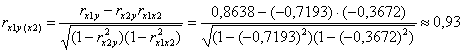 – таким образом, при устранении влияния трудоёмкости продаж чистая прибыль предприятий очень сильно зависит от числа оборотов оборотных средств.

И, наоборот, «очистим» 2-й фактор от опосредованного влияния 1-го:
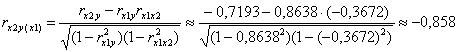 таким образом, при устранении влияния фактора оборотов оборотных средств чистая прибыль предприятий сильно зависит от трудоёмкости продаж.

Кроме того, можно найти частные коэффициенты детерминации и сделать вывод об «очищенном»  процентном вкладе каждого фактора в результат.

Но повторюсь в который раз, что все эти выводы делаются в рамках построенной модели и не являются какой-то «абсолютной истиной».

Вернёмся к полученному уравнению регрессии  и посмотрим на его коэффициенты при факторных переменных. Как мы видим, коэффициент  по модулю больше коэффициента , но это ещё не значит, что 1-й фактор оказывает бОльшее влияние на результат, чем 2-й фактор. Это лишь номинальные значения. Истинная же весомость факторов рассчитывается с помощью относительных показателей – коэффициентов средней эластичности и бета-коэффициентов, о смысле которых я рассказал ещё в начальной школе. Здесь всё аналогично.

Для расчёта этих и некоторых других показателей нам потребуется найти средние значения признаков:
 
и их исправленные стандартные отклонения:

Отклонения можно рассчитать подробно (см. по ссылке выше), я же использовал экселевскую функцию =СТАНДОТКЛОН(массив значений выборки), которая возвращается исправленные стандартные отклонения; в новой версии Экселя эта функция модифицирована: =СТАНДОТКЛОН.В(массив значений выборки).

Вычислим коэффициенты средней эластичности:

 – таким образом, при увеличении оборотов оборотных средств на 1% (при неизменной трудоёмкости продаж) чистая прибыль увеличивается в среднем на 1,6%.

 – таким образом, при увеличении трудоёмкости продаж на 1% (при неизменных оборотах) чистая прибыль уменьшается в среднем на 0,6%.

И как мы видим, прибыль действительно более чувствительна к изменению 1-го фактора, однако всё же не настолько, насколько можно было подумать, глядя на коэффициенты .

Вычислим бета-коэффициенты:

 –  таким образом, при увеличении оборотов оборотных средств на одно стандартное отклонение (при неизменной трудоёмкости продаж) чистая прибыль увеличивается примерно  на 0,69 своего стандартного отклонения.

 – таким образом, при увеличении трудоёмкости продаж на одно стандартное отклонение (при неизменных оборотах) чистая прибыль уменьшается примерно на 0,46 своего стандартного отклонения.

Что ещё раз подтверждает бОльшую весомость 1-го фактора.

Проверим значимость коэффициентов уравнения регрессии на уровне значимости При этом рассмотрим лишь ключевые факторные коэффициенты .

Алгоритм такой же, как и в однофакторной модели. Но сначала повторим краткую суть предстоящих действий. Дело в том, что уравнение  получено по результатам выборки. Но существует генеральная совокупность торговых предприятий региона и генеральное уравнение . И возникает вопрос, насколько полученные выборочные значения  далеки от истинных значений ? Насколько можно доверять выборочным результатам? (тем более выборка малА). Для проверки статистической значимости полученных значений используем аппарат статистических гипотез.

1) Проверим значимость коэффициента . Рассмотрим нулевую гипотезу  – о том, что соответствующий коэффициент генерального уравнения  равен нулю. По существу, это означает, что полученный выборочный результат  обусловлен случайностью (малой выборкой, в частности) и на самом деле чистая прибыль не зависит от количества оборотов оборотных средств.

В качестве конкурирующей рассмотрим  – гипотезу о том, что линейная корреляционная зависимость прибыли от оборотов существует.

Для проверки гипотезы  на уровне значимости  используем статистический критерий , где  – значение выборочного коэффициента при 1-й факторной переменной, а  – его  стандартная ошибка. Случайная величина  имеет распределение Стьюдента с количеством степеней свободы , где  – количество факторов модели. Их у нас два, а посему .

Для уровня значимости  и количества степеней свободы  по соответствующей таблице либо с помощью Экселя (пункт 10в) находим критическое значение двусторонней области .

Найдём наблюдаемое значение критерия . Если оно попадёт в «красную» область ( либо ), то нулевая гипотеза отвергается в пользу альтернативной; если же , то оснований отвергать нулевую гипотезу на данном уровне значимости – нет.

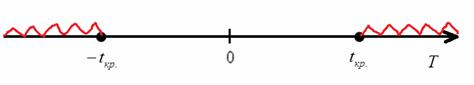
Вычислим стандартную ошибку коэффициента, учитывая, что нас -факторная модель:

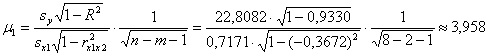
Наблюдаемое значение критерия:
 – поэтому на уровне значимости  гипотезу   отвергаем в пользу конкурирующей гипотезы .

Вывод: коэффициент  статистически значимо отличен от нуля, и полученное значение вряд ли объяснимо случайными факторами.

2) Аналогично проверяем статистическую значимость коэффициента , гипотезу  против конкурирующей гипотезы .

Вычислим стандартную ошибку 2-го коэффициента:

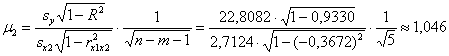
и наблюдаемое значение критерия:
 – поэтому на уровне значимости  гипотезу  отвергаем в пользу конкурирующей гипотезы .

Вывод: коэффициент  статистически значим.

Определим соответствующие доверительные интервалы.

Для первого коэффициента:

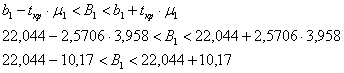
 (млн. руб.)  – таким образом, с доверительной вероятностью   данный интервал накроет истинное значение генерального коэффициента .

И аналогично для второго коэффициента:

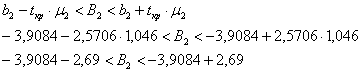
 (млн. руб.) – таким образом, с доверительной вероятностью   данный интервал накроет истинное значение генерального коэффициента

Интервалы получились грубые, конечно, ибо выборка малА.

Проверим статистическую значимость всего выборочного уравнения регрессии .  Этот вопрос эквивалентен вопросу о проверке значимости выборочного коэффициента множественной детерминации .

Рассмотрим гипотезу  – о том, что генеральный коэффициент множественной детерминации равен нулю, иными словами факторы модели вообще никак не влияют на прибыль компаний. И альтернативное утверждение  гласит о том, что такое влияние есть.

Для проверки гипотезы используем статистический критерий , где  – значение выборочного коэффициента множественной детерминации (которое от исследования к исследованию случайно), а  – количество факторных (причинных) переменных. В нашей модели фактора два: , поэтому критерий принимает вид . Эта случайная величина имеет распределение Фишера (-распределение) с количеством степеней свободы .

Для того же уровня значимости  и количества степеней свободы  по соответствующей таблице или с помощью расчётного макета (пункт 12) определяем критическое значение критерия:

Теперь вычислим наблюдаемое значение критерия. Если окажется что  (красная область) то гипотезу  на уровне значимости  отвергаем; если же , то отвергать её – оснований нет:

В нашей задаче:
 – таким образом, на уровне значимости  гипотезу  отвергаем в пользу конкурирующей гипотезы .

Вывод: коэффициент множественной детерминации  статистически значим, а значит, статистически значимо и уравнение .

И немного лирики, спрогнозируем среднеожидаемую прибыль предприятия при  оборотах и трудоёмкости  чел. / 1 млн.:

 млн. руб.

В заключение урока краткая информация о том, как рассчитать модель множественной регрессии с бОльшим количеством факторов. Пусть признак-результат зависит, например, от трёх показателей . На первом шаге нужно составить симметричную матрицу парных коэффициентов линейной корреляции:

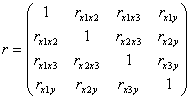
Важнейшим условием качества модели является слабая попарная коррелированность факторов (достаточно близкие к нулю значения ). В серьёзных исследованиях, кроме того, следует проверить условия Гаусса-Маркова, но это большая и обстоятельная тема, которую я оставил за кадром.

Коэффициенты регрессии   находим как решение системы:

СравнИте её с системой двухфакторной модели и уловИте закономерность в коэффициентах. Да, столбцов в расчётной таблице будет побольше, но всё подъёмно, тестовые расчёты у меня заняли порядка 15 минут.

Коэффициент множественной детерминации удобно рассчитать по формуле:
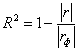, где  – определитель матрицы коэффициентов парной корреляции (см. выше), а  – определитель её факторной части (без последней строки и столбца).

Следует сказать, что у этого коэффициента есть недостаток. Дело в том, что при включении в модель любых дополнительных факторов, в том числе малозначимых или вовсе посторонних, значение  безвариантно возрастёт. И поэтому для контроля ситуации рассчитывают скорректированный коэффициент множественной детерминации:

, где  – количество факторов модели.

Теперь при добавлении явно «плохого» фактора, значение  даже уменьшится. Одним из критериев качества модели является тот факт, что значения  достаточно близки к единице и не сильно отличаются друг от друга.

Для коэффициентов частной корреляции тоже есть свои формулы, но них я не останавливаюсь, как на второстепенных. А с коэффициентами эластичности и бета-коэффициентами проблем вообще никаких – просто добавляется дополнительный коэффициент:

Вывод по каждому коэффициенту делается с оговоркой, что два других фактора неизменны.

Аналогичная ситуация в проверке значимости коэффициентов, просто проверяется ещё 3-й коэффициент.

И на посошок всё-таки общие формулы для линейной модели с «эм» факторами , корреляционная матрица:

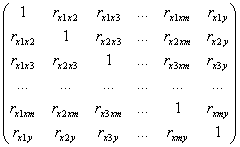
и система линейных уравнений в матричной форме:

…вроде нигде не ошибся, перепроверьте!

И я вас поздравляю! И себя тоже. Курс математической статистики на МатПрофи завершён. У него была непростая судьба – по разным обстоятельствам его создание растянулось на несколько лет. Но это свершилось, и мы здесь…. И я вам желаю всегда доводить важные дела до конца. Всего наилучшего!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте