

 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Предел функции комплексной переменной.
Определение и примеры решений
Когда зажигаются звёзды в небе ночном,
Память непрошеным гостем входит в мой дом (с)
И снова здравствуйте, с вами Александр Емелин, и с нами ностальгия…. В далёком 2010 году среди первых семи статей сайта я запостил урок о том, как решать пределы, и сейчас тема получает продолжение. Сегодня у нас ретро-вечер, поэтому зажжём свечи, возьмём в руки ручки и с трепетом вспомним первый курс, когда мы только начали изучать математический анализ….
Поскольку люди собрались тёртые, все во фраках, то сначала рассмотрим определение предела функции комплексной переменной, затем разберём пару теоретических задач и с 3-го примера зарядим практику, изучая различные методы решения пределов функции комплексной переменной. …Или переменного, как часто загадочно её величают.
По аналогии с действительным случаем, определение предела функции комплексной переменно даётся с помощью последовательностей либо на языке «эпсилон-дельта» окрестностей (по Коши). Дабы не утомлять вас теорией, я озвучу лишь второй вариант. Для этого знакомимся с понятием окрестности в комплексном случае, областями на комплексной плоскости (там же) и выдыхаем :)
Число ![]() называют пределом функции
называют пределом функции ![]() в точке
в точке ![]() , если для любой окрестности
, если для любой окрестности ![]() (заранее выбранной и сколь угодно малой) точки
(заранее выбранной и сколь угодно малой) точки ![]() , существует
, существует ![]() -окрестность точки
-окрестность точки ![]() , ТАКАЯ, что КАК ТОЛЬКО значения
, ТАКАЯ, что КАК ТОЛЬКО значения ![]() входят в эту окрестность:
входят в эту окрестность: ![]() (красная стрелка) – ТАК СРАЗУ соответствующие значения функции
(красная стрелка) – ТАК СРАЗУ соответствующие значения функции ![]() заходят в
заходят в ![]() -окрестность:
-окрестность: ![]() (синяя стрелка). «Точки входа», разумеется, могут быть в любом месте, это зависит от конкретного примера:
(синяя стрелка). «Точки входа», разумеется, могут быть в любом месте, это зависит от конкретного примера:
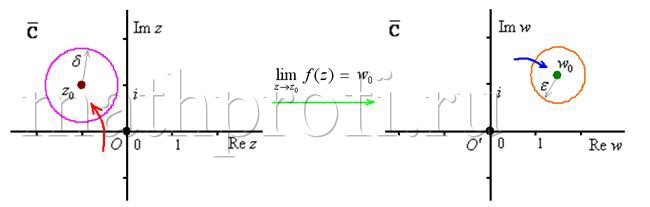
Символическое обозначение: ![]() .
.
Иными словами, если значения «зет» бесконечно близко приближаются к точке ![]() , то соответствующие значения «дубльвэ» бесконечно близко приближаются к точке
, то соответствующие значения «дубльвэ» бесконечно близко приближаются к точке ![]() , при этом траектории движений могут быть совершенно любыми. Обращаю внимание, что речь идёт лишь о приближении – в самой точке
, при этом траектории движений могут быть совершенно любыми. Обращаю внимание, что речь идёт лишь о приближении – в самой точке ![]() функция
функция ![]() может быть и не определена, т. е. значения
может быть и не определена, т. е. значения ![]() может и не существовать. В этом случае точки
может и не существовать. В этом случае точки ![]() и
и ![]() следует «выколоть».
следует «выколоть».
Если значение ![]() существует и предел функции в точке «зет нулевое»:
существует и предел функции в точке «зет нулевое»: ![]() – равен этому значению, то функция
– равен этому значению, то функция ![]() непрерывна в точке
непрерывна в точке ![]() .
.
Как видите, определение непрерывности аналогично определению в действительном случае. Его также можно сформулировать на языке «эпсилон-дельта», но я не буду.
Поскольку комплексную функцию можно записать в виде ![]() , где
, где ![]() и
и ![]() – функции двух действительных переменных, то существование конечного предела в точке
– функции двух действительных переменных, то существование конечного предела в точке ![]() :
:
![]() – эквивалентно существованию следующих двух пределов функций двух переменных:
– эквивалентно существованию следующих двух пределов функций двух переменных: ![]() . Непрерывность же функции
. Непрерывность же функции ![]() в точке
в точке ![]() эквивалентна непрерывности функций
эквивалентна непрерывности функций ![]() в точке
в точке ![]() . …Это вам справочно, для трудных жизненных ситуаций :) Ну а сейчас нас ждут более распространённые задачи:
. …Это вам справочно, для трудных жизненных ситуаций :) Ну а сейчас нас ждут более распространённые задачи:
Пример 1
С помощью определения доказать, что ![]() . Будет ли функция непрерывна в точке
. Будет ли функция непрерывна в точке ![]() ?
?
Решаем по шаблону действительного случая. Используем определение предела, запишу его кратко – читаем вслух ;)
![]()
..Есть? Теперь детально: нам нужно доказать, что для любой окрестности ![]() точки
точки ![]() существует окрестность
существует окрестность ![]() (как правило, зависящая от «эпсилон») точки
(как правило, зависящая от «эпсилон») точки ![]() , ТАКАЯ, что как только значения «зет» заходят в эту окрестность:
, ТАКАЯ, что как только значения «зет» заходят в эту окрестность: ![]() – ТАК СРАЗУ соответствующие значения «дубльвэ»
– ТАК СРАЗУ соответствующие значения «дубльвэ» ![]() оказываются в выбранной «эпсилон»-окрестности:
оказываются в выбранной «эпсилон»-окрестности: ![]() . ….Если вам не очень понятны неравенства с модулем – срочно повторяем области на комплексной плоскости.
. ….Если вам не очень понятны неравенства с модулем – срочно повторяем области на комплексной плоскости.
Рассмотрим произвольную ![]() -окрестность точки
-окрестность точки ![]() и проверим, найдётся ли
и проверим, найдётся ли ![]() -окрестность точки
-окрестность точки ![]() , такая, что из неравенства
, такая, что из неравенства ![]() следует
следует ![]() .
.
Преобразуем последнее неравенство:
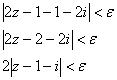
![]() – таким образом, для произвольной
– таким образом, для произвольной ![]() -окрестности точки
-окрестности точки ![]() нашлась такая окрестность
нашлась такая окрестность ![]() точки
точки ![]() .
.
Вывод: ![]() по определению.
по определению.
Проверим, будет ли функция ![]() непрерывна в точке
непрерывна в точке ![]() .
.
Во-первых, ![]() – функция определена в данной точке, это необходимое условие непрерывности.
– функция определена в данной точке, это необходимое условие непрерывности.
Более того, ![]() – предел функции в точке равен значению этой функции в данной точке.
– предел функции в точке равен значению этой функции в данной точке.
Вывод: функция непрерывна в точке по определению.
Аналогично действительному случаю, формулируется и определение бесконечного предела ![]() . Но сначала важный момент: поскольку бесконечно удалённая точка
. Но сначала важный момент: поскольку бесконечно удалённая точка ![]() единственна, то в отличие от действительного предела, здесь нет понятия «плюс» или «минус» бесконечности. Просто бесконечность! Именно так.
единственна, то в отличие от действительного предела, здесь нет понятия «плюс» или «минус» бесконечности. Просто бесконечность! Именно так.
Дадим определение бесконечного предела на языке «эпсилон-дельта». Для этого вспомним, что неравенство ![]() определяет круг с центром в начале координат радиуса
определяет круг с центром в начале координат радиуса ![]() («эпсилон-большое»). Соответственно, неравенство
(«эпсилон-большое»). Соответственно, неравенство ![]() задаёт внешнюю часть этого круга и она – есть
задаёт внешнюю часть этого круга и она – есть ![]() -окрестность бесконечно удалённой точки
-окрестность бесконечно удалённой точки ![]() . Тот факт, что значение
. Тот факт, что значение ![]() попало в эту окрестность выражается тем, что его модуль
попало в эту окрестность выражается тем, что его модуль ![]() .
.
Итак, определение![]() . Бесконечность является пределом функции
. Бесконечность является пределом функции ![]() при
при ![]() , если для любой
, если для любой ![]() -окрестности точки
-окрестности точки ![]() (заранее выбранной и сколь угодно большой) существует
(заранее выбранной и сколь угодно большой) существует ![]() -окрестность точки
-окрестность точки ![]() , ТАКАЯ, что КАК ТОЛЬКО значения
, ТАКАЯ, что КАК ТОЛЬКО значения ![]() входят в эту окрестность:
входят в эту окрестность: ![]() – ТАК СРАЗУ соответствующие значения функции
– ТАК СРАЗУ соответствующие значения функции ![]() попадают в
попадают в ![]() -окрестность:
-окрестность: ![]() .
.
Пример 2
Пользуясь определением предела, доказать, что ![]() .
.
Решение: в Примере 2 статьи об отображении линий и областей нами уже найдены действительная и мнимая части функции ![]() :
:
![]()
Составим формулу модуля значений этой функции:
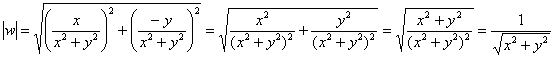
Рассмотрим произвольную ![]() -окрестность точки
-окрестность точки ![]() . Требуется доказать, что для этой окрестности существует
. Требуется доказать, что для этой окрестности существует ![]() -окрестность точки
-окрестность точки ![]() , такая, как только значения «зет» в неё попадают:
, такая, как только значения «зет» в неё попадают: ![]() – так сразу соответствующие значения «дубльвэ» входят в окрестность бесконечно удалённой точки:
– так сразу соответствующие значения «дубльвэ» входят в окрестность бесконечно удалённой точки: ![]() .
.
Из последнего неравенства выражаем ![]() – таким образом, искомая «дельта»-окрестность существует:
– таким образом, искомая «дельта»-окрестность существует: ![]() .
.
Вывод: ![]() по определению.
по определению.
Желающие могут сформулировать определения пределов ![]() , придумать и доказать простенькие примеры, а то и вовсе уединиться с теорией в отдельном кабинете. Ну а мы переходим к практическим примерам, ради которых многие заглянули к нам на огонёк.
, придумать и доказать простенькие примеры, а то и вовсе уединиться с теорией в отдельном кабинете. Ну а мы переходим к практическим примерам, ради которых многие заглянули к нам на огонёк.
На практике почти всегда предлагают конечные пределы, и методы их решения такие же, как у «обычных» пределов. Впрочем, особенности и новинки тоже будут, которые, кстати, имеют отношение и к действительному случаю. Поехали.
Во-первых, вспомним примитивный, но очень важный приём: когда мы видим любой предел, то сначала пробуем подставить в функцию предельное значение «зет»:
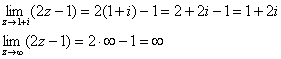
Готово! Но чаще всего, конечно, при такой подстановке нас ждёт неопределённость, которую нужно будет устранить:
Пример 3
Вычислить предел функции комплексной переменной, начнём с бороды из задачника Краснова и К:
![]()
При подстановке предельного значения ![]() в функцию обнаруживается неопределённость
в функцию обнаруживается неопределённость ![]() , поэтому прерываем решение «звёздочкой» для промежуточных действий:
, поэтому прерываем решение «звёздочкой» для промежуточных действий:
![]()
Вверху и внизу у нас находятся комплексные многочлены, и для устранения этой неопределённости следует разложить числить и знаменатель на множители, после чего что-то обязательно сократится. В нашем случае разложить нужно лишь числитель, для этого решим квадратное уравнение по стандартным формулам:
![]()
Вычислим дискриминант: ![]() , значит, уравнение имеет два комплексных корня.
, значит, уравнение имеет два комплексных корня.
Из дискриминанта извлекаются два корня: ![]() , но поскольку в формуле корней квадратного уравнения фигурируют знаки
, но поскольку в формуле корней квадратного уравнения фигурируют знаки ![]() , то достаточно рассмотреть только одно значение, возьмём
, то достаточно рассмотреть только одно значение, возьмём ![]() :
:
![]()
Таким образом, ![]() (формула там же)
(формула там же)
В результате числитель и знаменатель сокращаются на ![]() , и теперь можно смело подставлять предельное значение «зет»:
, и теперь можно смело подставлять предельное значение «зет»:
![]()
Готово. Обратите внимание, что функция ![]() не определена в точке
не определена в точке ![]() , но предел преспокойно себе существует. Ещё раз подчёркиваю, что предел – это бесконечно близкое приближение к точке, а не значение функции в ней. Ну а то, что на финише мы подставили
, но предел преспокойно себе существует. Ещё раз подчёркиваю, что предел – это бесконечно близкое приближение к точке, а не значение функции в ней. Ну а то, что на финише мы подставили ![]() и получили
и получили ![]() – всего лишь формальный технический приём.
– всего лишь формальный технический приём.
Аналогичное задание для самостоятельного решения:
Пример 4
Вычислить комплексный предел
![]()
Решаем от руки, на бумаге, лучше всего – в отдельной клетчатой тетрадке. …Помните такая была – 18 листов? :) Сверяемся с образцом в конце урока и продолжаем:
Пример 5
Вычислить предел
![]()
Если неопределённость «ноль на ноль» порождается разностью, в которой есть корень (корни), то приём тоже знакОм.
![]()
Умножим числитель и знаменатель на сопряжённое числителю выражение, чтобы воспользоваться формулой ![]() :
:
![]()
Здесь на нижнем этаже удобно сразу указать, куда стремится корень, сложить 2 + 2 и вынести результат за значок предел. В тетрадке можно обвести корень в кружочек карандашом и сделать соответствующую пометку. Ну а разность квадратов раскладываем на множители по той же формуле:
![]()
и ещё тут «крутануть» разность придётся, можно снизу, можно сверху:
![]()
Готово. Очень полезный пример в плане обилия технических приёмов…
Решаем самостоятельно, в тетрадке, и это вовсе не шутка, а настоятельная рекомендация:
Пример 6
Вычислить пределы
а) ![]()
б) ![]()
Легко видеть, что всё проходит «под копирку» действительного случая, и, конечно же, в комплексной области работают замечательные пределы:
Пример 7
![]()
И вновь неопределённость «ноль на ноль» (ибо косинус нуля – единица, синус нуля – ноль). Вспоминаем ходовые тригонометрические формулы, работающие и в комплексной области. А именно, хит ![]() :
:
![]()
Используем первый замечательный предел ![]() . Чтобы организовать сию конструкцию, причём два раза, искусственно домножаем числитель и знаменатель на
. Чтобы организовать сию конструкцию, причём два раза, искусственно домножаем числитель и знаменатель на ![]() и на
и на ![]() . Классика всегда в моде:
. Классика всегда в моде:
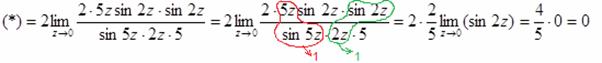
Готово. Как вариант, можно использовать замечательную эквивалентность ![]() (если
(если ![]() ):
):
![]()
Но этот подход лучше применять только в трудных случаях, так как он не слишком котируется у преподавателей. Ну, типа студент схалтурил.
Трясём стариной самостоятельно:
Пример 8
![]()
Довольно популярна в теме замена переменной:
Пример 9
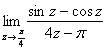
Поскольку ![]() , то имеет место быть та же неопределённость:
, то имеет место быть та же неопределённость:
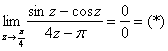
Проведём замену переменной: ![]() . Если
. Если ![]() , то
, то ![]() , и в этом-то и был смысл – если переменная стремится к нулю, то решать предел намного удобнее.
, и в этом-то и был смысл – если переменная стремится к нулю, то решать предел намного удобнее.
Ещё из замены нужно выразить «зет»:
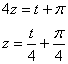
Таким образом:
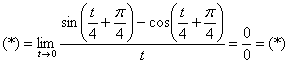
Неопределённость, естественно, никуда не делась. Используем формулы:
![]()
![]()
и проводим упрощения, используя значения ![]() :
:
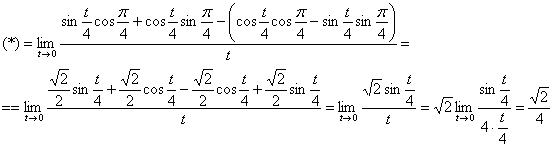
Готово. Интересный предел для самостоятельного решения…, не хочется предлагать что-то совсем простое, да пусть будет два:
Пример 10
а) ![]() – попроще,
– попроще,
б) 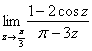 – и посложнее.
– и посложнее.
Если позабылись значения тригонометрических функций, соответствующая таблица в помощь.
Теперь переходим к новому материалу, а именно, к пределам с гиперболическими функциями. Причём, нижесказанное будет справедливо не только для комплексного, но и для частного – действительного случая. Другое дело, что действительные пределы с гиперболиками – крайняя редкость на практике, поэтому до сих пор я обходил их вниманием.
С первого урока вспоминаем, что гиперболический синус и косинус определяются через экспоненту:
![]() , откуда, к слову, сразу виднЫ очевидные значения:
, откуда, к слову, сразу виднЫ очевидные значения:
![]() , которые нужно просто-таки запомнить. Впрочем, чего тут запоминать, они такие же, как у тригонометрического синуса с косинусом.
, которые нужно просто-таки запомнить. Впрочем, чего тут запоминать, они такие же, как у тригонометрического синуса с косинусом.
И перед тем, как пилить следующие примеры, я познакомлю вас с ещё одним замечательным пределом: ![]() , «перевёртыш» в силе:
, «перевёртыш» в силе: ![]() .
.
Доказательство здесь короткое, настолько, что я даже его приведу. По определению гиперболического синуса:
![]()
Искусственно преобразуем числитель, выполняем почленное деление и сводим решение к замечательному пределу
![]() , этот приём, кстати, я уже когда-то разбирал:
, этот приём, кстати, я уже когда-то разбирал:
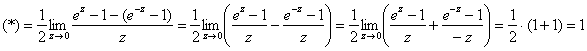
Что и требовалось доказать.
По аналогии с собратьями, внутри предела ![]() вместо «зет» может быть функция «альфа от зет», стремящаяся к нулю:
вместо «зет» может быть функция «альфа от зет», стремящаяся к нулю: ![]() .
.
Очевидно, справедлива и эквивалентность ![]() при
при ![]() .
.
Возвращаемся к практике:
Пример 11
![]()
Если в пределе одни гиперболики, то для устранения неопределённость 0/0 целесообразно использовать гиперболические формулы (с обобщением на комплексный случай), приведу самые ходовые из них:
![]() (знает каждый пионер);
(знает каждый пионер);
![]() (основное гиперболическое тождество),
(основное гиперболическое тождество),
![]() (формулы двойного аргумента);
(формулы двойного аргумента);
![]() (формулы понижения степени).
(формулы понижения степени).
В нашем пределе:
![]()
– из формулы ![]() выражаем:
выражаем:
![]()
и далее можно не постесняться использовать эквивалентность ![]() , ибо расписывать четыре замечательных предела – уже как-то чересчур:
, ибо расписывать четыре замечательных предела – уже как-то чересчур:
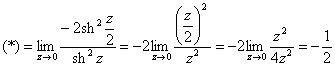
Готово. Но гораздо чаще в пределе встречается «ассорти» из тригонометрических и гиперболических функций:
Пример 12
![]()
Я намеренно выбрал очень простой пример, чтобы продемонстрировать некоторые другие идеи, которые могут быть полезны в ходе решения пределов.
Во-первых, тут сразу виден ответ. Имея в виду эквивалентности ![]() :
:
![]() – не забываем о правилах хорошего тона, представляя результат в алгебраической форме.
– не забываем о правилах хорошего тона, представляя результат в алгебраической форме.
Однако эквивалентности уместны (повторюсь), когда предел достаточно сложный, поэтому лучше организовать замечательные пределы:
![]() …, все увидели, что к чему?
…, все увидели, что к чему?
Это второй способ.
Третий подход состоит в том, чтобы решить предел с помощью рядов – разумеется, этот приём работает и в комплексном случае. Вспоминаем разложение синуса:
![]()
Поскольку у гиперболического синуса аргумент сложный, то его разложение сначала запишем с буковкой «альфа»:
![]()
В нашем примере ![]() :
:
![]()
Теперь осталось заменить синусы соответствующими рядами, вынести «зет» за скобки, сократить на «зет» и указать, что почти все члены рядов стремятся к нулю:
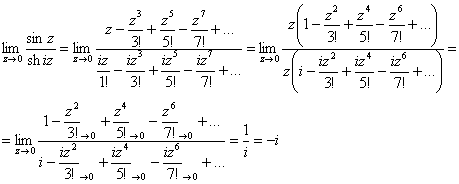
Этот метод особенно хорош, когда «начинка» предела «разношёрстная».
И, наконец, четвёртый способ, который при прочих равных я рекомендую в качестве основного. Он состоит в том, чтобы свести гиперболические функции к своим тригонометрическим собратьям, по формулам ![]() , ну или в такой версии их можно записать:
, ну или в такой версии их можно записать: ![]() .
.
В нашем примере, очевидно ![]() :
:
![]()
Готово.
Решаем самостоятельно:
Пример 13
а) ![]()
б) 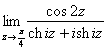
Помимо пределов функций, вам также могут встретиться пределы комплексных последовательностей, с соответствующими примерами можно ознакомиться в известной книге:
М. Л. Краснов, А. И. Киселёв, Г. И. Макаренко - Функции комплексного переменного. Задачи и примеры с подробными решениями.
Кроме того, буду рад, если вы отправите мне примеры из своих контрольных работ / методичек, которые не освещены в настоящей статье. Дело в том, что комплексные пределы – гость на практике редкий, и я привёл лишь то, что реально встретил. Поэтому предоставляю вам возможность задуть свечи.
Спасибо за присутствие, активное участие, на очереди производные.
Решения и ответы:
Пример 4. Решение:
![]()
Разложим числитель и знаменатель на множители:
![]() ,
,
используем формулу разности квадратов:
![]()
![]()
Пример 6. Решение:
а) ![]()
Умножим числитель и знаменатель на сопряженное числителю выражение:
![]()
б) ![]()
В числителе используем формулу ![]() :
:
![]()
Пример 8. Решение:
![]()
Используем формулу ![]() , избавляемся от трёхэтажности дроби и указываем, что косинус стремится к единице:
, избавляемся от трёхэтажности дроби и указываем, что косинус стремится к единице:
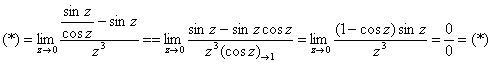
Используем первый замечательный предел ![]() , формулу
, формулу ![]() и искусственным домножением организуем ещё два замечательных предела:
и искусственным домножением организуем ещё два замечательных предела:
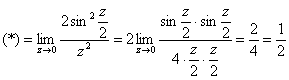
Пример 10. Решение:
а) ![]()
Проведём замену переменной: ![]() . Если
. Если ![]() , то
, то ![]() .
.
![]()
![]()
Используем формулу ![]() и первый замечательный предел:
и первый замечательный предел:
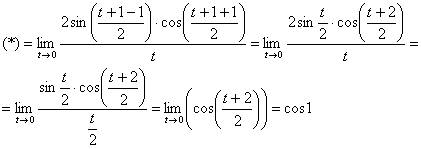
б) Поскольку ![]() , то имеем неопределённость:
, то имеем неопределённость:
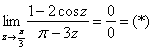
Проведём замену переменной: ![]() . Если
. Если ![]() , то
, то ![]() .
.
![]()
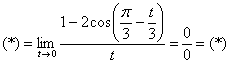
Используем формулу ![]() , затем формулы
, затем формулы ![]() и первый замечательный предел:
и первый замечательный предел:
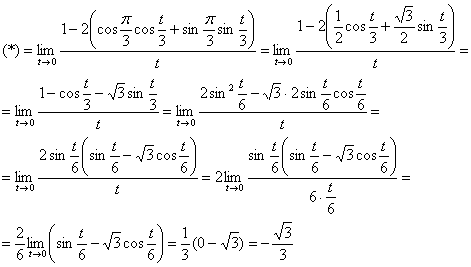
Пример 13. Решение:
а) На первом шаге удобно избавиться от гиперболического косинуса ![]() , заодно вынесем константу за значок предела:
, заодно вынесем константу за значок предела:
![]()
Заменим функции соответствующими рядами. Используем разложение:
![]() , в данном случае
, в данном случае ![]() :
:
![]()
![]()
![]() , в данном случае
, в данном случае ![]() :
:
![]()
Таким образом:
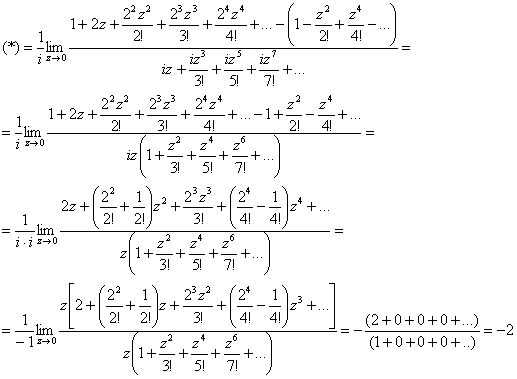
б) Тут сразу не понятно, есть неопределённость или нет, но, так или иначе, переходим к тригонометрическим функциям по формулам ![]() :
:
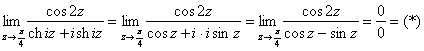
Неопределённость есть, но мы отделываемся лёгким испугом, употребляя противотревожное средство ![]() :
:
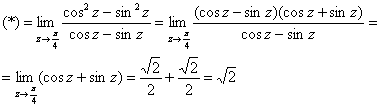
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright