


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Линии второго порядка.
Эллипс и его каноническое уравнение. Окружность
После основательной проработки прямых на плоскости продолжаем изучать геометрию двухмерного мира. Ставки удваиваются, и я приглашаю вас посетить живописную галерею эллипсов, гипербол, парабол, которые являются типичными представителями линий второго порядка. Экскурсия уже началась, и сначала краткая информация обо всей экспозиции на разных этажах музея:
Понятие алгебраической линии и её порядка
Линию на плоскости называют алгебраической, если в аффинной системе координат её уравнение имеет вид ![]() , где
, где ![]() – многочлен, состоящий из слагаемых вида
– многочлен, состоящий из слагаемых вида ![]() (
(![]() – действительное число,
– действительное число, ![]() – целые неотрицательные числа).
– целые неотрицательные числа).
Как видите, уравнение алгебраической линии не содержит синусов, косинусов, логарифмов и прочего функционального бомонда. Только «иксы» и «игреки» в целых неотрицательных степенях.
Далее под словом «линия» по умолчанию будет подразумеваться алгебраическая линия на плоскости
Порядок линии равен максимальному значению ![]() входящих в него слагаемых.
входящих в него слагаемых.
По соответствующей теореме, понятие алгебраической линии, а также её порядок не зависят от выбора аффинной системы координат, поэтому для лёгкости бытия считаем, что все последующие выкладки имеют место быть в декартовых координатах ![]() .
.
Общее уравнение линии второго порядка имеет вид ![]() , где
, где ![]() – произвольные действительные числа (
– произвольные действительные числа (![]() принято записывать с множителем-«двойкой»), причём коэффициенты
принято записывать с множителем-«двойкой»), причём коэффициенты ![]() не равны одновременно нулю.
не равны одновременно нулю.
Если ![]() , то уравнение упрощается до
, то уравнение упрощается до ![]() , и если коэффициенты
, и если коэффициенты ![]() одновременно не равны нулю, то это в точности общее уравнение «плоской» прямой, которая представляет собой линию первого порядка.
одновременно не равны нулю, то это в точности общее уравнение «плоской» прямой, которая представляет собой линию первого порядка.
Многие поняли смысл новых терминов, но, тем не менее, в целях 100%-го усвоения материала сунем пальцы в розетку. Чтобы определить порядок линии, нужно перебрать все слагаемые её уравнения и у каждого из них найти сумму степеней входящих переменных.
Например:
слагаемое ![]() содержит «икс» в 1-й степени;
содержит «икс» в 1-й степени;
слагаемое ![]() содержит «игрек» в 1-й степени;
содержит «игрек» в 1-й степени;
в слагаемом ![]() переменные отсутствуют, поэтому сумма их степеней равна нулю.
переменные отсутствуют, поэтому сумма их степеней равна нулю.
Далее из полученных чисел выбирается максимальное значение, в данном случае единица, – это и есть порядок линии.
Теперь разберёмся, почему уравнение ![]() задаёт линию второго порядка:
задаёт линию второго порядка:
слагаемое ![]() содержит «икс» во 2-й степени;
содержит «икс» во 2-й степени;
у слагаемого ![]() сумма степеней переменных: 1 + 1 = 2;
сумма степеней переменных: 1 + 1 = 2;
слагаемое ![]() содержит «игрек» во 2-й степени;
содержит «игрек» во 2-й степени;
все остальные слагаемые – меньшей степени.
Максимальное значение: 2
Если к нашему уравнению дополнительно приплюсовать, скажем, ![]() , то оно уже будет определять линию третьего порядка. Очевидно, что общий вид уравнения линии 3-го порядка содержит «полный комплект» слагаемых, сумма степеней переменных в которых равна трём:
, то оно уже будет определять линию третьего порядка. Очевидно, что общий вид уравнения линии 3-го порядка содержит «полный комплект» слагаемых, сумма степеней переменных в которых равна трём:
![]() , где коэффициенты
, где коэффициенты ![]() не равны одновременно нулю.
не равны одновременно нулю.
В том случае, если добавить одно или несколько подходящих слагаемых, которые содержат ![]() , то речь уже зайдёт о линии 4-го порядка, и т. д.
, то речь уже зайдёт о линии 4-го порядка, и т. д.
С алгебраическими линиями 3-го, 4-го и более высоких порядков нам придется столкнуться ещё не раз, в частности, при знакомстве с полярной системой координат.
Однако вернёмся к общему уравнению ![]() и вспомним его простейшие школьные вариации. В качестве примеров напрашивается парабола
и вспомним его простейшие школьные вариации. В качестве примеров напрашивается парабола ![]() , уравнение которой легко привести к общему виду
, уравнение которой легко привести к общему виду ![]() . Однако не всё так гладко….
. Однако не всё так гладко….
Существенный недостаток общего уравнения состоит в том, что почти всегда не понятно, какую линию оно задаёт. Даже в простом случае ![]() не сразу сообразишь, что это гипербола. Такие расклады хороши только на маскараде, поэтому в курсе аналитической геометрии рассматривается типовая задача приведения уравнения линии 2-го порядка к каноническому виду.
не сразу сообразишь, что это гипербола. Такие расклады хороши только на маскараде, поэтому в курсе аналитической геометрии рассматривается типовая задача приведения уравнения линии 2-го порядка к каноническому виду.
Что такое канонический вид уравнения?
Это общепринятый стандартный вид уравнения, когда в считанные секунды становится ясно, какой геометрический объект оно определяет. Кроме того, канонический вид очень удобен для решения многих практических заданий. Так, например, по каноническому уравнению ![]() «плоской» прямой, во-первых, сразу понятно, что это прямая, а во-вторых – элементарно просматривается принадлежащая ей точка
«плоской» прямой, во-первых, сразу понятно, что это прямая, а во-вторых – элементарно просматривается принадлежащая ей точка ![]() и направляющий вектор
и направляющий вектор ![]() .
.
Очевидно, что любая линия 1-го порядка представляет собой прямую. На втором же этаже нас ждёт уже не вахтёр, а гораздо более разнообразная компания из девяти статуй:
Классификация линий второго порядка
С помощью специального комплекса действий любое уравнение линии второго порядка приводится к одному из следующих видов:
(![]() и
и ![]() – положительные действительные числа)
– положительные действительные числа)
1) ![]() – каноническое уравнение эллипса;
– каноническое уравнение эллипса;
2) ![]() – каноническое уравнение гиперболы;
– каноническое уравнение гиперболы;
3) ![]() – каноническое уравнение параболы;
– каноническое уравнение параболы;
4) ![]() – мнимый эллипс;
– мнимый эллипс;
5) ![]() – пара пересекающихся прямых;
– пара пересекающихся прямых;
6) ![]() – пара мнимых пересекающихся прямых (с единственной действительной точкой пересечения в начале координат);
– пара мнимых пересекающихся прямых (с единственной действительной точкой пересечения в начале координат);
7) ![]() – пара параллельных прямых;
– пара параллельных прямых;
8) ![]() – пара мнимых параллельных прямых;
– пара мнимых параллельных прямых;
9) ![]() – пара совпавших прямых.
– пара совпавших прямых.
У ряда читателей может сложиться впечатление неполноты списка. Например, в пункте № 7 уравнение ![]() задаёт пару прямых
задаёт пару прямых ![]() , параллельных оси
, параллельных оси ![]() , и возникает вопрос: а где же уравнение
, и возникает вопрос: а где же уравнение ![]() , определяющее прямые
, определяющее прямые ![]() , параллельные оси ординат? Ответ: оно не считается каноническим. Прямые
, параллельные оси ординат? Ответ: оно не считается каноническим. Прямые ![]() представляют собой тот же самый стандартный случай
представляют собой тот же самый стандартный случай ![]() , повёрнутый на 90 градусов, и дополнительная запись
, повёрнутый на 90 градусов, и дополнительная запись ![]() в классификации избыточна, поскольку не несёт ничего принципиально нового.
в классификации избыточна, поскольку не несёт ничего принципиально нового.
Таким образом, существует девять и только девять различных видов линий 2-го порядка. Довольно часто можно встретить оборот «кривые 2-го порядка», и вот тут внимание – его нельзя применять ко всему списку. Как мы только что увидели, далеко не все из них кривые :) Но на практике в ходу как раз кривые второго порядка – эллипс, гипербола и парабола.
Сначала рассмотрим эллипс. Как обычно, я акцентирую внимание на тех моментах, которые имеют большое значение для решения задач, и если вам необходим подробный вывод формул, доказательства теорем, пожалуйста, обратитесь, например, к учебнику Базылева / Атанасяна либо Александрова.
Эллипс и его каноническое уравнение
Правописание… Пожалуйста, не повторяйте ошибок некоторых пользователей Яндекса, которых интересует «как построить эллибз», «отличие элипса от овала» и «эксцентриситет элебса». Эллипс.
Каноническое уравнение эллипса имеет вид ![]() , где
, где ![]() – положительные действительные числа, причём
– положительные действительные числа, причём ![]() . Само определение эллипса я сформулирую позже, а пока самое время отдохнуть от говорильни и решить распространённую задачу:
. Само определение эллипса я сформулирую позже, а пока самое время отдохнуть от говорильни и решить распространённую задачу:
Как построить эллипс?
Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:
Пример 1
Построить эллипс, заданный уравнением ![]()
Решение: сначала приведём уравнение к каноническому виду:
![]()
Зачем приводить? Одно из преимуществ канонического уравнения ![]() заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках
заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках ![]() . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению
. Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению ![]() .
.
В данном случае ![]() :
:
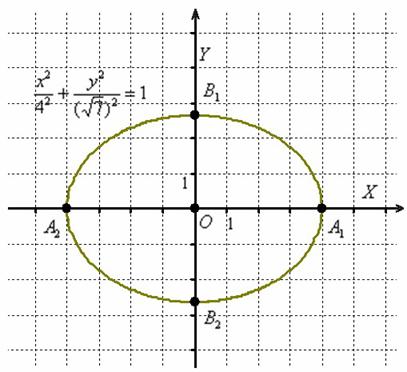
Отрезок ![]() называют большой осью эллипса;
называют большой осью эллипса;
отрезок ![]() – малой осью;
– малой осью;
число ![]() называют большой полуосью эллипса;
называют большой полуосью эллипса;
число ![]() – малой полуосью.
– малой полуосью.
в нашем примере: ![]() .
.
Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.
Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы. И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.
По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями ![]() . Как вариант, можно уменьшить масштаб и, соответственно, размеры чертежа. Но в общем случае крайне желательно найти дополнительные точки.
. Как вариант, можно уменьшить масштаб и, соответственно, размеры чертежа. Но в общем случае крайне желательно найти дополнительные точки.
Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса ![]() на черновике быстренько выражаем:
на черновике быстренько выражаем:
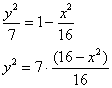
Далее уравнение распадается на две функции:
![]() – определяет верхнюю дугу эллипса;
– определяет верхнюю дугу эллипса;
![]() – определяет нижнюю дугу эллипса.
– определяет нижнюю дугу эллипса.
Заданный каноническим уравнением эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-й координатной четвертью, поэтому нам потребуется функция ![]() . Напрашивается нахождение дополнительных точек с абсциссами
. Напрашивается нахождение дополнительных точек с абсциссами ![]() . Настукаем три смс-ки на калькуляторе:
. Настукаем три смс-ки на калькуляторе:
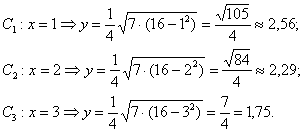
Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.
Отметим на чертеже точки ![]() (красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию:
(красный цвет), симметричные точки на остальных дугах (синий цвет) и аккуратно соединим линией всю компанию:
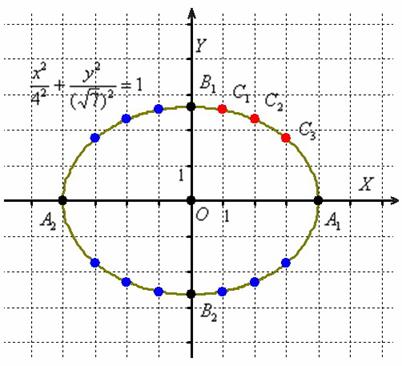
Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?
Определение эллипса. Фокусы эллипса и эксцентриситет эллипса
Эллипс – это частный случай овала. Слово «овал» не следует понимать в обывательском смысле («ребёнок нарисовал овал» и т. п.). Это математический термин, имеющий развёрнутую формулировку. Целью данного урока не является рассмотрение теории овалов и различных их видов, которым практически не уделяется внимания в стандартном курсе аналитической геометрии. И, в соответствии с более актуальными потребностями, мы сразу переходим к строгому определению эллипса:
Эллипс – это множество всех точек плоскости, сумма расстояний до каждой из которых от двух данных точек ![]() , называемых фокусами эллипса, – есть величина постоянная, численно равная длине большой оси этого эллипса:
, называемых фокусами эллипса, – есть величина постоянная, численно равная длине большой оси этого эллипса: ![]() .
.
При этом расстояния между фокусами меньше данного значения: ![]() .
.
Сейчас станет всё понятнее:
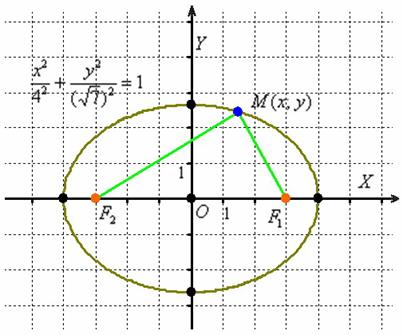
Представьте, что синяя точка «ездит» по эллипсу. Так вот, какую бы точку эллипса ![]() мы ни взяли, сумма длин отрезков
мы ни взяли, сумма длин отрезков ![]() всегда будет одной и той же:
всегда будет одной и той же:
![]()
Убедимся, что в нашем примере значение суммы ![]() действительно равно восьми. Мысленно поместите точку «эм» в правую вершину эллипса, тогда:
действительно равно восьми. Мысленно поместите точку «эм» в правую вершину эллипса, тогда: ![]() , что и требовалось проверить.
, что и требовалось проверить.
На определении эллипса основан ещё один способ его вычерчивания. Высшая математика, порой, причина напряжения и стресса, поэтому самое время провести очередной сеанс разгрузки. Пожалуйста, возьмите ватман либо большой лист картона и приколотите его к столу двумя гвоздиками. Это будут фокусы ![]() . К торчащим шляпкам гвоздей привяжите зелёную нитку и до упора оттяните её карандашом. Гриф карандаша окажется в некоторой точке
. К торчащим шляпкам гвоздей привяжите зелёную нитку и до упора оттяните её карандашом. Гриф карандаша окажется в некоторой точке ![]() , которая принадлежит эллипсу. Теперь начинайте вести карандаш по листу бумаги, сохраняя зелёную нить сильно натянутой. Продолжайте процесс до тех пор, пока не вернётесь в исходную точку… отлично… чертёж можно сдать на проверку
, которая принадлежит эллипсу. Теперь начинайте вести карандаш по листу бумаги, сохраняя зелёную нить сильно натянутой. Продолжайте процесс до тех пор, пока не вернётесь в исходную точку… отлично… чертёж можно сдать на проверку врачу преподавателю =)
Как найти фокусы эллипса?
В приведённом примере я изобразил «готовенькие» точки фокуса, и сейчас мы научимся добывать их из недр геометрии.
Если эллипс задан каноническим уравнением ![]() , то его фокусы имеют координаты
, то его фокусы имеют координаты ![]() , где
, где ![]() – это расстояние от каждого из фокусов до центра симметрии эллипса.
– это расстояние от каждого из фокусов до центра симметрии эллипса.
Вычисления проще пареной репы:
![]()
![]()
! Со значением «цэ» нельзя отождествлять конкретные координаты фокусов! Повторюсь, что ![]() – это РАССТОЯНИЕ от каждого из фокусов до центра (который в общем случае не обязан располагаться именно в начале координат).
– это РАССТОЯНИЕ от каждого из фокусов до центра (который в общем случае не обязан располагаться именно в начале координат).
И, следовательно, расстояние между фокусами ![]() тоже нельзя привязывать к каноническому положению эллипса. Иными словами, эллипс можно перенести в другое место и значение
тоже нельзя привязывать к каноническому положению эллипса. Иными словами, эллипс можно перенести в другое место и значение ![]() останется неизменным, в то время как фокусы, естественно, поменяют свои координаты. Пожалуйста, учитывайте данный момент в ходе дальнейшего изучения темы.
останется неизменным, в то время как фокусы, естественно, поменяют свои координаты. Пожалуйста, учитывайте данный момент в ходе дальнейшего изучения темы.
Едем дальше:
Эксцентриситет эллипса и его геометрический смысл
Эксцентриситетом эллипса называют отношение ![]() , которое может принимать значения в пределах
, которое может принимать значения в пределах ![]() .
.
В нашем случае: ![]()
Выясним, как форма эллипса зависит от его эксцентриситета. Для этого зафиксируем левую и правую вершины рассматриваемого эллипса, то есть значение большой полуоси ![]() будет оставаться постоянным. Тогда формула эксцентриситета примет вид:
будет оставаться постоянным. Тогда формула эксцентриситета примет вид: ![]() .
.
Начнём приближать значение эксцентриситета к единице. Это возможно только в том случае, если ![]() . Что это значит? …вспоминаем про фокусы
. Что это значит? …вспоминаем про фокусы ![]() . Это значит, что фокусы эллипса будут «разъезжаться» по оси абсцисс к боковым вершинам. И, поскольку «зелёные отрезки не резиновые», то эллипс неизбежно начнёт сплющиваться, превращаясь всё в более и более тонкую сосиску, нанизанную на ось
. Это значит, что фокусы эллипса будут «разъезжаться» по оси абсцисс к боковым вершинам. И, поскольку «зелёные отрезки не резиновые», то эллипс неизбежно начнёт сплющиваться, превращаясь всё в более и более тонкую сосиску, нанизанную на ось ![]() .
.
Таким образом, чем ближе значение эксцентриситета эллипса к единице, тем эллипс более продолговат.
Теперь смоделируем противоположный процесс: фокусы эллипса ![]() пошли навстречу друг другу, приближаясь к центру. Это означает, что значение «цэ» становится всё меньше и, соответственно, эксцентриситет стремится к нулю:
пошли навстречу друг другу, приближаясь к центру. Это означает, что значение «цэ» становится всё меньше и, соответственно, эксцентриситет стремится к нулю: ![]() .
.
При этом «зелёным отрезкам» будет, наоборот – «становиться тесно» и они начнут «выталкивать» линию эллипса вверх и вниз.
Таким образом, чем ближе значение эксцентриситета к нулю, тем эллипс больше похож на… смотрим предельный случай ![]() , когда фокусы успешно воссоединились в начале координат:
, когда фокусы успешно воссоединились в начале координат:
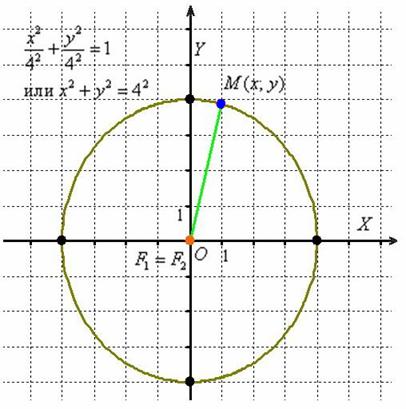
Окружность – это частный случай эллипса
Действительно, в случае равенства полуосей каноническое уравнение эллипса ![]() принимает вид
принимает вид ![]() , который рефлекторно преобразуется к
, который рефлекторно преобразуется к ![]() – хорошо известному из школы уравнению окружности с центром в начале координат радиуса «а».
– хорошо известному из школы уравнению окружности с центром в начале координат радиуса «а».
На практике чаще используют запись с «говорящей» буквой «эр»: ![]() . Радиусом называют длину отрезка
. Радиусом называют длину отрезка ![]() , при этом каждая точка
, при этом каждая точка ![]() окружности удалена от центра
окружности удалена от центра ![]() на расстояние радиуса.
на расстояние радиуса.
Заметьте, что определение эллипса остаётся полностью корректным: фокусы совпали ![]() , и сумма длин совпавших отрезков
, и сумма длин совпавших отрезков ![]() для каждой точки окружности – есть величина постоянная. Так как расстояние между фокусами
для каждой точки окружности – есть величина постоянная. Так как расстояние между фокусами ![]() , то эксцентриситет
, то эксцентриситет ![]() любой окружности равен нулю.
любой окружности равен нулю.
Строится окружность легко и быстро, достаточно вооружиться циркулем. Тем не менее, иногда бывает нужно выяснить координаты некоторых её точек, в этом случае идём знакомым путём – приводим уравнение ![]() к бодрому матановскому виду:
к бодрому матановскому виду:
![]()
![]() – функция верхней полуокружности;
– функция верхней полуокружности;
![]() – функция нижней полуокружности.
– функция нижней полуокружности.
После чего находим нужные значения, дифференцируем, интегрируем и делаем другие хорошие вещи.
Статья, конечно, носит справочный характер, но как на свете без любви прожить? Творческое задание для самостоятельного решения
Пример 2
Составить каноническое уравнение эллипса, если известен один из его фокусов ![]() и малая полуось
и малая полуось ![]() (центр находится в начале координат). Найти вершины, дополнительные точки и изобразить линию на чертеже. Вычислить эксцентриситет.
(центр находится в начале координат). Найти вершины, дополнительные точки и изобразить линию на чертеже. Вычислить эксцентриситет.
Решение и чертёж в конце урока
Добавим экшена:
Поворот и параллельный перенос эллипса
Вернёмся к каноническому уравнению эллипса ![]() , а именно, к условию
, а именно, к условию ![]() , загадка которого терзает пытливые умы ещё со времён первого упоминания о данной кривой. Вот мы рассмотрели эллипс
, загадка которого терзает пытливые умы ещё со времён первого упоминания о данной кривой. Вот мы рассмотрели эллипс ![]() , но разве на практике не может встретиться уравнение
, но разве на практике не может встретиться уравнение ![]() ? Ведь здесь
? Ведь здесь ![]() , однако, это вроде бы как тоже эллипс!
, однако, это вроде бы как тоже эллипс!
Подобное уравнение нечасто, но действительно попадается. И оно действительно определяет эллипс. Развеем мистику:
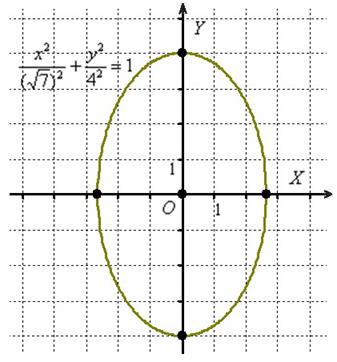
В результате построения получен наш родной эллипс, повёрнутый на 90 градусов. То есть ![]() – это неканоническая запись эллипса
– это неканоническая запись эллипса ![]() . Запись! – уравнение
. Запись! – уравнение ![]() не задаёт какой-то другой эллипс, поскольку на оси
не задаёт какой-то другой эллипс, поскольку на оси ![]() не существует точек
не существует точек ![]() (фокусов), которые бы удовлетворяли определению эллипса.
(фокусов), которые бы удовлетворяли определению эллипса.
Как быть, если такое чудо-яйцо всё-таки встретилось на жизненном пути? В том случае если вам предложено построить эллипс, то, наверное, лучше построить его в нестандартном виде. С вершинами и дополнительными точками, думаю, трудностей не возникнет. Но если вам предложено найти фокусы, эксцентриситет и т. д., то настоятельно рекомендую начать (или продолжить после чертежа) решение так:
«Повернём эллипс на 90 градусов и перепишем его уравнение ![]() в каноническом виде:
в каноническом виде: ![]() » – дальше по обычной схеме.
» – дальше по обычной схеме.
! Примечание: в теории принято поворачивать не саму фигуру, а оси! И если от вас требуется именно ПРИВЕСТИ уравнение к каноническому виду, то решение, строго говоря, следует оформить иначе: «Перейдём к новой прямоугольной системе координат ![]() , повернув координатные оси на 90 градусов против часовой стрелки, и запишем уравнение эллипса в каноническом виде:
, повернув координатные оси на 90 градусов против часовой стрелки, и запишем уравнение эллипса в каноническом виде: ![]() ».
».
Впрочем, эрудиты могут встать на скользкую дорожку путаницы, модифицировав все расчёты с учётом поворота. Но всё равно не советую. Потому что ребячество. Ведь эллипс можно повернуть и на другой угол =) Об этом мы ещё поговорим позже.
В практических задачах гораздо чаще встречается параллельный перенос эллипса:
Уравнение ![]() задаёт эллипс с большой полуосью «а», малой полуосью «бэ» и центром симметрии в точке
задаёт эллипс с большой полуосью «а», малой полуосью «бэ» и центром симметрии в точке ![]() .
.
Изобразим на чертеже эллипс ![]() . Согласно формуле:
. Согласно формуле: ![]() , то есть наш подопытный эллипс «переехал» в точку
, то есть наш подопытный эллипс «переехал» в точку ![]() :
:
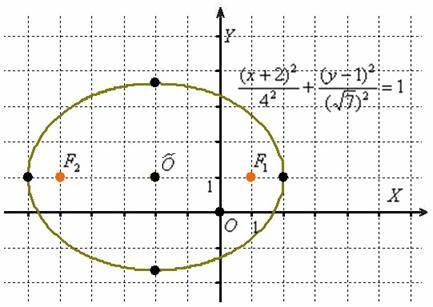
Значения ![]() остались прежними, а вот фокусы, разумеется, мигрировали, и формулы их координат нужно модифицировать поправками на соответствующие сдвиги:
остались прежними, а вот фокусы, разумеется, мигрировали, и формулы их координат нужно модифицировать поправками на соответствующие сдвиги:
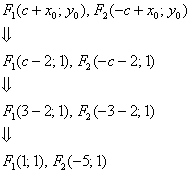
Здесь всё обходится значительно проще, чем при повороте, и если по условию не нужно приводить уравнение к каноническому виду, то лично я предпочту оставить его в виде ![]() . Что делать, если нужно приводить? «Чайникам» в большинстве случаев простят фразу: «Осуществим параллельный перенос эллипса в начало координат и перепишем уравнение
. Что делать, если нужно приводить? «Чайникам» в большинстве случаев простят фразу: «Осуществим параллельный перенос эллипса в начало координат и перепишем уравнение ![]() в каноническом виде:
в каноническом виде: ![]() ». Но академический подход предполагает параллельный перенос не самой фигуры, а системы координат! Поэтому людям, изучающим высшую математику по профилю и/или углублённо, гораздо лучше завернуть примерно следующее: «С помощью параллельного переноса исходной системы координат перейдём к новой прямоугольной системе координат
». Но академический подход предполагает параллельный перенос не самой фигуры, а системы координат! Поэтому людям, изучающим высшую математику по профилю и/или углублённо, гораздо лучше завернуть примерно следующее: «С помощью параллельного переноса исходной системы координат перейдём к новой прямоугольной системе координат ![]() с началом в точке
с началом в точке ![]() и запишем уравнение эллипса в каноническом виде
и запишем уравнение эллипса в каноническом виде ![]() ».
».
На самом деле упрощенная версия формулы нам знакома ещё со школьных времён:
Уравнение ![]() задаёт окружность радиуса
задаёт окружность радиуса ![]() с центром в точке
с центром в точке ![]() .
.
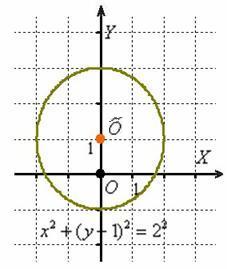
Освежая ностальгические воспоминания, изобразим на чертеже окружность, заданную уравнением ![]() :
:
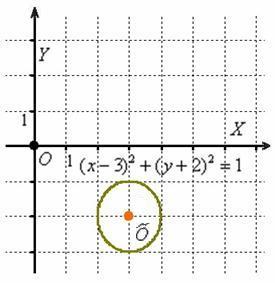
В исследовательских целях приведём наше уравнение к общему виду, выполнив возведение в квадрат и приведение подобных слагаемых:
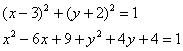
![]() – как правило, в таком обличье оно и встречается в природе.
– как правило, в таком обличье оно и встречается в природе.
Таким образом, в практических задачах часто предварительно нужно выполнить обратное действие – выделить полные квадраты. Данный приём подробно разобран на уроках о геометрических преобразованиях графиков и интегрировании дробей. Хотя следующий простой пример не должен вызвать у вас затруднений даже без отработки данного метода:
Пример 3
Построить график линии, заданной уравнением ![]()
Решение и чертёж в конце урока.
На практике эллипс (как и другие линии) может быть одновременно повёрнут на любой угол относительно своего канонического положения и перенесен в любую точку, отличную от начала координат. В таком случае решается типовая задача приведения линии 2-го порядка к каноническому виду, к которой я потихоньку начал вас готовить уже сегодня.
Ну а пока самое время перейти ко второй части лекции, где жертвами станут гипербола и парабола.
Решения и ответы:
Пример 2. Решение: поскольку фокусы канонически расположенного эллипса имеют координаты ![]() , то расстояние от каждого из фокусов до начала координат равно:
, то расстояние от каждого из фокусов до начала координат равно: ![]() .
.
По условию известно значение ![]() , из соотношения
, из соотношения ![]() находим:
находим:
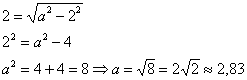
Запишем каноническое уравнение эллипса:
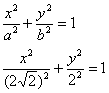
Вершины эллипса расположены в точках ![]() .
.
Найдём дополнительные точки:
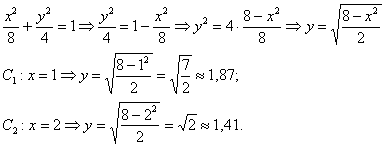
Выполним чертёж:
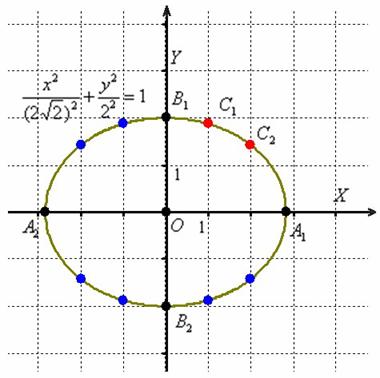
Вычислим эксцентриситет: ![]()
Пример 3. Решение: выделим полный квадрат:
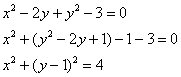
![]() – окружность радиуса
– окружность радиуса ![]() с центром в точке
с центром в точке ![]() .
.
Выполним чертёж:
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright