


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Производная по определению (через предел). Примеры решений
Когда человек сделал первые самостоятельные шаги в изучении математического анализа и начинает задавать неудобные вопросы, то уже не так-то просто отделаться фразой, что «дифференциальное исчисление найдено в капусте». Поэтому настало время набраться решимости и раскрыть тайну появления на свет таблицы производных и правил дифференцирования. Начало положено в статье о смысле производной, которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме. Этот же урок носит ярко выраженную практическую направленность, более того, рассматриваемые ниже примеры, в принципе, можно освоить и чисто формально (например, когда нет времени / желания вникать в суть производной). Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий: Как найти производную? и Производная сложной функции.
Но без чего-чего сейчас точно не обойтись, так это без пределов функций. Вы должны ПОНИМАТЬ, что такое предел и уметь решать их, как минимум, на среднем уровне. А всё потому, что производная функции ![]() в точке
в точке ![]() определяется формулой:
определяется формулой:
![]()
Напоминаю обозначения и термины:
![]() называют приращением аргумента;
называют приращением аргумента;
![]() – приращением функции;
– приращением функции;
![]() – это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
– это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
Очевидно, что ![]() является «динамической» переменной,
является «динамической» переменной, ![]() – константой и результат вычисления предела
– константой и результат вычисления предела ![]() – числом (иногда – «плюс» либо «минус» бесконечностью).
– числом (иногда – «плюс» либо «минус» бесконечностью).
В качестве точки ![]() можно рассмотреть ЛЮБОЕ значение
можно рассмотреть ЛЮБОЕ значение ![]() , принадлежащее области определения функции
, принадлежащее области определения функции ![]() , в котором существует производная.
, в котором существует производная.
! Примечание: оговорка «в котором существует производная» – в общем случае существенна! Так, например, точка ![]() хоть и входит в область определения функции
хоть и входит в область определения функции ![]() , но производной
, но производной ![]() там не существует. Поэтому формула
там не существует. Поэтому формула ![]() не применима в точке
не применима в точке ![]() , и укороченная формулировка без оговорки будет некорректна. Аналогичные факты справедливы и для других функций с «обрывами» графика, в частности, для арксинуса и арккосинуса.
, и укороченная формулировка без оговорки будет некорректна. Аналогичные факты справедливы и для других функций с «обрывами» графика, в частности, для арксинуса и арккосинуса.
Таким образом, после замены ![]() , получаем вторую рабочую формулу:
, получаем вторую рабочую формулу:
![]()
Обратите внимание на коварное обстоятельство, которое может запутать чайника: в данном пределе «икс», будучи сам независимой переменной, исполняет роль статиста, а «динамику» задаёт опять же приращение ![]() . Результатом вычисления предела
. Результатом вычисления предела ![]() является производная функция
является производная функция ![]() .
.
Исходя из вышесказанного, сформулируем условия двух типовых задач:
– Найти производную в точке, используя определение производной.
– Найти производную функцию, используя определение производной. Эта версия, по моим наблюдениям, встречается заметно чаще и ей будет уделено основное внимание.
Принципиальное отличие заданий состоит в том, что в первом случае требуется найти число (как вариант, бесконечность), а во втором – функцию. Кроме того, производной может и вовсе не существовать.
Как найти производную по определению?
Составить отношение ![]() и вычислить предел
и вычислить предел ![]() .
.
Откуда появилась таблица производных и правила дифференцирования? Благодаря единственному пределу ![]() . Кажется волшебством, но в действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных, оттачивая алгоритм и технические приёмы решения:
. Кажется волшебством, но в действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных, оттачивая алгоритм и технические приёмы решения:
Пример 1
Найти производную функции ![]() , пользуясь определением производной
, пользуясь определением производной
По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице: ![]() .
.
Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую (конкретную) точку ![]() , принадлежащую области определения функции
, принадлежащую области определения функции ![]() , в которой существует производная. Зададим в данной точке приращение
, в которой существует производная. Зададим в данной точке приращение ![]() (разумеется, не выходящее за рамки о/о-я) и составим соответствующее приращение функции:
(разумеется, не выходящее за рамки о/о-я) и составим соответствующее приращение функции:
![]()
Вычислим предел:
![]()
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим числитель и знаменатель на сопряженное выражение ![]() :
:
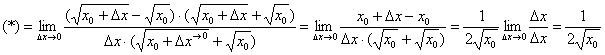
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций.
Итак, ![]() .
.
Поскольку в качестве ![]() можно выбрать ЛЮБУЮ точку
можно выбрать ЛЮБУЮ точку ![]() интервала
интервала ![]() , то, осуществив замену
, то, осуществив замену ![]() , получаем:
, получаем:
![]()
Ответ: по определению производной: ![]()
Готово.
В который раз порадуемся логарифмам:
Пример 2
Найти производную функции ![]() , пользуясь определением производной
, пользуясь определением производной
Решение: рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от подстрочного индекса и вместо буквы ![]() использовать букву
использовать букву ![]() .
.
Рассмотрим произвольную точку ![]() , принадлежащую области определения функции
, принадлежащую области определения функции ![]() (интервалу
(интервалу ![]() ), и зададим в ней приращение
), и зададим в ней приращение ![]() . А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
. А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
![]()
Найдём производную:
![]()
Простота оформления уравновешивается путаницей, которая может возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: ![]() – античная статуя, а
– античная статуя, а ![]() – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
– живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости ![]() закомментирую пошагово:
закомментирую пошагово:
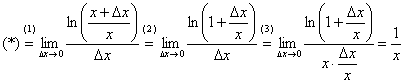
(1) Используем свойство логарифма ![]() .
.
(2) В скобках почленно делим числитель на знаменатель.
(3) В знаменателе искусственно домножаем и делим на «икс» чтобы воспользоваться замечательным пределом ![]() , при этом в качестве бесконечно малой величины выступает
, при этом в качестве бесконечно малой величины выступает ![]() .
.
Ответ: по определению производной: ![]()
Или конкретнее: ![]()
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Пример 3
Найти производную ![]() по определению
по определению
В данном случае составленное приращение ![]() сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
Пример 4
Найти производную ![]() по определению
по определению
А тут всё нужно свести к замечательному пределу ![]() . Решение оформлено вторым способом.
. Решение оформлено вторым способом.
Аналогично выводится ряд других табличных производных. Полный список можно найти в школьном учебнике, или, например, 1-м томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены формулой ![]() .
.
Продолжаем разбирать реальные практические задания:
Пример 5
Найти производную функции ![]() , используя определение производной
, используя определение производной
Решение: используем первый стиль оформления. Рассмотрим некоторую точку ![]() , принадлежащую
, принадлежащую ![]() (множеству действительных чисел), и зададим в ней приращение аргумента
(множеству действительных чисел), и зададим в ней приращение аргумента ![]() . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции:
![]()
Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение ![]() . Берём точку
. Берём точку ![]() (число) и находим в ней значение функции:
(число) и находим в ней значение функции: ![]() , то есть в функцию
, то есть в функцию ![]() вместо «икса» следует подставить
вместо «икса» следует подставить ![]() . Теперь берём тоже вполне конкретное число
. Теперь берём тоже вполне конкретное число ![]() и так же подставляем его в функцию
и так же подставляем его в функцию ![]() вместо «икса»:
вместо «икса»: ![]() . Записываем разность
. Записываем разность ![]() , при этом
, при этом ![]() нужно полностью взять в скобки.
нужно полностью взять в скобки.
Составленное приращение функции ![]() бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы ![]() , раскрываем скобки и уничтожаем противоположные члены::
, раскрываем скобки и уничтожаем противоположные члены::
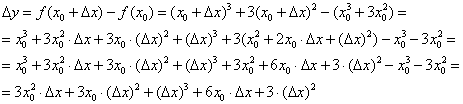
Индейка выпотрошена, с жаркое никаких проблем:
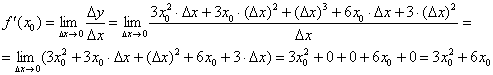
В итоге: ![]()
Поскольку в качестве ![]() можно выбрать любое действительное число, то проведём замену
можно выбрать любое действительное число, то проведём замену ![]() и получим
и получим ![]() .
.
Ответ: ![]() по определению.
по определению.
В целях проверки найдём производную с помощью правил дифференцирования и таблицы:
![]()
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Пример 6
Найти производную функции ![]() по определению производной
по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности:
![]()
Вернёмся к стилю № 2:
Пример 7
Пользуясь определением, найти производную функции
![]()
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции:
![]()
Решение: рассмотрим произвольную точку ![]() , принадлежащую
, принадлежащую ![]() , зададим в ней приращение аргумента
, зададим в ней приращение аргумента ![]() и составим приращение функции:
и составим приращение функции:
![]()
Найдём производную:
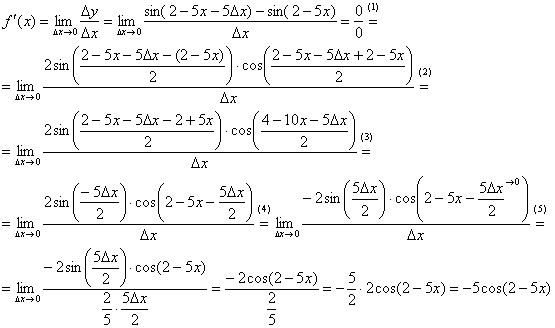
(1) Используем тригонометрическую формулу ![]() .
.
(2) Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3) Под синусом уничтожаем противоположные слагаемые, под косинусом почленно делим числитель на знаменатель.
(4) В силу нечётности синуса выносим «минус». Под косинусом указываем, что слагаемое ![]() .
.
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел ![]() . Таким образом, неопределённость устранена, причёсываем результат.
. Таким образом, неопределённость устранена, причёсываем результат.
Ответ: ![]() по определению
по определению
Как видите, основная трудность рассматриваемой задачи упирается в сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пример 8
Пользуясь определением, найти производную функции
![]()
Это задание для самостоятельного решения. Образец оформлен в том же духе, что предыдущий пример.
Разберём более редкую версию задачи:
Пример 9
Найти производную функции ![]() в точке
в точке ![]() , пользуясь определением производной.
, пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число
Проясним ответ стандартным способом:
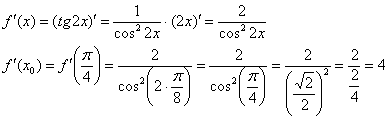
Решение: с точки зрения наглядности, это задание значительно проще, так как в формуле ![]() вместо
вместо ![]() рассматривается конкретное значение.
рассматривается конкретное значение.
Зададим в точке ![]() приращение
приращение ![]() и составим соответствующее приращение функции:
и составим соответствующее приращение функции:
![]()
Вычислим производную в точке:
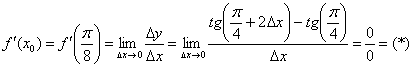
Используем весьма редкую формулу разности тангенсов ![]() и в который раз сведём решение к первому замечательному пределу:
и в который раз сведём решение к первому замечательному пределу:
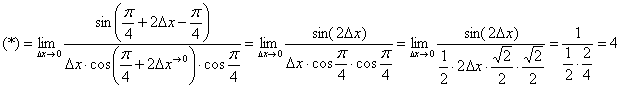
Ответ: ![]() по определению производной в точке.
по определению производной в точке.
Решение можно провести и в общем виде – для точки ![]() и уже в конце подставить
и уже в конце подставить ![]() .
.
Пример 10
Используя определение, найти производную функции ![]() в точке
в точке ![]()
Это пример для самостоятельного решения.
Заключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
Пример 11
Будет ли дифференцируема функция 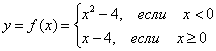 в точке
в точке ![]() ?
?
Решение: очевидно, что кусочно-заданная функция непрерывна в точке ![]() , но будет ли она там дифференцируема?
, но будет ли она там дифференцируема?
Алгоритм решения, причём не только для кусочных функций, таков:
1) Находим левостороннюю производную в данной точке: ![]() .
.
2) Находим правостороннюю производную в данной точке: ![]() .
.
3) Если односторонние производные конечны и совпадают: ![]() , то функция
, то функция ![]() дифференцируема в точке
дифференцируема в точке ![]() и геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной). Если получены два разных значения:
и геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной). Если получены два разных значения: ![]() (одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке
(одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке ![]() .
.
Если же обе односторонние производные равны бесконечности (пусть даже разных знаков), то функция ![]() не дифференцируема в точке
не дифференцируема в точке ![]() , но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).
, но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).
! Примечание: таким образом, между вопросами «Будет ли дифференцируема функция в точке?» и «Существует ли производная в точке?» есть разница!
Всё очень просто!
1) При нахождении левосторонней производной приращение аргумента отрицательно: ![]() , а слева от точки
, а слева от точки ![]() расположена парабола
расположена парабола ![]() , поэтому приращение функции равно:
, поэтому приращение функции равно:
![]()
И соответствующий левосторонний предел численно равен левосторонней производной в рассматриваемой точке:
![]()
2) Справа от точки ![]() находится график прямой
находится график прямой ![]() и приращение аргумента положительно:
и приращение аргумента положительно: ![]() . Таким образом, приращение функции:
. Таким образом, приращение функции:
![]()
Правосторонний предел и правосторонняя производная в точке:
![]()
3) Односторонние производные конечны и различны: ![]()
Ответ: функция не дифференцируема в точке ![]() .
.
Ещё легче доказывается книжный случай недифференцируемости модуля ![]() в точке
в точке ![]() , о котором я в общих чертах уже рассказал на теоретическом уроке о производной.
, о котором я в общих чертах уже рассказал на теоретическом уроке о производной.
Некоторые кусочно-заданные функции дифференцируемы и в точках «стыка» графика, например, котопёс 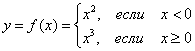 обладает общей производной и общей касательной (ось абсцисс) в точке
обладает общей производной и общей касательной (ось абсцисс) в точке ![]() . Кривой, да дифференцируемый на
. Кривой, да дифференцируемый на ![]() ! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
! Желающие могут убедиться в этом самостоятельно по образцу только что решённого примера.
На этом забавном гибриде и закончим повествование =)
Решения и ответы:
Пример 3. Решение: рассмотрим некоторую точку ![]() , принадлежащую области определения функции
, принадлежащую области определения функции ![]() . Зададим в данной точке приращение
. Зададим в данной точке приращение ![]() и составим соответствующее приращение функции:
и составим соответствующее приращение функции:
![]()
Найдём производную в точке ![]() :
:
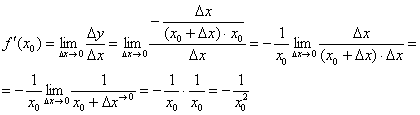
Так как в качестве ![]() можно выбрать любую точку
можно выбрать любую точку ![]() области определения функции
области определения функции ![]() , то
, то ![]() и
и ![]()
Ответ: ![]() по определению производной
по определению производной
Пример 4. Решение: рассмотрим произвольную точку ![]() , принадлежащую
, принадлежащую ![]() , и зададим в ней приращение
, и зададим в ней приращение ![]() . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции:
![]()
Найдём производную:
![]()
Используем замечательный предел ![]()
![]()
Ответ: ![]() по определению
по определению
Пример 6. Решение: рассмотрим некоторую точку ![]() , принадлежащую
, принадлежащую ![]() , и зададим в ней приращение аргумента
, и зададим в ней приращение аргумента ![]() . Тогда соответствующее приращение функции:
. Тогда соответствующее приращение функции:
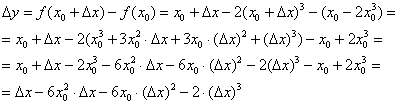
Вычислим производную:
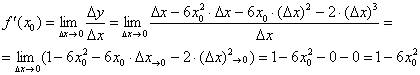
Таким образом: ![]()
Поскольку в качестве ![]() можно выбрать любое действительное число, то
можно выбрать любое действительное число, то ![]() и
и ![]()
Ответ: ![]() по определению.
по определению.
Пример 8. Решение: рассмотрим произвольную точку ![]() , принадлежащую
, принадлежащую ![]() , зададим в ней приращение
, зададим в ней приращение ![]() и составим приращение функции:
и составим приращение функции:
![]()
Найдём производную:
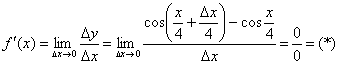
Используем тригонометрическую формулу ![]() и первый замечательный предел:
и первый замечательный предел:
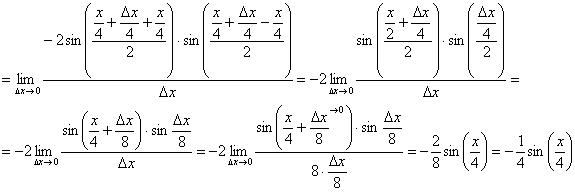
Ответ: ![]() по определению
по определению
Пример 10. Решение: зададим приращение ![]() в точке
в точке ![]() . Тогда приращение функции:
. Тогда приращение функции:
![]()
Вычислим производную в точке:
![]()
Умножим числитель и знаменатель на сопряженное выражение:
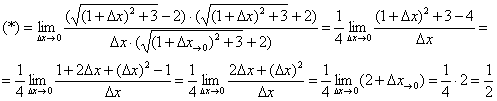
Ответ: ![]() по определению производной в точке
по определению производной в точке
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright