


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Частные производные функции трёх переменных
Продолжаем всеми любимую тему математического анализа – производные. В данной статье мы научимся находить частные производные функции трёх переменных: первые производные и вторые производные. Что необходимо знать и уметь для освоения материала? Не поверите, но, во-первых, нужно уметь находить «обычные» производные функции одной переменной – на высоком или хотя бы среднем уровне. Если с ними совсем туго, то начните с урока Как найти производную? Во-вторых, очень важно прочитать статью Частные производные функции двух переменных и осмыслить-прорешать если не все, то бОльшую часть примеров. Если это уже сделано, то уверенной походкой идём со мной, будет интересно, даже удовольствие получите!
Методы и принципы нахождения частных производных функции трёх переменных на самом деле очень похожи на частные производные функции двух переменных. Функция двух переменных, напоминаю, имеет вид ![]() , где «икс» и «игрек» – независимые переменные. Геометрически функция двух переменных обычно представляет собой некоторую поверхность в нашем трёхмерном пространстве.
, где «икс» и «игрек» – независимые переменные. Геометрически функция двух переменных обычно представляет собой некоторую поверхность в нашем трёхмерном пространстве.
Функция трёх переменных имеет вид ![]() , при этом переменные
, при этом переменные ![]() называются независимыми переменными или аргументами, переменная
называются независимыми переменными или аргументами, переменная ![]() называется зависимой переменной или функцией. Например:
называется зависимой переменной или функцией. Например: ![]() – функция трёх переменных
– функция трёх переменных
А теперь немного о фантастических фильмах и инопланетянах. Часто можно услышать о четырехмерном, пятимерном, десятимерном и т.д. пространствах. Чушь или нет?
Ведь функция трёх переменных ![]() подразумевает четырехмерное пространство
подразумевает четырехмерное пространство
(и действительно, переменных же три + сама функция). График функции трёх переменных представляет собой так называемую гиперповерхность. Представить её невозможно, поскольку мы живём в трехмерном пространстве (длина/ширина/высота). Чтобы вам со мной не было скучно, предлагаю викторину. Я задам несколько вопросов, а желающие могут попробовать на них ответить:
– Существует ли в мире четвертое, пятое и т.д. измерения в смысле обывательского понимания пространства (длина/ширина/высота)?
– Можно ли построить четырехмерное, пятимерное и т.д. пространство в широком понимании этого слова? То есть, привести пример такого пространства в нашей жизни.
– Возможно ли путешествие в прошлое?
– Возможно ли путешествие в будущее?
– Существуют ли инопланетяне?
На любой вопрос можно выбрать один из четырёх ответов:
Да / Нет (наукой это запрещено) / Наукой это не запрещено / Не знаю
Кто правильно ответит на все вопросы, тот, скорее всего, обладает некоторой вещью ;-)
Ответы на вопросы я постепенно буду выдавать по ходу урока, не пропускайте примеры!
Собственно, полетели. И сразу хорошая новость: для функции трёх переменных справедливы правила дифференцирования и таблица производных. Именно поэтому вам необходимо хорошо управляться с «обычными» производными функций одной переменной. Отличий совсем немного!
Пример 1
Найти частные производные первого порядка функции трёх переменных ![]()
Решение: Нетрудно догадаться – для функции трёх переменных существуют три частных производных первого порядка, которые обозначаются следующим образом:
![]() или
или ![]() – частная производная по «икс»;
– частная производная по «икс»;
![]() или
или ![]() – частная производная по «игрек»;
– частная производная по «игрек»;
![]() или
или ![]() – частная производная по «зет».
– частная производная по «зет».
В ходу больше обозначение со штрихом, но составители сборников, методичек в условиях задач очень любят использовать как раз громоздкие обозначения – так что не теряйтесь! Возможно, не все знают, как правильно читать вслух эти «страшные дроби». Пример: ![]() следует читать следующим образом: «дэ у по дэ икс».
следует читать следующим образом: «дэ у по дэ икс».
Начнём с производной по «икс»: ![]() . Когда мы находим частную производную по
. Когда мы находим частную производную по ![]() , то переменные
, то переменные ![]() и
и ![]() считаются константами (постоянными числами). А производная любой константы, о, благодать, равна нулю:
считаются константами (постоянными числами). А производная любой константы, о, благодать, равна нулю:
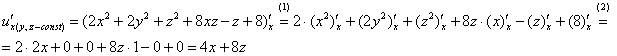
Сразу обратите внимание на подстрочный индекс ![]() – никто вам не запрещает помечать, что
– никто вам не запрещает помечать, что ![]() являются константами. Так даже удобнее, начинающим рекомендую использовать именно такую запись, меньше риск запутаться.
являются константами. Так даже удобнее, начинающим рекомендую использовать именно такую запись, меньше риск запутаться.
(1) Используем свойства линейности производной, в частности, выносим все константы за знак производной. Обратите внимание, что во втором слагаемом ![]() константу выносить не нужно: так как «игрек» является константой, то
константу выносить не нужно: так как «игрек» является константой, то ![]() – тоже константа. В слагаемом
– тоже константа. В слагаемом ![]() за знак производной вынесена «обычная» константа 8 и константа «зет».
за знак производной вынесена «обычная» константа 8 и константа «зет».
(2) Находим простейшие производные, не забывая при этом, что ![]() – константы. Далее причесываем ответ.
– константы. Далее причесываем ответ.
Частная производная ![]() . Когда мы находим частную производную по «игрек», то переменные
. Когда мы находим частную производную по «игрек», то переменные ![]() и
и ![]() считаются константами:
считаются константами:
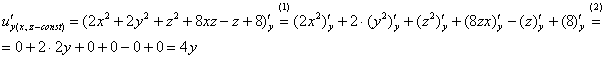
(1) Используем свойства линейности. И снова заметьте, что слагаемые ![]() ,
, ![]() являются константами, а значит, за знак производной выносить ничего не нужно.
являются константами, а значит, за знак производной выносить ничего не нужно.
(2) Находим производные, не забывая, что ![]() константы. Далее упрощаем ответ.
константы. Далее упрощаем ответ.
И, наконец, частная производная ![]() . Когда мы находим частную производную по «зет», то переменные
. Когда мы находим частную производную по «зет», то переменные ![]() и
и ![]() считаются константами:
считаются константами:
![]()
Общее правило очевидно и незатейливо: Когда мы находим частную производную по какой-либо независимой переменной, то две другие независимые переменные считаются константами.
При оформлении данных задач следует быть предельно внимательным, в частности, нельзя терять подстрочные индексы (которые указывают, по какой переменной проводится дифференцирование). Потеря индекса будет ГРУБЫМ НЕДОЧЁТОМ. Хммм…. забавно, если после такого устрашения я их сам где-нибудь пропущу)
Пример 2
Найти частные производные первого порядка функции трёх переменных ![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Рассмотренные два примера достаточно просты и, решив несколько подобных задачек, даже чайник приноровится расправляться с ними устно.
Для разгрузки вернемся к первому вопросу викторины: Существует ли в мире четвертое, пятое и т.д. измерения в смысле обывательского понимания пространства (длина/ширина/высота)?
Верный ответ: Наукой это не запрещено. Вся фундаментальная математическая аксиоматика, теоремы, математический аппарат прекрасно и непротиворечиво работают в пространстве любой размерности. Не исключено, что где-нибудь во Вселенной существуют неподвластные нашему разуму гиперповерхности, например, четырёхмерная гиперповерхность, которая задается функцией трех переменных ![]() . А может быть гиперповерхности рядом с нами или даже мы находимся прямо в них, просто наше зрение, другие органы чувств, сознание способны на восприятие и осмысление только трёх измерений.
. А может быть гиперповерхности рядом с нами или даже мы находимся прямо в них, просто наше зрение, другие органы чувств, сознание способны на восприятие и осмысление только трёх измерений.
Вернемся к примерам. Да, если кто сильно загрузился викториной, ответы на следующие вопросы лучше прочитать после того, как научитесь находить частные производные функции трёх переменных, а то я вам по ходу статьи вынесу весь мозг =)
Помимо простейших Примеров 1,2 на практике встречаются задания, которые можно назвать небольшой головоломкой. Такие примеры, к моей досаде, выпали из поля зрения, когда я создавал урок Частные производные функции двух переменных. Навёрстываем упущенное:
Пример 3
Найти частные производные первого порядка функции трёх переменных и составить полный дифференциал первого порядка
![]()
Решение: вроде бы тут «всё просто», но первое впечатление обманчиво. При нахождении частных производных многие будут гадать на кофейной гуще и ошибаться.
Разберём пример последовательно, чётко и понятно.
Начнём с частной производной по «икс». Когда мы находим частную производную по «икс», то переменные ![]() считаются константами. Следовательно, показатель нашей функции
считаются константами. Следовательно, показатель нашей функции ![]() – тоже константа. Для чайников рекомендую следующий приём решения: на черновике поменяйте константу
– тоже константа. Для чайников рекомендую следующий приём решения: на черновике поменяйте константу ![]() на конкретное положительное целое число, например, на «пятерку». В результате получится функция одной переменной:
на конкретное положительное целое число, например, на «пятерку». В результате получится функция одной переменной:
![]() или ещё можно записать так:
или ещё можно записать так: ![]()
Это степенная функция со сложным основанием (синусом). По правилу дифференцирования сложной функции:
![]()
Теперь вспоминаем, что ![]() , таким образом:
, таким образом:
![]()
На чистовике, конечно, решение следует оформить так:
![]()
Находим частную производную по «игрек», ![]() считаются константами. Если «икс» константа, то
считаются константами. Если «икс» константа, то ![]() – тоже константа. На черновике проделываем тот же трюк:
– тоже константа. На черновике проделываем тот же трюк: ![]() заменим, например, на 3, «зет» – заменим той же «пятёркой». В результате снова получается функция одной переменной:
заменим, например, на 3, «зет» – заменим той же «пятёркой». В результате снова получается функция одной переменной:
![]()
Это показательная функция со сложным показателем. По правилу дифференцирования сложной функции:
![]()
Теперь вспоминаем нашу замену: ![]()
Таким образом: ![]()
На чистовике, понятно, оформление должно выглядеть, благообразно:
![]()
И зеркальный случай с частной производной по «зет» (![]() – константы):
– константы):
![]()
При определенном опыте проведенный анализ можно проводить мысленно.
Выполняем вторую часть задания – составим дифференциал первого порядка. Это очень просто, по аналогии с функцией двух переменных, дифференциал первого порядка записывается по формуле:
![]()
В данном случае:
![]()
И делов то. Отмечу, что в практических задачах полный дифференциал 1-го порядка функции трёх переменных требуют составить значительно реже, чем для функции двух переменных.
Забавный пример для самостоятельного решения:
Пример 4
Найти частные производные первого порядка функции трёх переменных и составить полный дифференциал первого порядка
![]()
Полное решение и ответ в конце урока. Если возникнут затруднения, используйте рассмотренный «чайниковский» алгоритм, он гарантированно должен помочь. И ещё полезный совет – не спешите. Такие примеры быстро не решаю даже я.
Отвлекаемся и разбираем второй вопрос: Можно ли построить четырехмерное, пятимерное и т.д. пространство в широком понимании этого слова? То есть, привести пример такого пространства в нашей жизни.
Верный ответ: Да. Причём, очень легко. Например, добавляем к длине/ширине/высоте четвёртое измерение – время. Популярное четырехмерное пространство-время и всем известная теория относительности, аккуратно скомпилированная Эйнштейном по материалам трудов Лобачевского, Пуанкаре, Лоренца и Минковского. Тоже не все знают. За что у него Нобелевская премия? В научном мире был нешуточный скандал, и Нобелевский комитет сформулировал заслугу троечника Эйнштейна примерно следующим образом: «За общий вклад в развитие физики». Дальнейшее, что называется, раскрутка и пиар.
К рассмотренному четырехмерному пространству легко добавить пятое измерение, например: атмосферное давление. И так далее, так далее, так далее, сколько зададите измерений в своей модели – столько и будет. В широком смысле слова мы живём в многомерном пространстве.
Разберём еще пару типовых задач:
Пример 5
Найти частные производные первого порядка в точке ![]()
![]()
Решение: Задание в такой формулировке часто встречается на практике и предполагает выполнение следующих двух действий:
– нужно найти частные производные первого порядка;
– нужно вычислить значения частных производных 1-го порядка в точке ![]() .
.
Решаем:
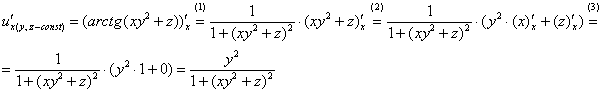
(1) Перед нами сложная функция, и на первом шаге следует взять производную от арктангенса. При этом мы, по сути, невозмутимо используем табличную формулу производной арктангенса ![]() . По правилу дифференцирования сложной функции результат необходимо домножить на производную внутренней функции (вложения):
. По правилу дифференцирования сложной функции результат необходимо домножить на производную внутренней функции (вложения): ![]() .
.
(2) Используем свойства линейности.
(3) И берём оставшиеся производные, не забывая, что ![]() – константы.
– константы.
По условию задания необходимо найти значение найденной частной производной ![]() в точке
в точке ![]() . Подставим координаты точки
. Подставим координаты точки ![]() в найденную производную:
в найденную производную:
![]()
Преимуществом данного задания является тот факт, что другие частные производные находятся по очень похожей схеме:
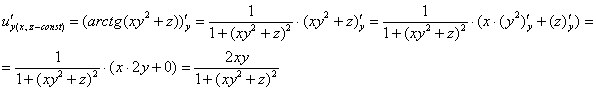
Как видите, шаблон решения практически такой же.
Вычислим значение найденной частной производной ![]() в точке
в точке ![]() :
:
![]()
И, наконец, производная по «зет»:
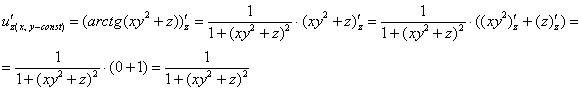
![]()
Готово. Решение можно было оформить и по другому: сначала найти все три частные производные, а потом вычислить их значения в точке ![]() . Но, мне кажется, приведенный способ удобнее – только нашли частную производную, и сразу, не отходя от кассы, вычислили её значение в точке.
. Но, мне кажется, приведенный способ удобнее – только нашли частную производную, и сразу, не отходя от кассы, вычислили её значение в точке.
Интересно отметить, что геометрически точка ![]() – вполне реальная точка нашего трехмерного пространства. Значения же функции
– вполне реальная точка нашего трехмерного пространства. Значения же функции ![]() , производных
, производных ![]() – уже четвертое измерение, и где оно геометрически находится, никто не знает. Как говорится, по Вселенной никто с рулеткой не ползал, не проверял.
– уже четвертое измерение, и где оно геометрически находится, никто не знает. Как говорится, по Вселенной никто с рулеткой не ползал, не проверял.
Коль скоро снова философская тема пошла, рассмотрим третий вопрос: Возможно ли путешествие в прошлое?
Верный ответ: Нет. Путешествие в прошлое противоречит второму закону термодинамики о необратимости физических процессов (энтропии). Так что не ныряйте, пожалуйста, в бассейн без воды, событие можно открутить назад только в видеозаписи =) Народная мудрость не зря придумала противоположный житейский закон: «Семь раз отмерь, один раз отрежь». Хотя, на самом деле грустная штука, время однонаправлено и необратимо, никто из нас завтра не помолодеет. А различные фантастические фильмы вроде «Терминатора» с научной точки зрения – полная чушь. Абсурд и с точки зрения философии – когда Следствие, вернувшись в прошлое, может уничтожить собственную же Причину.
Пример 6
Найти частные производные первого порядка в точке ![]()
![]()
Пример 7
Найти частные производные первого порядка в точке ![]()
![]()
Это два несложных примера для самостоятельного решения. Полное решение и ответ в конце урока.
Но вы не расстраивайтесь из-за второго закона термодинамики, сейчас я всех приободрю более сложными примерами:
Пример 8
Найти частные производные первого порядка функции трёх переменных
![]()
Решение: Найдем частные производные первого порядка:
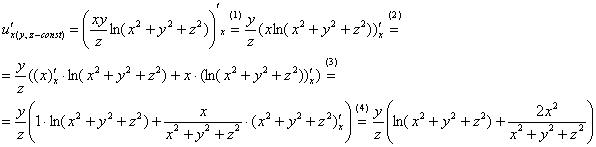
(1) Начиная находить производную, следует придерживаться того же подхода, что и для функции одной переменной. Используем свойства линейности, в данном случае выносим за знак производной константы ![]() .
.
(2) Под знаком производной у нас находится произведение двух функций, каждая из которых зависит от нашей «живой» переменной «икс». Поэтому необходимо использовать правило дифференцирования произведения ![]() .
.
(3) С производной ![]() сложностей никаких, а вот производная
сложностей никаких, а вот производная ![]() является производной сложной функции: сначала необходимо найти, по сути, табличный логарифм
является производной сложной функции: сначала необходимо найти, по сути, табличный логарифм ![]() и домножить его на производную от вложения.
и домножить его на производную от вложения.
(4) Думаю, все уже освоились с простейшими примерами вроде ![]() – тут у нас «живой» только
– тут у нас «живой» только ![]() , производная которого равна
, производная которого равна ![]()
Практически зеркален случай с производной по «игрек», его я запишу короче и без комментариев:
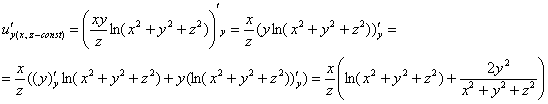
Интереснее с производной по «зет», хотя, всё равно почти то же самое:
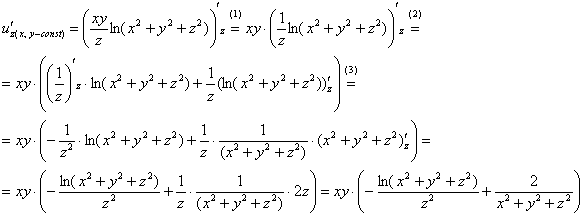
(1) Выносим константы за знак производной.
(2) Здесь опять произведение двух функций, каждая из которых зависит от «живой» переменной «зет». В принципе, можно использовать формулу производной частного, но проще таки пойти другим путём – найти производную от произведения.
(3) Производная 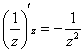 – это табличная производная. Во втором слагаемом – уже знакомая производная сложной функции.
– это табличная производная. Во втором слагаемом – уже знакомая производная сложной функции.
Готово.
Пример 9
Найти частные производные первого порядка функции трёх переменных
![]()
Это пример для самостоятельного решения. Подумайте, как рациональнее находить ту или иную частную производную. Полное решение и ответ в конце урока.
Перед тем как перейти к заключительным примерам урока и рассмотреть частные производные второго порядка функции трёх переменных, всех еще раз взбодрю четвертым вопросом:
Возможно ли путешествие в будущее?
Верный ответ: Наукой это не запрещено. Парадоксально, но не существует математического, физического, химического или другого естественнонаучного закона, который бы запрещал путешествие в будущее! Кажется чушью? Но практически у каждого в жизни бывало предчувствие (причём, не подкрепленное никакими логическими доводами), что произойдет то или иное событие. И оно происходило! Откуда пришла информация? Из будущего? Таким образом, фантастические фильмы о путешествии в будущее, да и, к слову, предсказания всевозможных гадалок, экстрасенсов нельзя назвать таким уж бредом. По крайне мере, наука этого не опровергла. Всё возможно! Так, когда я учился в школе, то компакт диски и плоские мониторы из фильмов казались мне невероятной фантастикой.
Известная комедия «Иван Васильевич меняет профессию» – выдумка наполовину (как максимум). Никакой научный закон не запрещал Ивану Грозному оказаться в будущем, но невозможно, чтобы два перца оказались в прошлом и исполняли обязанности царя.
Частные производные второго порядка функции трёх переменных
Общий принцип нахождения частных производных второго порядка функции трёх переменных аналогичен принципу нахождения частных производных 2-го порядка функции двух переменных. Поэтому, если вы хорошо проработали урок Частные производные функции двух переменных, то будет всё очень просто.
Для того чтобы найти частные производные второго порядка, сначала необходимо найти частные производные первого порядка ![]() или в другой записи:
или в другой записи: ![]() .
.
Частных производных второго порядка девять штук.
Первая группа – это вторые производные по тем же переменным:
![]() или
или ![]() – вторая производная по «икс»;
– вторая производная по «икс»;
![]() или
или ![]() – вторая производная по «игрек»;
– вторая производная по «игрек»;
![]() или
или ![]() – вторая производная по «зет».
– вторая производная по «зет».
Вторая группа – это смешанные частные производные 2-го порядка, их шесть:
![]() или
или ![]() – смешанная производная «икс по игрек»;
– смешанная производная «икс по игрек»;
![]() или
или ![]() – смешанная производная «игрек по икс»;
– смешанная производная «игрек по икс»;
![]() или
или ![]() – смешанная производная «икс по зет»;
– смешанная производная «икс по зет»;
![]() или
или ![]() – смешанная производная «зет по икс»;
– смешанная производная «зет по икс»;
![]() или
или ![]() – смешанная производная «игрек по зет»;
– смешанная производная «игрек по зет»;
![]() или
или ![]() – смешанная производная «зет по игрек».
– смешанная производная «зет по игрек».
Как и для случая функции двух переменных, при решении задач можно ориентироваться на следующие равенства смешанных производных второго порядка:
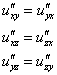
Примечание: строго говоря, это не всегда так
На всякий случай несколько примеров, как правильно читать сиё безобразие вслух:
![]() – «у два штриха дважды по игрек»;
– «у два штриха дважды по игрек»;
![]() – «дэ два у по дэ зет квадрат»;
– «дэ два у по дэ зет квадрат»;
![]() – «у два штриха по икс по зет»;
– «у два штриха по икс по зет»;
![]() – «дэ два у по дэ зет по дэ игрек».
– «дэ два у по дэ зет по дэ игрек».
Примеры на нахождение частных производных 2-го прядка для функции трёх переменных на практике встречаются реже. Обычно они не очень сложные, но довольно большие по объему.
Пример 10
Найти все частные производные первого и второго порядка функции трёх переменных
![]()
Записать полный дифференциал 2-го порядка – вы его хотели, и вы его получили! :)
Решение: сначала найдем частные производные первого порядка:
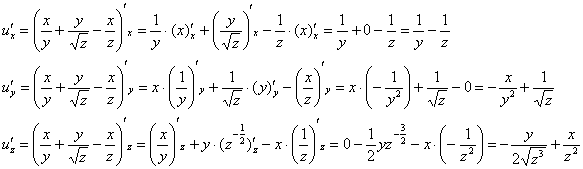
Частные производные второго порядка рекомендую начинать искать со смешанных производных, поскольку это позволит выяснить, а правильно ли вообще найдены производные первого порядка.
Берём найденную производную ![]() и дифференцируем её по «игрек»:
и дифференцируем её по «игрек»:
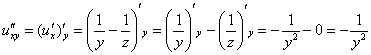
Берём найденную производную ![]() и дифференцируем её по «икс»:
и дифференцируем её по «икс»:
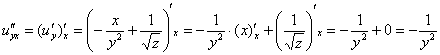
Равенство ![]() выполнено. Гуд.
выполнено. Гуд.
Разбираемся со второй парой смешанных производных.
Берём найденную производную ![]() и дифференцируем её по «зет»:
и дифференцируем её по «зет»:
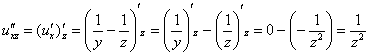
Берём найденную производную ![]() и дифференцируем её по «икс»:
и дифференцируем её по «икс»:
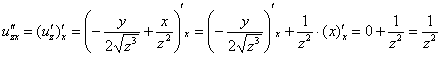
![]() – всё путём.
– всё путём.
Аналогично разбираемся с третьей парой смешанных производных:
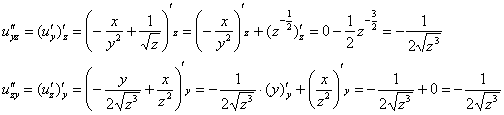
![]() Нормалёк.
Нормалёк.
После проделанных трудов гарантированно можно утверждать, что, во-первых, мы правильно нашли все частные производные 1-го порядка, во-вторых, правильно нашли и смешанные частные производные 2-го порядка.
Осталось найти ещё три частные производные второго порядка, вот здесь уже во избежание ошибок следует максимально сконцентрировать внимание:
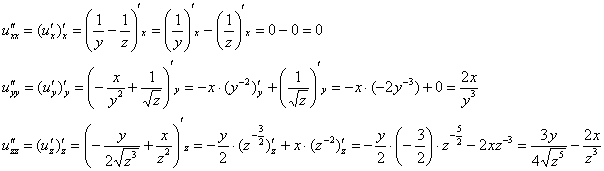
И по горячим пожеланиям землян, составим полный дифференциал второго порядка:
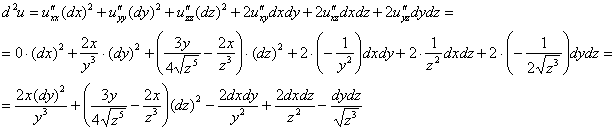
Готово. Повторюсь, задание не столько сложное, сколько объемное. Решение можно сократить и сослаться на равенства смешанных частных производных, но в этом случае не будет проверки. Поэтому лучше таки потратить время и найти все производные (к тому же это может потребовать преподаватель), или, в крайнем случае, выполнить проверку на черновике.
Пример 11
Найти все частные производные первого и второго порядка функции трёх переменных
![]()
Это пример для самостоятельного решения. Краткое решение и ответ в конце урока, который подошел к финальному вопросу:
– Существуют ли инопланетяне?
Верный ответ: Не знаю. Было бы странным, если бы вы ответили «да» или «нет». С одной стороны, откуда вы знаете, что их нет? С другой стороны, даже если вы видели гуманоидов и лично с ними общались, то ответ «да» прозвучит ещё страннее =)
Кто правильно ответил на все 5 вопросов, тот, скорее всего, обладает дипломом ФМ или другого естественно-технического факультета.
Ну а мне пора садиться в летающую тарелку и возвращаться к себе домой в Туманность Андромеды.
Ку.
Решения и ответы:
Пример 2: Решение:
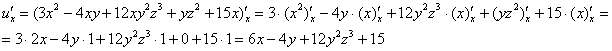
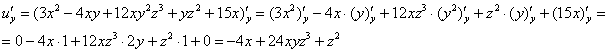
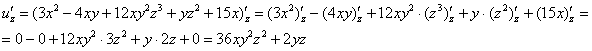
Пример 4: Решение: Найдем частные производные первого порядка.
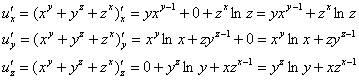
Составим полный дифференциал первого порядка:
![]()
Пример 6: Решение: Вычислим частные производные первого порядка в точке ![]() :
:

Пример 7: Решение: Вычислим частные производные первого порядка в точке ![]() :
:
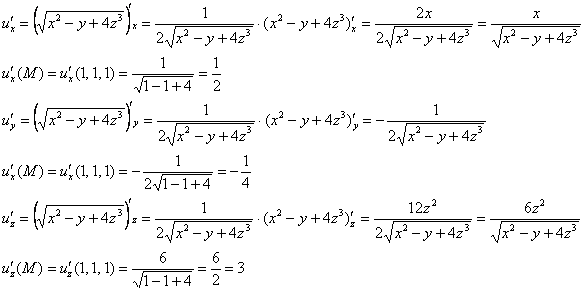
Пример 9: Решение: Найдем частные производные первого порядка:
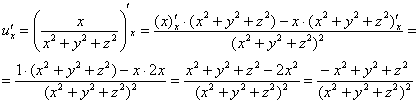

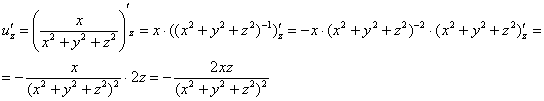
Пример 11: Решение: Найдем частные производные первого порядка:
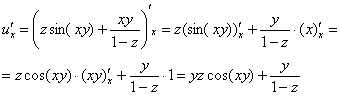
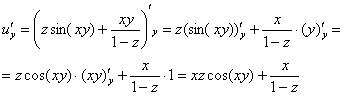
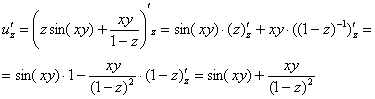
Найдем частные производные второго порядка:
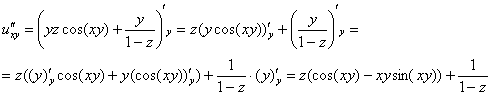
![]()
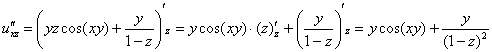
![]()
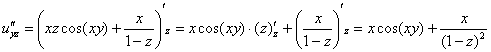
![]()
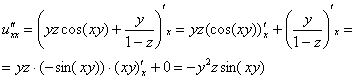
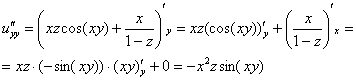
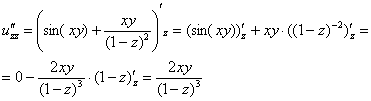
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright