


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Зависимость и коэффициент ковариации
непрерывных случайных величин
На предыдущем уроке мы рассмотрели функции распределения и плотности непрерывной двумерной случайной величины и в заключительной статье разбёрём: зависимость и независимость этой СВ, условные законы распределения, матожидания, коэффициент ковариации и корреляции. Коротко теория, подробно задачи.
И сразу быстренько вспоминаем: две случайные величины являются независимыми, если закон распределения одной из них не зависит от того, какое значение значения приняла другая случайная величина. Например, случайные погрешности измерений ![]() двух независимо работающих измерительных приборов.
двух независимо работающих измерительных приборов.
Если же СВ зависимы, то закон распределения одной величины зависит от того, какое значение приняла другая величина. Классика жанра: ![]() – рост случайно выбранного человека,
– рост случайно выбранного человека, ![]() – его вес. Ну, или наоборот, сначала смотрим на вес, а затем анализируем закон распределения роста.
– его вес. Ну, или наоборот, сначала смотрим на вес, а затем анализируем закон распределения роста.
Условные законы распределения случайных величин обозначаются следующим образом:
![]() – условный закон распределения СВ
– условный закон распределения СВ ![]() , при условии, что СВ
, при условии, что СВ ![]() примет (или уже приняла) какое-либо КОНКРЕТНОЕ значение
примет (или уже приняла) какое-либо КОНКРЕТНОЕ значение ![]() :
:
![]() – условный закон распределения
– условный закон распределения ![]() , при условии, что
, при условии, что ![]() примет или уже приняла некоторое КОНКРЕТНОЕ значение
примет или уже приняла некоторое КОНКРЕТНОЕ значение ![]() .
.
В случае независимости случайных величин все условные законы ![]() будут совпадать с законом распределения случайной величины
будут совпадать с законом распределения случайной величины ![]() (ибо «игрековая» величина никак не влияет на «иксовую»), и все условные законы
(ибо «игрековая» величина никак не влияет на «иксовую»), и все условные законы ![]() – совпадать с законом
– совпадать с законом ![]() .
.
Но вот с зависимыми величинами всё не так: встретился нам мальчик-с-пальчик ![]() , и мы сталкиваемся с
, и мы сталкиваемся с ![]() – условным законом распределения веса именно этой «ростовой категории». А вот если попался дядя Стёпа, то условный закон распределения веса
– условным законом распределения веса именно этой «ростовой категории». А вот если попался дядя Стёпа, то условный закон распределения веса ![]() таких дядей стёп будет совсем другим.
таких дядей стёп будет совсем другим.
С нахождением условных законов дискретных СВ мы уже разобрались (см. по ссылке), и сейчас научимся их строить для непрерывных случайных величин:
Пример 9
Двумерная непрерывная случайная величина ![]() задана своей плотностью распределения
задана своей плотностью распределения ![]() в квадрате
в квадрате ![]() и принимает значения только из этой области. Найти:
и принимает значения только из этой области. Найти:
1) ![]() – плотности распределения компонент
– плотности распределения компонент ![]() и их матожидания
и их матожидания ![]() ;
;
2) Условные плотности ![]() и условные математические ожидания
и условные математические ожидания ![]()
Сделать вывод о зависимости или независимости случайных величин.
Решение: функцию плотности ![]() я взял из Примера 8 и первый пункт решения уже частично готов:
я взял из Примера 8 и первый пункт решения уже частично готов:
1) а именно, найдены функции ![]() :
:
![]()
Для удобства я воспользуюсь тригонометрической формулой ![]() и перепишу функцию в виде:
и перепишу функцию в виде:
![]()
Аналогично:
![]()
Напомню смысл этих функций. Функция ![]() задаёт закон распределения случайной величины
задаёт закон распределения случайной величины ![]() без учёта возможного влияния на него случайной величины
без учёта возможного влияния на него случайной величины ![]() (эта оговорка нужна на тот случай, если
(эта оговорка нужна на тот случай, если ![]() зависимы). И «зеркально»: функция
зависимы). И «зеркально»: функция ![]() определяет закон распределения СВ
определяет закон распределения СВ ![]() – без учёта возможного влияния СВ
– без учёта возможного влияния СВ![]() .
.
По этой причине функции ![]() иногда называют безусловными плотностями распределения компонент
иногда называют безусловными плотностями распределения компонент ![]() , и сейчас нам нужно вычислить их безусловные математические ожидания
, и сейчас нам нужно вычислить их безусловные математические ожидания ![]() .
.
По формуле математического ожидания:
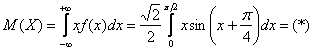
Используем формулу интегрирования по частям в определённом интеграле:

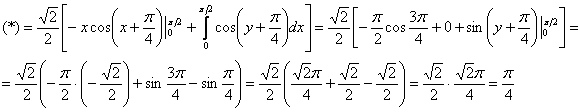
Так как плотности компонент совпадают, то работы у нас в два раза меньше:
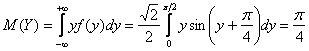
2) Найдём плотность распределения ![]() случайной величины
случайной величины ![]() при условии, что случайная величина
при условии, что случайная величина ![]() принимает различные КОНКРЕТНЫЕ значения
принимает различные КОНКРЕТНЫЕ значения ![]() . Эта функция принципиально отличатся от
. Эта функция принципиально отличатся от ![]() тем, что учитывает влияние
тем, что учитывает влияние ![]() (если оно есть), и поэтому её называют условной плотностью распределения случайной величины
(если оно есть), и поэтому её называют условной плотностью распределения случайной величины ![]() .
.
Данная функция определяется по формуле:
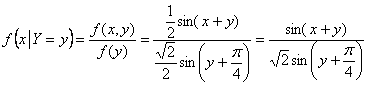
Легко видеть, что закон распределения случайной величины ![]() зависит от того, какое значение приняла переменная
зависит от того, какое значение приняла переменная ![]() . Так, например, при
. Так, например, при ![]() получаем:
получаем:
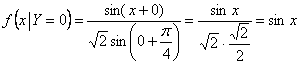 , если
, если ![]() и
и ![]() при иных значениях
при иных значениях ![]() .
.
А если, например, ![]() , то получается совсем другая плотность:
, то получается совсем другая плотность:
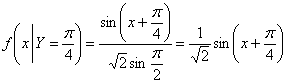 – на том же промежутке
– на том же промежутке ![]() .
.
Задание: самостоятельно проверьте, что любая из полученных функций обладает общими свойствами функции плотности: ![]() и
и ![]() .
.
Таким образом, здесь можно сразу сделать вывод о том, что двумерная случайная величина ![]() состоит из зависимых компонент.
состоит из зависимых компонент.
По «зеркальной» формуле получаем:
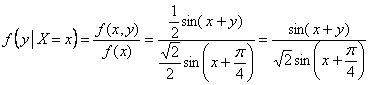 – условную плотность распределения случайной величины
– условную плотность распределения случайной величины ![]() , при условии, что случайная величина
, при условии, что случайная величина ![]() принимает различные КОНКРЕТНЫЕ значения
принимает различные КОНКРЕТНЫЕ значения ![]() из промежутка
из промежутка ![]() .
.
Условные математические ожидания рассчитываются по формулам:
![]()
и для разнообразия я вычислю условное «игрековое» матожидание:
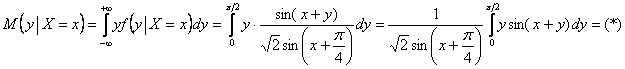
Снова интегрируем по частям, и тут главное не запутаться в буквах: «икс» считается константой, а «игрек» – «живая» переменная:
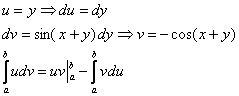
по ходу дальнейших преобразований используем формулы приведения:

Найденное математическое ожидание:
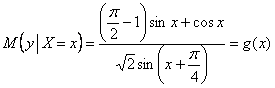 – представляет собой функцию, зависящую от
– представляет собой функцию, зависящую от ![]() , и называется функцией регрессии
, и называется функцией регрессии ![]() на
на ![]() . И это естественно – если «икс» принимает различные значения, то мы получаем разные условные законы распределения с разными матожиданиями. Так, при
. И это естественно – если «икс» принимает различные значения, то мы получаем разные условные законы распределения с разными матожиданиями. Так, при ![]() получается следующий условный закон распределения:
получается следующий условный закон распределения:
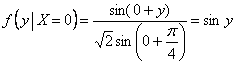 и с помощью найденной функции легко рассчитать соответствующее математическое ожидание:
и с помощью найденной функции легко рассчитать соответствующее математическое ожидание:
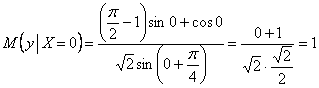
Желающие могут выполнить проверку непосредственным вычислением интеграла 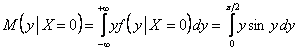
И особо желающие (такие есть!) могут самостоятельно провести аналогичные вычисления, чтобы получить:
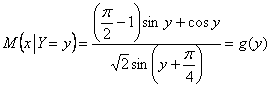 – условное математическое ожидание компоненты
– условное математическое ожидание компоненты ![]() , которое называется функцией регрессии
, которое называется функцией регрессии ![]() на
на ![]() .
.
Следует заметить, что в отличие от уравнения, которое мы получаем с помощью коэффициента корреляции (также см. ниже), регрессия здесь носит в общем случае нелинейный характер.
Вывод о зависимости случайных величин ![]() уже сделан, и решение этой задачи завершено.
уже сделан, и решение этой задачи завершено.
Существуют ли другие способы определения зависимости / независимости? Существуют!
Теорема: для того, чтобы случайные величины ![]() были независимыми, необходимо и достаточно, чтобы функция распределения системы
были независимыми, необходимо и достаточно, чтобы функция распределения системы ![]() была равна произведению функций распределения составляющих:
была равна произведению функций распределения составляющих:
![]()
и, как следствие, аналогичное утверждение справедливо для плотностей:
![]()
И если случайные величины независимы, то закон распределения любой из них действительно не зависит от того, какое значение приняла другая величина:
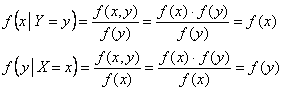
Иными словами, любое условное распределение той или иной компоненты равно соответствующему безусловному распределению.
Творческое задание для самостоятельного решения:
Пример 10
Двумерная непрерывная случайная величина ![]() задана своей плотностью распределения
задана своей плотностью распределения ![]() в области
в области ![]() и может принимать значения только из этой полосы.
и может принимать значения только из этой полосы.
1) Найти плотности распределения ![]() составляющих
составляющих ![]() сделать вывод о зависимости / независимости этих случайных величин.
сделать вывод о зависимости / независимости этих случайных величин.
Эти функции можно найти методом подбора (уроки о равномерном и нормальном распределении в помощь), но надёжнее использовать общие формулы ![]() ,
, ![]() (см. Пример 6). Справочно:
(см. Пример 6). Справочно: 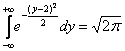 (частный случай интеграла Гаусса – см. урок о нормальном распределении).
(частный случай интеграла Гаусса – см. урок о нормальном распределении).
2) Вычислить ![]()
Здесь нужно использовать свойства матожидания и дисперсии (см. Пример 2 первого урока о системах случайных величин). И небольшая подсказка: для нахождения ![]() удобно использовать формулу вычисления дисперсии
удобно использовать формулу вычисления дисперсии ![]() , и для
, и для ![]() – ту же формулу, запишу её в общем виде:
– ту же формулу, запишу её в общем виде: ![]() .
.
Краткое решение в конце урока.
Следует отметить, что озвученная выше теорема с простенькими формулами ![]() ,
, ![]() часто порождает одно практическое заблуждение. Так, в Примере 6 мы отыскали функцию распределения
часто порождает одно практическое заблуждение. Так, в Примере 6 мы отыскали функцию распределения ![]() и видим, что в ней можно разделить «икс» и «игрек», т.е. всё вроде бы хорошо и функция представима в виде
и видим, что в ней можно разделить «икс» и «игрек», т.е. всё вроде бы хорошо и функция представима в виде ![]() . Однако этот «критерий» ошибочен! Ведь мы НЕ ЗНАЕМ функций
. Однако этот «критерий» ошибочен! Ведь мы НЕ ЗНАЕМ функций ![]() . В общем случае, они могут оказаться какими угодно и совершенно неожиданными – такими, что их произведение
. В общем случае, они могут оказаться какими угодно и совершенно неожиданными – такими, что их произведение ![]() вовсе не равно
вовсе не равно ![]() !
!
Поэтому нужно обязательно найти ![]() , выполнить умножение
, выполнить умножение ![]() и только после этого делать вывод о справедливости равенства
и только после этого делать вывод о справедливости равенства ![]() и независимости случайных величин!
и независимости случайных величин!
Иными словами, если у функций ![]() ,
, ![]() можно разделить аргументы, то это ЕЩЁ НЕ ЗНАЧИТ, что справедливы равенства
можно разделить аргументы, то это ЕЩЁ НЕ ЗНАЧИТ, что справедливы равенства ![]() ,
, ![]()
Любопытно, что в «неразделимом» случае это рассуждение срабатывает. Так, у функции плотности ![]() (Пример 8-9) «икс» с «игреком» разделить нельзя, и из этого следует, что она никак не может получиться в результате перемножения функций
(Пример 8-9) «икс» с «игреком» разделить нельзя, и из этого следует, что она никак не может получиться в результате перемножения функций ![]() , следовательно, компоненты
, следовательно, компоненты ![]() зависимы.
зависимы.
Но такое обоснование всё же не убедительно – а вдруг, если «покрутить-повертеть» ![]() , использовать тригонометрические формулы, то переменные таки разделятся? Поэтому надежнее отыскать условные плотности
, использовать тригонометрические формулы, то переменные таки разделятся? Поэтому надежнее отыскать условные плотности![]() ,
, ![]() , их произведение:
, их произведение:
![]()
и только после этого делать вывод, что ![]()
Эта тонкость встретится и в заключительном задании, где мы рассмотрим коэффициенты ковариации и корреляции. Их смысл я уже осветил на уроке о зависимых дискретных СВ, и сейчас мы изучим техническую сторону вопроса для непрерывных СВ:
Пример 11
Задана плотность распределения системы двух случайных величин
![]()
Найти значение ![]() и вычислить коэффициенты ковариации
и вычислить коэффициенты ковариации ![]() и корреляции
и корреляции ![]() . Построить уравнение линейной регрессии
. Построить уравнение линейной регрессии ![]() на
на ![]() .
.
И, во-первых, сразу заметим, что аргументы функции плотности здесь разделяются. Но из этого вовсе не следует справедливость равенства ![]() и независимость компонент
и независимость компонент ![]() . Этот момент у нас прояснится только в ходе решения:
. Этот момент у нас прояснится только в ходе решения:
1) Константу ![]() найдём из свойства функции плотности двумерной СВ:
найдём из свойства функции плотности двумерной СВ:
![]()
Так как случайная величина принимает значения лишь из ограниченной области ![]() , то свойство упрощается до двойного интеграла по этой области:
, то свойство упрощается до двойного интеграла по этой области: ![]() , в данном случае:
, в данном случае:
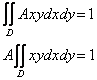
И нам предстоит решить шаблонную задачу. Представим уравнение прямой в «школьном» виде: ![]() , изобразим область интегрирования на чертеже:
, изобразим область интегрирования на чертеже:
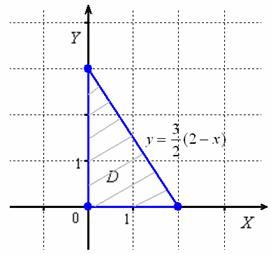
и выберем традиционный порядок обхода области:
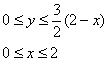
Таким образом: 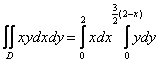 . С двойным интегралом удобно разделаться поэтапно, у кого возникнут трудности с техникой вычислений, обратитесь по ссылке выше:
. С двойным интегралом удобно разделаться поэтапно, у кого возникнут трудности с техникой вычислений, обратитесь по ссылке выше:
1) 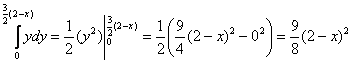
2) 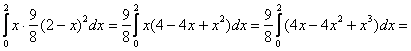
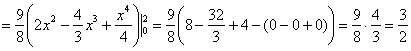
И из равенства ![]() получаем:
получаем:
![]()
Итак: 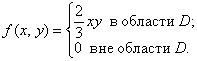
Коэффициенты ковариации и корреляции определяются по тем же формулам:
![]() – с той поправкой, что матожидания и стандартные отклонения рассчитываются с помощью интегралов.
– с той поправкой, что матожидания и стандартные отклонения рассчитываются с помощью интегралов.
Математическое ожидание произведения СВ вычислим по формуле:
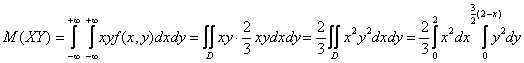
1) 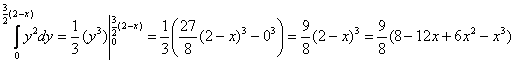
2) 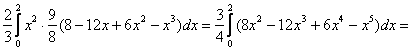
![]()
Математические ожидания компонент ![]() тоже можно вычислить с помощью двойных интегралов:
тоже можно вычислить с помощью двойных интегралов:
![]() , в данном случае это будут двойные интегралы по области
, в данном случае это будут двойные интегралы по области ![]() , либо с помощью однократных интегралов от безусловных плотностей этих случайных величин:
, либо с помощью однократных интегралов от безусловных плотностей этих случайных величин:
![]()
То же самое касается дисперсий:
![]() , либо:
, либо:
![]()
В исследовательских целях выберем 2-й способ, который, кстати, не легче.
Сначала разделаемся с компонентой ![]() . Найдём её безусловную плотность:
. Найдём её безусловную плотность:
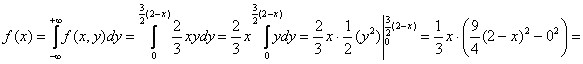
![]() и
и ![]() при иных значениях
при иных значениях ![]() .
.
Для самоконтроля обязательно проверяем, что ![]() , я выполнил эту проверку на черновике.
, я выполнил эту проверку на черновике.
Вычислим математическое ожидание:
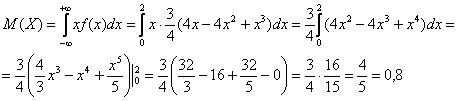
Дисперсию вычислим по формуле:
![]()
В данном случае:
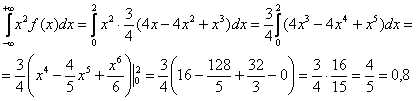
Таким образом:
![]()
и среднее квадратическое отклонение:
![]()
Теперь компонента ![]() . Чтобы составить её функцию плотности, нужно из уравнения прямой
. Чтобы составить её функцию плотности, нужно из уравнения прямой ![]() выразить
выразить ![]() и тогда «икс» у нас будет «заходить» в область
и тогда «икс» у нас будет «заходить» в область ![]() через ось ординат и «выходить» через прямую
через ось ординат и «выходить» через прямую ![]() :
:
 , а давайте-ка самостоятельно. Формулы вверху, образец для сверки – внизу, ну а здесь я сразу запишу готовые результаты:
, а давайте-ка самостоятельно. Формулы вверху, образец для сверки – внизу, ну а здесь я сразу запишу готовые результаты:
![]() , если
, если ![]() – и после нахождения этой функции, становится ясно, что при её умножении на
– и после нахождения этой функции, становится ясно, что при её умножении на ![]() у нас не получается
у нас не получается ![]() ! Таким образом,
! Таким образом, ![]() , а значит, случайные величины
, а значит, случайные величины ![]() – зависимы.
– зависимы.
Остальные трофеи: ![]()
И долгожданный коэффициент совместной вариации:
![]() – редкий, как солнечное затемнение, случай, когда вычисления было удобнее провести в десятичных дробях.
– редкий, как солнечное затемнение, случай, когда вычисления было удобнее провести в десятичных дробях.
Впрочем, это ненадолго:)
![]()
Коэффициент корреляции отрицателен и по модулю достаточно близок к единице – это означает, что между случайными величинами ![]() существует довольно тесная вероятностная линейная зависимость.
существует довольно тесная вероятностная линейная зависимость.
Уравнение линейной регрессии ![]() на
на ![]() строится по той же формуле, что и в дискретном случае:
строится по той же формуле, что и в дискретном случае:
![]() , где
, где ![]() ,
, ![]() .
.
Давно не встречал такой красоты:
![]() , вот что бывает после затмения :)
, вот что бывает после затмения :)
Полученное уравнение означает, что если случайная величина ![]() приняла какое-нибудь значение (из промежутка
приняла какое-нибудь значение (из промежутка ![]() ), например,
), например, ![]() , то мы можем быстро оценить наиболее вероятные значения, которые может принять случайная величина
, то мы можем быстро оценить наиболее вероятные значения, которые может принять случайная величина ![]() – эти значения находятся вблизи точки
– эти значения находятся вблизи точки ![]() . И поскольку коэффициент корреляции близок по модулю к единице, то полученное приближение будет достаточно точным.
. И поскольку коэффициент корреляции близок по модулю к единице, то полученное приближение будет достаточно точным.
Готово.
Как и в случае с дискретными СВ, для рассмотренных коэффициентов справедливы следующие факты:
Если в результате решения мы выяснили, что ![]() , то из этого следует, что случайные величины
, то из этого следует, что случайные величины ![]() являются зависимыми или коррелированными. Но если получен результат
являются зависимыми или коррелированными. Но если получен результат ![]() , то СВ могут оказаться как независимыми, так и зависимыми (т.к. зависимость может носить не только линейный характер); однако и в том и другом случае их называют некоррелированными.
, то СВ могут оказаться как независимыми, так и зависимыми (т.к. зависимость может носить не только линейный характер); однако и в том и другом случае их называют некоррелированными.
Из последнего утверждения существуют исключения, в частности, из некоррелированности компонент двумерной нормальной СВ следует и их независимость.
Теперь вас ничем не испугаешь :), и поэтому я запишу напоследок общую формулу плотности двумерной нормальной случайной величины:

…а это уже какая-то вспышка на Солнце.
В случае некоррелированности компонент ![]() получаем:
получаем:

и после финального преобразования чётко видно, что перед нами произведение нормальных плотностей случайных величин ![]() . Таким образом, равенство
. Таким образом, равенство ![]() справедливо и они независимы.
справедливо и они независимы.
Дополнительную информацию и примеры можно найти в учебном пособии (новые издания) и задачнике В.Е. Гмурмана, ну а мой практикум подошёл к концу, и я надеюсь, что он оказался не только полезным, но ещё и интересным.
Желаю успехов!
Решения и ответы:
Пример 10. Решение:
1) Способ первый: нормальное распределения вероятностей задаётся плотностью 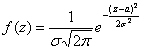 . В нашем случае
. В нашем случае ![]() , и поэтому:
, и поэтому: ![]() на интервале
на интервале ![]() . И из функции
. И из функции ![]() легко усмотреть, что
легко усмотреть, что ![]() на отрезке
на отрезке ![]() и
и ![]() вне этого отрезка.
вне этого отрезка.
И здесь ОБЯЗАТЕЛЬНО нужно проконтролировать, что:
![]() – функция
– функция ![]() действительно задаёт плотность распределения.
действительно задаёт плотность распределения.
Способ второй. Используем формулы:
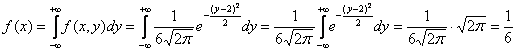 , если
, если ![]() и
и ![]() при иных значениях
при иных значениях ![]() .
.

Вывод: так как ![]() , то случайные величины
, то случайные величины ![]() независимы.
независимы.
2) Вычислим матожидания и дисперсии случайных величин ![]() . Функция
. Функция ![]() задаёт равномерное распределение вероятностей и по соответствующим формулам:
задаёт равномерное распределение вероятностей и по соответствующим формулам:
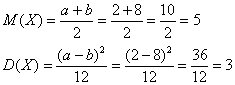
Примечание: разумеется, здесь можно использовать и общие формулы матожидания и дисперсии.
Характеристика компоненты ![]() известны из самой функции плотности:
известны из самой функции плотности:
![]()
По свойствам математического ожидания:
![]()
второе слагаемое выразим из формулы ![]()
![]()
Для независимых случайных величин справедливо свойство ![]() , поэтому:
, поэтому:
![]()
По свойствам дисперсии и формуле ![]() :
:
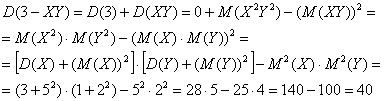
Пример 11. Решение:
Найдём безусловную плотность распределения случайной величины ![]() :
:
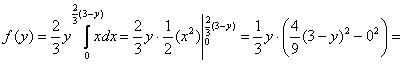
![]() и
и ![]() при иных значениях
при иных значениях ![]() .
.
! Самостоятельно проверяем, что ![]() .
.
Вычислим матожидание:
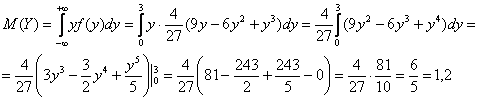
Дисперсию вычислим по формуле:
![]()
В данном случае:
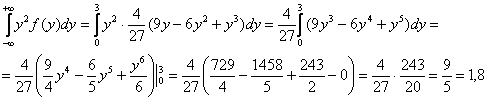
и:
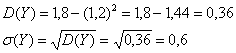
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright