Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»

Учимся решать:

Лекции-уроки по высшей математике для первого курса

Высшая математика для чайников, или с чего начать?
Повторяем школьный курс

Аналитическая геометрия:

Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида

Элементы высшей алгебры:

Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы

Пределы:

Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория

Производные функций:

Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных

Функции и графики:

Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи

ФНП:

Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов

Интегралы:

Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Карта сайта

Лекции-уроки по высшей математике для второго курса

Дифференциальные уравнения:

Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты

Числовые ряды:

Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности

Функциональные ряды:

Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений

Кратные интегралы:

Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы

Элементы векторного анализа:

Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса

Комплексный анализ:

ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?

Теория вероятностей:

Математическая статистика:

Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

Ряды для чайников. Примеры решений

Всех выживших приветствую на втором курсе! На этом уроке, а точнее, на серии уроков, мы научимся управляться с рядами. Тема не очень сложная, но для ее освоения потребуются знания с первого курса, в частности, необходимо понимать, что такое предел, и уметь находить простейшие пределы. Впрочем, ничего страшного, по ходу объяснений я буду давать соответствующие ссылки на нужные уроки. Некоторым читателям тема математических рядов, приемы решения, признаки, теоремы могут показаться своеобразными, и даже вычурными, нелепыми. В этом случае не нужно сильно «загружаться», принимаем факты такими, какими они есть, и просто учимся решать типовые, распространенные задания.

Понятие числового ряда

В общем виде числовой ряд можно записать так: .
Здесь:
– математический значок суммы;
– общий член ряда (запомните этот простой термин);
– переменная-«счётчик». Запись обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас , затем , потом , и так далее – до бесконечности. Вместо переменной иногда используется переменная или . Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля , с двойки либо с любого натурального числа.

В соответствии с переменной-«счётчиком» любой ряд можно расписать развёрнуто:
– и так далее, до бесконечности.

Cлагаемые – это ЧИСЛА, которые называются членами ряда. Если все они неотрицательны (больше либо равны нулю), то такой ряд называют положительным числовым рядом.

Пример 1

Записать первые три члена ряда

Это уже, кстати, «боевое» задание – на практике довольно часто требуется записать несколько членов ряда.

Сначала , тогда:
Затем , тогда:
Потом , тогда:

Процесс можно продолжить до бесконечности, но по условию требовалось написать первые три члена ряда, поэтому записываем ответ:

Обратите внимание на принципиальное отличие от числовой последовательности,
в которой члены не суммируются, а рассматриваются как таковые.

Пример 2

Записать первые три члена ряда

Это пример для самостоятельного решения, ответ в конце урока

Даже для сложного на первый взгляд ряда не составляет трудности расписать его в развернутом виде:

Пример 3

Записать первые три члена ряда

На самом деле задание выполняется устно: мысленно подставляем в общий член ряда сначала , потом и . В итоге:

Ответ оставляем в таком виде, полученные члены ряда лучше не упрощать, то есть не выполнять действия: , , . Почему? Ответ в виде гораздо проще и удобнее проверять преподавателю.

Иногда встречается обратное задание

Пример 4

Записать сумму в свёрнутом виде с общим членом ряда

Здесь нет какого-то четкого алгоритма решения, закономерность нужно просто увидеть.
В данном случае:

Для проверки полученный ряд можно «расписать обратно» в развернутом виде.

А вот пример чуть сложнее для самостоятельного решения:

Пример 5

Записать сумму в свёрнутом виде с общим членом ряда

Выполнить проверку, снова записав ряд в развернутом виде

Сходимость числовых рядов

Одной из ключевых задач темы является исследование ряда на сходимость. При этом возможны два случая:

1) Ряд расходится. Это значит, что бесконечная сумма равна бесконечности: либо суммы вообще не существует, как, например, у ряда
(вот, кстати, и пример ряда с отрицательными членами). Хороший образец расходящегося числового ряда встретился в начале урока: . Здесь совершенно очевидно, что каждый следующий член ряда больше, чем предыдущий, поэтому и, значит, ряд расходится. Ещё более тривиальный пример: .

2) Ряд сходится. Это значит, что бесконечная сумма равна некоторому конечному числу : . Пожалуйста: – этот ряд сходится и его сумма равна нулю. В качестве более содержательного примера можно привести бесконечно убывающую геометрическую прогрессию, известную нам ещё со школы: . Сумма членов бесконечно убывающей геометрической прогрессии рассчитывается по формуле: , где – первый член прогрессии, а – её основание, которое, как правило, записывают в виде правильной дроби. В данном случае: , . 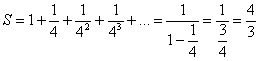Таким образом: Получено конечное число, значит, ряд сходится, что и требовалось доказать.

Однако в подавляющем большинстве случаев найти сумму ряда не так-то просто, и поэтому на практике для исследования сходимости ряда используют специальные признаки, которые доказаны теоретически.

Существует несколько признаков сходимости ряда: необходимый признак сходимости ряда, признаки сравнения, признак Даламбера, признаки Коши, признак Лейбница и некоторые другие признаки. Когда какой признак применять? Это зависит от общего члена ряда , образно говоря – от «начинки» ряда. И очень скоро мы всё разложим по полочкам.

! Для дальнейшего усвоения урока необходимо хорошо понимать, что такое предел и хорошо уметь раскрывать неопределенность вида . Для повторения или изучения материала обратитесь к статье Пределы. Примеры решений.

Необходимый признак сходимости ряда

Если ряд сходится, то его общий член стремится к нулю: .

Обратное в общем случае неверно, т.е., если , то ряд может как сходиться, так и расходиться. И поэтому этот признак используют для обоснования расходимости ряда:

Если общий член ряда не стремится к нулю, то ряд расходится

Или короче: если , то ряд расходится. В частности, возможна ситуация, когда предела не существует вообще, как, например, предела . Вот сразу и обосновали расходимость одного ряда :)

Но гораздо чаще предел расходящегося ряда равен бесконечности, при этом в качестве «динамической» переменной вместо «икса» выступает . Освежим наши знания: пределы с «иксом» называют пределами функций, а пределы с переменной «эн» – пределами числовых последовательностей. Очевидное отличие состоит в том, что переменная «эн» принимает дискретные (прерывные) натуральные значения: 1, 2, 3 и т.д. Но данный факт мало сказывается на методах решения пределов и способах раскрытия неопределенностей.

Докажем, что ряд из первого примера расходится.
Общий член ряда:

Вывод: ряд расходится, так как не выполнен необходимый признак сходимости ряда.

Необходимый признак часто применяется в реальных практических заданиях:

Пример 6

Исследовать ряд на сходимость

В числителе и знаменателе у нас находятся многочлены. Тот, кто внимательно прочитал и осмыслил метод раскрытия неопределенности в статье Пределы. Примеры решений, наверняка уловил, что когда старшие степени числителя и знаменателя равны, тогда предел равен конечному числу.

Решаем:

Делим числитель и знаменатель на

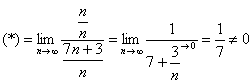
Исследуемый ряд расходится, так как не выполнен необходимый признак сходимости ряда.

Готово.

Пример 7

Исследовать ряд на сходимость

Это пример для самостоятельного решения. Полное решение и ответ в конце урока

Итак, когда нам дан ЛЮБОЙ числовой ряд, в первую очередь проверяем (мысленно или на черновике): а стремится ли его общий член к нулю? Если не стремится – оформляем решение по образцу примеров № 6, 7 и даём ответ о том, что ряд расходится.

Какие типы очевидно расходящихся рядов мы рассмотрели? Сразу понятно, что расходятся ряды вроде или . Также расходятся ряды из примеров № 6, 7: когда в числителе и знаменателе находятся многочлены, и старшая степень числителя больше либо равна старшей степени знаменателя. Во всех этих случаях при решении и оформлении примеров мы используем необходимый признак сходимости ряда.

Почему признак называется необходимым? Понимайте самым естественным образом: для того, чтобы ряд сходился, необходимо, чтобы его общий член стремился к нулю. И всё бы было отлично, но этого ещё не достаточно. Иными словами, если общий член ряда стремится к нулю, ТО ЭТО ЕЩЕ НЕ ЗНАЧИТ, что ряд сходится – он может, как сходиться, так и расходиться!

Знакомьтесь:

Данный ряд называется гармоническим рядом. Пожалуйста, запомните! Среди числовых рядов он является прима-балериной. Точнее, балеруном =)

Легко заметить, что , НО. В теории математического анализа доказано, что гармонический ряд расходится.

Также следует запомнить понятие обобщенного гармонического ряда:

1) Данный ряд расходится при . Например, расходятся ряды , , .
2) Данный ряд сходится при . Например, сходятся ряды , , . Еще раз подчеркиваю, что почти во всех практических заданиях нам совершенно не важно, чему равна сумма, например, ряда , важен сам факт его сходимости.

Это элементарные факты из теории рядов, которые уже доказаны, и при решении какого-нибудь практического примера можно смело ссылаться, например, на расходимость ряда или сходимость ряда .

Вообще, рассматриваемый материал очень похож на исследование несобственных интегралов, и тому, кто изучал эту тему, будет легче. Ну а тому, кто не изучал – легче вдвойне:)

Итак, что делать, если общий член ряда СТРЕМИТСЯ к нулю? В таких случаях для решения примеров нужно использовать другие, достаточные признаки сходимости / расходимости:

Признаки сравнения для положительных числовых рядов

Заостряю ваше внимание, что здесь речь уже идёт только о положительных числовых рядах (с неотрицательными членами).

Существуют два признака сравнения, один из них я буду называть просто признаком сравнения, другой – предельным признаком сравнения.

Сначала рассмотрим признак сравнения, а точнее, первую его часть:

Рассмотрим два положительных числовых ряда и . Если известно, что ряд – сходится, и, начиная с некоторого номера , выполнено неравенство , то ряд тоже сходится.

Иными словами: Из сходимости ряда с бОльшими членами следует сходимость ряда с меньшими членами. На практике неравенство часто выполнено вообще для всех значений :

Пример 8

Исследовать ряд на сходимость

Во-первых, проверяем (мысленно либо на черновике) выполнение необходимого признака сходимости:
, а значит, «отделаться малой кровью» не удалось.

Внимание! Далее такая проверка будет подразумеваться по умолчанию, и далее я на этом не останавливаюсь!

Заглядываем в «пачку» обобщенного гармонического ряда и, ориентируясь на старшую степень, находим похожий ряд: Из теории известно, что он сходится.

Для всех натуральных номеров справедливо очевидное неравенство:

а бОльшим знаменателям соответствуют мЕньшие дроби:
, значит, по признаку сравнения исследуемый ряд сходится вместе с рядом .

Готово.

Если у вас есть какие-то сомнения, то неравенство всегда можно расписать подробно! Распишем построенное неравенство для нескольких номеров «эн»:
Если , то
Если , то
Если , то
Если , то
….
и теперь-то уж совершенно понятно, что неравенство выполнено для всех натуральных номеров «эн».

Проанализируем признак сравнения и решенный пример с неформальной точки зрения. Все-таки, почему ряд сходится? А вот почему. Если ряд сходится, то он имеет некоторую конечную сумму : . И поскольку все члены ряда меньше соответствующих членов ряда , то ясен пень, что сумма ряда не может быть больше числа , и тем более, не может равняться бесконечности!

Аналогично можно доказать сходимость «похожих» рядов: , , и т.д.

! Обратите внимание, что во всех случаях в знаменателях у нас находятся «плюсы». Наличие хотя бы одного минуса может серьёзно осложнить использование рассматриваемого признака сравнения. Например, если ряд таким же образом сравнить со сходящимся рядом ( выпишите несколько неравенств для первых членов), то условие не будет выполняться вообще! Здесь можно извернуться и подобрать для сравнения другой сходящийся ряд, например, , но это повлечёт за собой лишние оговорки и другие ненужные трудности. Поэтому для доказательства сходимости ряда гораздо проще использовать предельный признак сравнения (см. следующий параграф).

Пример 9

Исследовать ряд на сходимость

И в этом примере я предлагаю вам самостоятельно рассмотреть вторую часть признака сравнения:

Если известно, что ряд – расходится, и, начиная с некоторого номера (часто с самого первого), выполнено неравенство , то ряд тоже расходится.

Иными словами: Из расходимости ряда с меньшими членами следует расходимость ряда с бОльшими членами.

Что нужно сделать?
Нужно сравнить исследуемый ряд с расходящимся гармоническим рядом . Для лучшего понимания постройте несколько конкретных неравенств и убедитесь в справедливаости неравенства .

Решение и образец оформления в конце урока.

Как уже отмечалось, на практике только что рассмотренный признак сравнения применяют редко. Настоящей «рабочей лошадкой» числовых рядов является предельный признак сравнения, и по частоте использования с ним может конкурировать разве что признак Даламбера.

Предельный признак сравнения числовых положительных рядов

Рассмотрим два положительных числовых ряда и . Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу : , то оба ряда сходятся или расходятся одновременно.

Когда применяется предельный признак сравнения? Предельный признак сравнения применяется тогда, когда «начинкой» ряда у нас являются многочлены. Либо один многочлен в знаменателе, либо многочлены и в числителе и в знаменателе. Опционально многочлены могут находиться под корнями.

Разделаемся с рядом, для которого забуксовал предыдущий признак сравнения.

Пример 10

Исследовать ряд на сходимость

Сравним данный ряд со сходящимся рядом . Используем предельный признак сравнения. Известно, что ряд – сходится. Если нам удастся показать, что равен конечному, отличному от нуля числу, то будет доказано, что ряд – тоже сходится.

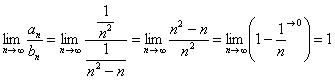
Получено конечное, отличное от нуля число, значит, исследуемый ряд сходится вместе с рядом .

Почему для сравнения был выбран именно ряд ? Если бы мы выбрали любой другой ряд из «обоймы» обобщенного гармонического ряда, то у нас не получилось бы в пределе конечного, отличного от нуля числа (можете поэкспериментировать).

Примечание: когда мы используем предельный признак сравнения, не имеет значения, в каком порядке составлять отношение общих членов, в рассмотренном примере отношение можно было составить наоборот: 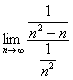– это не изменило бы сути дела.

Предельный признак сравнения применим почти для всех рядов, которые мы рассмотрели в предыдущем пункте:
, , , .
Данные ряды по только что рассмотренной трафаретной схеме нужно предельно сравнить соответственно со сходящимися рядами:
, , , .

Пример 11

Исследовать ряд на сходимость

Это пример для самостоятельного решения.

Что делать, если многочлены находятся и в знаменателе, и в числителе? Алгоритм решения почти такой же – нам нужно подобрать для сравнения подходящий ряд из «обоймы» обобщенного гармонического ряда.

Пример 12

Исследовать ряд на сходимость

Мы видим, что и в числителе и в знаменателе у нас многочлены, причем, в знаменателе многочлен находится под корнем. Подбираем ряд для сравнения .

1) Сначала нужно найти старшую степень знаменателя. Если бы не было корня, то, понятно, что старшая степень знаменателя равнялась бы четырем. Что делать, когда есть корень? Об этом я уже рассказывал на уроке Методы решения пределов. Повторение – мать учения: мысленно или на черновике отбрасываем все члены, кроме старшего: . Если есть константа, её тоже отбрасываем: . Теперь извлекаем корень: . Таким образом, старшая степень знаменателя равна двум.

2) Выясняем старшую степень числителя. Очевидно, что она равна единице.

3) Из старшей степени знаменателя вычитаем старшую степень числителя: 2 – 1 = 1

Таким образом, наш ряд нужно сравнить с рядом , то есть, с расходящимся гармоническим рядом.

По мере накопления опыта решения эти три пункта можно и нужно проводить мысленно.

Само оформление решения должно выглядеть примерно так:

”
Сравним данный ряд с расходящимся гармоническим рядом . Используем предельный признак сравнения:

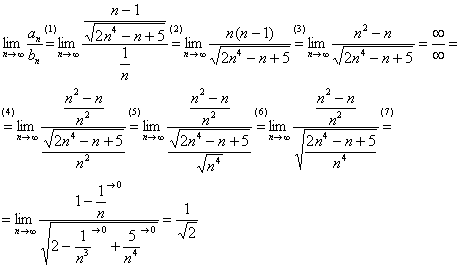
Получено конечное, отличное от нуля число, значит, исследуемый ряд расходится вместе с гармоническим рядом .

”

(1) Составляем отношение общих членов.
(2) Избавляемся от четырехэтажности дроби.
(3) Раскрываем в числителе скобки.
(4) Неопределенность устраняем стандартным способом деления числителя и знаменателя на «эн» в старшей степени.
(5) В самой нижней строке подготавливаем для внесения под корень:
(6) В знаменателе организуем общий корень.
Примечание: на практике пункты 5,6 можно пропустить, я их очень подробно разжевал для тех, кто не очень понимает, как обращаться с корнями.
(7) Почленно делим числители на знаменатели. Помечаем члены, которые стремятся к нулю.

Пример 13

Исследовать ряд на сходимость

Это пример для самостоятельного решения.

В недалёком будущем вы будете сразу видеть, сходится такой ряд или расходится. Например, рассмотрим ряд . Ага, 3 – 1 = 2, значит, ряд нужно сравнить со сходящимся рядом , и сразу можно сказать, что наш исследуемый ряд тоже сходится. Дело за малым – осталось аккуратно оформить стандартное рутинное решение.

Вот, пожалуй, и все начальные сведения о положительных числовых рядах, которые потребуются вам при решении практических примеров. Следующий урок по теме числовых рядов – Признаки сходимости рядов. Признак Даламбера. Признаки Коши

Желаю успехов!

Решения и ответы:

Пример 2:

Примечание: обратите внимание, что переменная-«счётчик» в данном примере «заряжается» со значения

Пример 5:

Пример 7: Проверим выполнение необходимого признака сравнения:

Делим числитель и знаменатель на

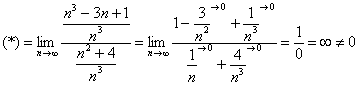
Исследуемый ряд расходится, так как не выполнен необходимый признак сходимости ряда.

Пример 9: Сравним данный ряд с расходящимся гармоническим рядом . Для любого номера выполнено неравенство , а меньшим знаменателям соответствуют бОльшие дроби:
, значит, по признаку сравнения исследуемый ряд расходится вместе с гармоническим рядом.

Примечание: и здесь тоже есть неформальный смысл. Так как гармонический ряд расходится, то сумма его членов: . Мы показали, что члены ряда ещё больше членов ряда , и совершенно понятно, что сумма ряда не может быть меньше бесконечности.

Пример 11: Сравним данный ряд с расходящимся рядом . Используем предельный признак сравнения:

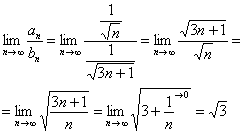
Получено конечное, отличное от нуля число, значит, исследуемый ряд расходится вместе с рядом .

Пример 13: Эти три пункта выполняем мысленно или на черновике:
1) Старшая степень знаменателя:4
2) Старшая степень числителя: 1
3) 4 – 1 = 3
Сравним данный ряд со сходящимся рядом . Используем предельный признак сравнения: