


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Что такое интеграл? Теория для чайников
После того, как я рассказал о смысле производной, было бы странным оставить без внимания теоретический материал, посвященный интегралам. На данном уроке мы, наконец, узнаем, что же такое неопределённый и определённый интеграл. При этом основной упор будет сделан не на создание всеобъемлющего и солидного справочника по теории (зачем? есть учебники), а на понимание темы. Статья написана простым языком и рассчитана на широкий круг заинтересованных читателей, включая учащихся старших классов.
С чего начать?
Если вы только-только приступили к изучению интегрального исчисления либо неважно в нём ориентируетесь, то я не рекомендую сразу набрасываться на информацию данной страницы. Почему? Классический научный подход предполагает: а) изучение теории, б) решение практических заданий. Всё вроде бы правильно и логично, но… многие по себе знают, как скучно, а порой и тошно вникать в малопонятные определения, свойства, теоремы и как хочется поскорее захлопнуть учебник, конспект – чтобы всего этого больше никогда не видеть. Объяснение очевидно: теоретические знания наиболее эффективно усваиваются через практику. И это закономерно – сама наука своей бОльшей частью сформировалась на основе конкретных примеров из реальной жизни.
Поэтому сначала лучше ознакомиться с основной сутью и терминологией раздела, а также научиться решать. Хотя бы немного, хотя бы чуть-чуть. Следующие три урока позволят вам быстро освоить начальный уровень по неопределённому интегралу:
Неопределённый интеграл. Примеры решений;
Метод замены переменной;
Интегрирования по частям.
Базовые знания по определённому интегралу можно почерпнуть в следующих статьях:
Определённый интеграл. Примеры решений;
Вычисление площади с помощью определённого интеграла.
Далее буду предполагать, что вас не поставят в тупик элементарные термины и простейшие интегралы. Кроме того, желательно ПОНИМАТЬ, что такое предел функции, бесконечно малая величина и производная – только тогда чтение будет по настоящему увлекательным, а усвоение материала – качественным. Возможно, требования повергли «чайников» в уныние... однако опускать руки не нужно – все пробелы закрываются в кратчайшие сроки!
Первообразная функция, неопределённый интеграл и его свойства
К понятию первообразной функции приводят многие задачи математического анализа и физики. Рассмотрим былинный физический пример: известен закон изменения скорости тела ![]() , требуется найти закон изменения координаты
, требуется найти закон изменения координаты ![]() данного тела.
данного тела.
Скорость – это производная от пройдённого пути: ![]() (см. урок о смысле производной), таким образом, для решения задачи необходимо по заданной функции
(см. урок о смысле производной), таким образом, для решения задачи необходимо по заданной функции ![]() (производной) восстановить функцию
(производной) восстановить функцию ![]() .
.
Общая же постановка вопроса такова: в распоряжении есть некоторая функция ![]() и возникает потребность выяснить, от какой функции она произошла. То есть, необходимо найти ТАКУЮ функцию
и возникает потребность выяснить, от какой функции она произошла. То есть, необходимо найти ТАКУЮ функцию ![]() , чтобы
, чтобы ![]() .
.
Определение: функция ![]() называется первообразной для функции
называется первообразной для функции ![]() на некотором промежутке, если для всех
на некотором промежутке, если для всех ![]() из этого промежутка выполняется равенство
из этого промежутка выполняется равенство ![]() или, что то же:
или, что то же: ![]() (раскрывать дифференциал мы научились ещё на первом уроке о неопределённом интеграле).
(раскрывать дифференциал мы научились ещё на первом уроке о неопределённом интеграле).
Например, для ![]() первообразной функцией на всей числовой прямой будет являться функция
первообразной функцией на всей числовой прямой будет являться функция ![]() . И действительно, для любого «икс»:
. И действительно, для любого «икс»:
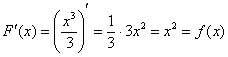 .
.
Простое, но требующее доказательства утверждение:
Теорема: пусть ![]() – какая-нибудь первообразная для функции
– какая-нибудь первообразная для функции ![]() на некотором промежутке. Тогда функция
на некотором промежутке. Тогда функция ![]() , где
, где ![]() – произвольная константа, тоже будет первообразной функцией для
– произвольная константа, тоже будет первообразной функцией для ![]() на данном промежутке.
на данном промежутке.
Доказательство: поскольку производная константы равна нулю, то:
![]() , следовательно,
, следовательно, ![]() – первообразная для функции
– первообразная для функции ![]() по определению первообразной, что и требовалось доказать.
по определению первообразной, что и требовалось доказать.
Так, для функции ![]() первообразной будет являться любая функция из множества
первообразной будет являться любая функция из множества ![]() , где
, где ![]() (мысленно поподставляйте конкретные числовые значения).
(мысленно поподставляйте конкретные числовые значения).
Докажем обратное утверждение: любая другая первообразная ![]() для функции
для функции ![]() отличается от
отличается от ![]() лишь на приплюсованную константу, иными словами:
лишь на приплюсованную константу, иными словами: ![]() .
.
Вот это уже менее очевидный факт. И в самом деле – вдруг для функции ![]() существует не только
существует не только ![]() , а какая-нибудь ещё первообразная?
, а какая-нибудь ещё первообразная?
Пусть ![]() – это две первообразные для функции
– это две первообразные для функции ![]() на некотором промежутке. Тогда для любого «икс» из данного промежутка производная разности будет равна:
на некотором промежутке. Тогда для любого «икс» из данного промежутка производная разности будет равна:
![]() , или если записать короче:
, или если записать короче:
![]()
Но с другой стороны, из дифференциального исчисления известно, что данному условию удовлетворяет функция-константа и только она:
![]()
Откуда и следует равенство ![]() , которое требовалось доказать. Таким образом, любая первообразная для функции
, которое требовалось доказать. Таким образом, любая первообразная для функции ![]() имеет вид
имеет вид ![]()
Вуаля:
Определение: множество всех первообразных ![]() для функции
для функции ![]() называется неопределённым интегралом от функции
называется неопределённым интегралом от функции ![]() и обозначается символом
и обозначается символом ![]() . Таким образом, по определению:
. Таким образом, по определению:
![]() , где
, где ![]()
Напоминаю, что функция ![]() называется подынтегральной функцией,
называется подынтегральной функцией, ![]() – подынтегральным выражением, а сам процесс отыскания множества первообразных
– подынтегральным выражением, а сам процесс отыскания множества первообразных ![]() – интегрированием. Интегрирование – это восстановление функции
– интегрированием. Интегрирование – это восстановление функции ![]() по её производной
по её производной ![]() (обратное действие по отношению к дифференцированию).
(обратное действие по отношению к дифференцированию).
Для нашего демонстрационного примера:
![]() , где
, где ![]()
Проверка: 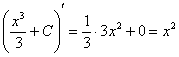 – исходная подынтегральная функция.
– исходная подынтегральная функция.
Любая ли функция интегрируема? Нет.
Сформулируем достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.
Как видите, условие довольно-таки лояльное – для существования первообразной достаточно лишь непрерывности. Ниже по тексту, если не сказано иного, все функции будем считать интегрируемыми.
Свойства неопределённого интеграла
Нумеровать крайне не люблю, но здесь лучшего варианта не видно:
1) Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению:
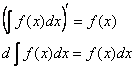
Доказательство: по определению неопределённого интеграла: ![]() , следовательно:
, следовательно:
![]() , что и требовалось доказать.
, что и требовалось доказать.
Второе. По правилу раскрытия дифференциала (а точнее, по определению дифференциала) и только что доказанному пункту:
![]()
Потёрто.
2) Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
![]()
Учитывая, что ![]() , свойство можно переписать в следующем виде:
, свойство можно переписать в следующем виде:
![]()
Тут даже доказывать ничего не надо, поскольку ![]() и получается непосредственно само определение неопределённого интеграла.
и получается непосредственно само определение неопределённого интеграла.
Как видите, в обоих случаях значки дифференциала и интеграла взаимно уничтожаются, что естественно.
Следующие два пункта вам хорошо знакомы – это мировое свойство линейности, которое справедливо и для других типов интегралов: определённых, двойных, тройных, криволинейных и пр.
3) Константу можно вынести из-под знака интеграла
То есть, если ![]() , то
, то ![]()
Доказательство: а вы как думали? =)
Найдём производную левой части. Используем свойство № 1:
![]()
Найдём производную правой части. Используем правило дифференцирования ![]() и свойство № 1:
и свойство № 1:
![]()
Получены одинаковые результаты, из чего и следует справедливость данного свойства.
Вообще, многие доказательства не столько сложны, сколько занудны и формальны – используются определения, ранее доказанные свойства, теоремы и т.д. Но, несмотря на их сухость, немалая часть студентов входит во вкус и даже начинает читать учебники по высшей математике в любой свободный момент =) Будьте осторожны =)
4) Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов:
![]()
Справедливо для любого количества слагаемых.
Свойство проверяется точно так же, как и предыдущее – берутся производные от обеих частей. Но доказывать его я, пожалуй, не буду – хорошего понемножку =)
Перейдём к ещё более интересному разделу:
Определённый интеграл и его свойства
Настал момент, который все ждали, затаив дыхание. Что такое определённый интеграл 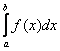 и почему он есть площадь? Да и откуда взялся сам значок интеграла? Вот мы много раз слышали: «интеграл, интеграл, интеграл, …». Но понятие же не из космоса прилетело! Читаем:
и почему он есть площадь? Да и откуда взялся сам значок интеграла? Вот мы много раз слышали: «интеграл, интеграл, интеграл, …». Но понятие же не из космоса прилетело! Читаем:
Пусть функция ![]() определена на промежутке
определена на промежутке ![]() . Для определённости и простоты считаем, что функция положительна
. Для определённости и простоты считаем, что функция положительна ![]() и непрерывна на данном отрезке. Поставим задачу найти площадь
и непрерывна на данном отрезке. Поставим задачу найти площадь ![]() криволинейной трапеции, ограниченной графиком функции
криволинейной трапеции, ограниченной графиком функции ![]() , прямыми
, прямыми ![]() и осью
и осью ![]() . Обращаю внимание на тот факт, что непрерывность функции на отрезке заведомо гарантирует существование конечной площади
. Обращаю внимание на тот факт, что непрерывность функции на отрезке заведомо гарантирует существование конечной площади ![]() .
.
Разобьём отрезок ![]() на
на ![]() частей следующими точками:
частей следующими точками:
![]() (красные точки):
(красные точки):
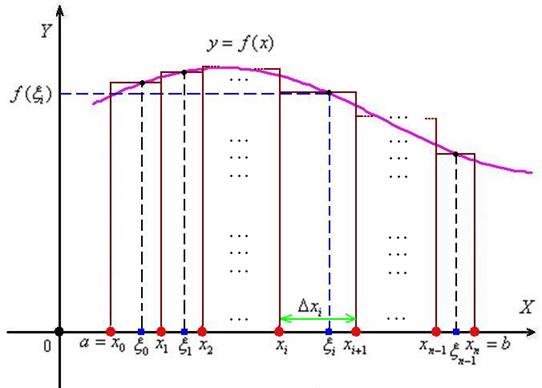
В результате получено ![]() частичных промежутков
частичных промежутков ![]() с длинами
с длинами ![]() соответственно. В общем случае длины различны – какие-то отрезки короче, какие-то длиннее. Максимальную длину называют диаметром разбиения и обозначают буквой «лямбда»:
соответственно. В общем случае длины различны – какие-то отрезки короче, какие-то длиннее. Максимальную длину называют диаметром разбиения и обозначают буквой «лямбда»: ![]() .
.
Примечание: последняя запись читается, как «максимальное значение из множества (набора) ![]() »
»
В каждом из полученных промежутков опять же произвольно выбираем точки ![]() (синие квадратики).
(синие квадратики).
Примечание: ![]() («кси») – 14-я буква греческого алфавита
(«кси») – 14-я буква греческого алфавита
Рассмотрим ![]() промежуток
промежуток ![]() . Его длина, очевидно, равна
. Его длина, очевидно, равна ![]() (зелёная обоюдоострая линия). Значению аргумента
(зелёная обоюдоострая линия). Значению аргумента ![]() соответствует значение функции
соответствует значение функции ![]() (синие пунктирные линии), и произведение
(синие пунктирные линии), и произведение ![]() в точности равно площади соответствующего коричневого прямоугольника.
в точности равно площади соответствующего коричневого прямоугольника.
Аналогично устроен каждый отрезок. Составим сумму, которая равна площади коричневой ступенчатой фигуры:
![]()
Данная сумма называется интегральной суммой, и её часто записывают в свёрнутом виде:
![]()
Примечание: ![]() – это значок суммы, а переменная
– это значок суммы, а переменная ![]() – своеобразный «счётчик», т.е. сначала
– своеобразный «счётчик», т.е. сначала ![]() , затем
, затем ![]() , потом
, потом ![]() , … и, наконец,
, … и, наконец, ![]()
Что означает прилагательное «интегральной»? В широком смысле слова, интегрировать – это значит, что-то объединять. В данном случае интегральная сумма ![]() объединяет площади коричневых прямоугольников и с некоторой точностью приближает площадь криволинейной трапеции:
объединяет площади коричневых прямоугольников и с некоторой точностью приближает площадь криволинейной трапеции: ![]()
Теперь зададимся вопросом: как улучшить точность приближения? Действия очевидны – увеличиваем и увеличиваем значение ![]() . При этом количество отрезков
. При этом количество отрезков ![]() растёт, а их длины
растёт, а их длины ![]() – уменьшаются, в том числе неизбежно уменьшается и максимальная длина
– уменьшаются, в том числе неизбежно уменьшается и максимальная длина ![]() . Количество точек
. Количество точек ![]() тоже возрастает и ступенчатая фигура всё больше и больше напоминает криволинейную трапецию.
тоже возрастает и ступенчатая фигура всё больше и больше напоминает криволинейную трапецию.
И, если количество отрезков разбиения устремить к бесконечности ![]() , то интегральная сумма (площадь ступенчатой фигуры) будет стремиться к площади криволинейной трапеции:
, то интегральная сумма (площадь ступенчатой фигуры) будет стремиться к площади криволинейной трапеции: ![]() .
.
Таким образом, площадь криволинейной трапеции равна пределу интегральной суммы при диаметре разбиения, стремящемся к нулю:
![]()
Наблюдаем за удивительным превращением:
1) В рассматриваемом контексте сумму ![]() ещё с 17 века обозначали растянутой буквой S (Summa). Это обозначение известно как значок интеграла:
ещё с 17 века обозначали растянутой буквой S (Summa). Это обозначение известно как значок интеграла:
![]()
2) Если ![]() (и, следовательно,
(и, следовательно, ![]() ), то значения
), то значения ![]() стремятся «покрыть» все значения функции
стремятся «покрыть» все значения функции ![]() из промежутка
из промежутка ![]() , то есть:
, то есть:
![]() , при этом пределы интегрирования:
, при этом пределы интегрирования: ![]()
3) И, наконец, длина любого промежуточного отрезка ![]() становится бесконечно малой. Обозначение этой бесконечно малой длины мы тоже хорошо знаем, оно указывает, что объединение ведётся по переменной «икс»:
становится бесконечно малой. Обозначение этой бесконечно малой длины мы тоже хорошо знаем, оно указывает, что объединение ведётся по переменной «икс»:
![]()
В результате, площадь криволинейной трапеции: 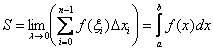
Определение: конечный предел интегральной суммы ![]() при
при ![]() , не зависящий ни от способа дробления отрезка
, не зависящий ни от способа дробления отрезка ![]() , ни от выбора точек
, ни от выбора точек ![]() , называется определённым интегралом функции
, называется определённым интегралом функции ![]() по промежутку
по промежутку ![]() и обозначается символом
и обозначается символом 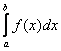 .
.
При этом функция ![]() называется интегрируемой в промежутке
называется интегрируемой в промежутке ![]() . Для интегрируемости (а, значит, существования конечной площади), напоминаю, достаточно непрерывности функции на отрезке
. Для интегрируемости (а, значит, существования конечной площади), напоминаю, достаточно непрерывности функции на отрезке ![]() . Если же на данном промежутке есть участки, где функция, например, не определена (нет её графика), то конечного предела
. Если же на данном промежутке есть участки, где функция, например, не определена (нет её графика), то конечного предела ![]() и, соответственно, определённого интеграла
и, соответственно, определённого интеграла 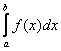 не существует.
не существует.
По аналогичному принципу (дробление отрезка, выбор промежуточных точек, нахождение интегральной суммы, предел и предельный переход) выводятся другие тематические формулы: объема тела вращения, длины дуги кривой, площади поверхности вращения и т. д. Надеюсь, теперь вам будет значительно легче разобраться в соответствующем теоретическом материале.
Если что-то осталось недопонятым, текст следует не спеша перечитать заново либо вернуться к нему позже. Наиболее вероятные затруднения здесь связаны с альфой и омегой математического анализа – предельным переходом; в этом случае советую основательно проштудировать статьи о пределах и теории производной функции.
Всё было бы хорошо, но формулу 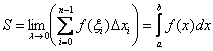 очень трудно применить на практике (даже для простых функций), поэтому возникает задача отыскания более эффективного пути расчёта площади. И такой путь действительно существует – ведь из определения определённого интеграла следует, что он не зависит от способа разбиения промежутка
очень трудно применить на практике (даже для простых функций), поэтому возникает задача отыскания более эффективного пути расчёта площади. И такой путь действительно существует – ведь из определения определённого интеграла следует, что он не зависит от способа разбиения промежутка ![]() и от выбора точек
и от выбора точек ![]() . Важен лишь только нижний предел интегрирования «а», верхний предел интегрирования «бэ» и сама функция «эф от икс».
. Важен лишь только нижний предел интегрирования «а», верхний предел интегрирования «бэ» и сама функция «эф от икс».
Вывод формулы Ньютона-Лейбница
Рассмотрим тот же график ![]() и познакомимся с функцией переменной площади
и познакомимся с функцией переменной площади ![]() . Что это за функция? Зафиксируем произвольную точку
. Что это за функция? Зафиксируем произвольную точку ![]() (левая красная точка), лежащую между точками «а» и «бэ»:
(левая красная точка), лежащую между точками «а» и «бэ»:
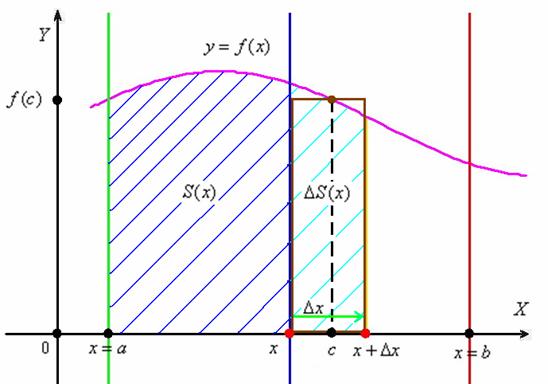
В данной точке функция ![]() равна площади криволинейной трапеции, которая расположена между зелёной и синей линиями и заштрихована синим цветом. Мысленно начните уменьшать значение «икс» и сдвигать синюю прямую влево – площадь
равна площади криволинейной трапеции, которая расположена между зелёной и синей линиями и заштрихована синим цветом. Мысленно начните уменьшать значение «икс» и сдвигать синюю прямую влево – площадь ![]() начнёт уменьшаться и, в конце концов, в точке
начнёт уменьшаться и, в конце концов, в точке ![]() станет равной нулю:
станет равной нулю: ![]() (прямые совпадут). Теперь возвращаемся на исходную позицию и сдвигаем синюю линию вправо – в этом случае площадь
(прямые совпадут). Теперь возвращаемся на исходную позицию и сдвигаем синюю линию вправо – в этом случае площадь ![]() начнёт расти. И когда мы достигнем верхнего предела
начнёт расти. И когда мы достигнем верхнего предела ![]() (синяя прямая «закроет» красную), площадь будет равна в точности площади всей криволинейной трапеции:
(синяя прямая «закроет» красную), площадь будет равна в точности площади всей криволинейной трапеции: ![]() .
.
Таким образом, аргумент может изменяться в пределах ![]() , при этом функция
, при этом функция ![]() (площадь) будет возрастать от
(площадь) будет возрастать от ![]() до
до ![]() .
.
Докажем, что функция переменной площади ![]() является первообразной функцией для функции
является первообразной функцией для функции ![]() , то есть докажем, что
, то есть докажем, что ![]() .
.
Вернёмся к нашей точке «икс» и зададим в ней приращение ![]() (зелёная стрелка). Для определённости полагаем, что
(зелёная стрелка). Для определённости полагаем, что ![]() (случай
(случай ![]() доказывается аналогично). Приращение аргумента
доказывается аналогично). Приращение аргумента ![]() влечёт приращение функции
влечёт приращение функции ![]() – геометрически это площадь криволинейной трапеции, которая заштрихована голубым цветом.
– геометрически это площадь криволинейной трапеции, которая заштрихована голубым цветом.
По так называемой теореме о среднем, на отрезке ![]() существует точка «цэ» – такая, что площадь коричневого прямоугольника равна площади голубой трапеции:
существует точка «цэ» – такая, что площадь коричневого прямоугольника равна площади голубой трапеции:
![]()
Примечание: этот участок чертежа схематичен, поскольку мне трудно подобрать идеально точное местоположение точки «цэ»
По определению производной, производная функции – это отношение приращения функции ![]() к приращению аргумента
к приращению аргумента ![]() при
при ![]() :
:
![]() .
.
И, ввиду равенства ![]() :
:
![]()
(*) Так как ![]() , то точка «цэ» бесконечно близко приближается к точке «икс», и, соответственно:
, то точка «цэ» бесконечно близко приближается к точке «икс», и, соответственно: ![]()
Таким образом, для любого ![]() из рассматриваемого промежутка справедливо равенство
из рассматриваемого промежутка справедливо равенство ![]() , означающее, что функция
, означающее, что функция ![]() является первообразной для функции
является первообразной для функции ![]() .
.
По теореме, доказанной в самом начале урока, множество всех первообразных представимо в виде ![]() (отличаются друг от дружки константой).
(отличаются друг от дружки константой).
Теперь в данное равенство подставляем ![]() и соответствующее значение площади
и соответствующее значение площади ![]() :
:
![]() , откуда следует, что
, откуда следует, что ![]()
Найденное значение константы ![]() подставляем в
подставляем в ![]() :
:
![]()
Выруливаем на финишную прямую. При ![]() функция
функция ![]() принимает значение, равное площади всей криволинейной трапеции:
принимает значение, равное площади всей криволинейной трапеции: ![]() . Подставим
. Подставим ![]() и
и ![]() в уравнение
в уравнение ![]() :
:
![]()
Следует отметить, что в учебниках по высшей математике вывод этой формулы проводится в более солидном ключе – с помощью интеграла с переменным верхним пределом. Я же ограничился упрощенной версией доказательства, чтобы материал был понятен бОльшему количеству читателей.
Это ещё, кстати, не всё =) Завершаем мысль:
В предыдущем параграфе мы доказали, что площадь криволинейной трапеции – есть предел интегральной суммы: 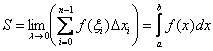 .
.
Но с другой стороны, ![]() .
.
И из этих двух фактов следует лаконичная формула Ньютона-Лейбница:
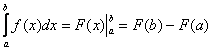 , где
, где ![]() – первообразная функция для функции
– первообразная функция для функции ![]() .
.
Множество практических примеров на применение формулы можно найти в статьях Определённый интеграл. Примеры решений и Вычисление площади с помощью определённого интеграла, а также в последующих статьях раздела.
Рассмотрим основные свойства определённого интеграла
У меня нет цели копипастить учебники, и я остановлюсь только на тех свойствах, которые имеют существенное значение для практики. Нумерация, пожалуй, ни к чему:
– Свойство, которое уже фигурировало в предыдущем пункте: интеграл с одинаковыми пределами интегрирования равен нулю: 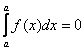 . Графическая интерпретация очевидна: криволинейная трапеция вырождается в отрезок, а площадь отрезка с геометрической точки зрения равна нулю.
. Графическая интерпретация очевидна: криволинейная трапеция вырождается в отрезок, а площадь отрезка с геометрической точки зрения равна нулю.
– Свойство линейности:
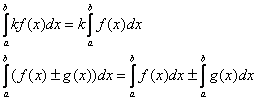
Уважительно промолчим.
– Если у интеграла поменять местами пределы интегрирования, то он сменит знак:
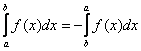
Почему? Пусть для определённости ![]() . Тогда при перестановке пределов интегрирования разбиение отрезка
. Тогда при перестановке пределов интегрирования разбиение отрезка ![]() будет проводиться справа налево (вспоминаем ступенчатую фигуру 1-го чертёжа), и длины частичных промежутков формально станут отрицательными
будет проводиться справа налево (вспоминаем ступенчатую фигуру 1-го чертёжа), и длины частичных промежутков формально станут отрицательными ![]() , поэтому интегральная сумма
, поэтому интегральная сумма ![]() и сам интеграл (как предел суммы) сменит знак.
и сам интеграл (как предел суммы) сменит знак.
Следует заметить, что на практике намного чаще пользуются вторым случаем – когда изначально ![]() , например:
, например:
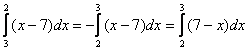
Цель этих действий – расставить пределы интегрирования в привычном порядке, хотя исходный интеграл 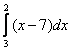 и так рассчитывается без всяких проблем. Однако не редкость, когда перестановка пределов интегрирования не только удобна, но и рациональна.
и так рассчитывается без всяких проблем. Однако не редкость, когда перестановка пределов интегрирования не только удобна, но и рациональна.
– Свойство аддитивности. Какими бы ни были точки ![]() :
:
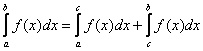
Здесь в первую очередь, конечно же, напрашивается ситуация, когда точка «цэ» лежит внутри отрезка ![]() . Просто и естественно – криволинейную трапецию можно разделить на две части, т.е. изначальная площадь будет равна сумме площадей. Но данное свойство работает и в «нестандартном» случае, когда точка «цэ» лежит вне промежутка
. Просто и естественно – криволинейную трапецию можно разделить на две части, т.е. изначальная площадь будет равна сумме площадей. Но данное свойство работает и в «нестандартном» случае, когда точка «цэ» лежит вне промежутка ![]() . Желающие могут проанализировать это самостоятельно.
. Желающие могут проанализировать это самостоятельно.
Разумеется, формула работает и справа налево, таким образом, определённый интеграл можно как разделить на части, так и «склеить» из частей. Очень удобная вещь!
– Пожалуйста, запомните! Если подынтегральная функция ![]() , то
, то 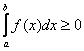 (здесь и далее полагаем, что
(здесь и далее полагаем, что ![]() ). И, наоборот, если
). И, наоборот, если ![]() , то интеграл будет неположительным:
, то интеграл будет неположительным: 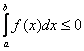 .
.
Свойство элементарно доказывается: снова вспоминаем, что 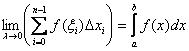 . Длины частичных промежутков положительны:
. Длины частичных промежутков положительны: ![]() , но в первом случае значения функции
, но в первом случае значения функции ![]() (криволинейная трапеция лежит не ниже оси абсцисс), а во втором случае
(криволинейная трапеция лежит не ниже оси абсцисс), а во втором случае ![]() (криволинейная трапеция лежит не выше оси абсцисс)
(криволинейная трапеция лежит не выше оси абсцисс)
Таким образом, если при вычислении интеграла ![]() у вас получилось отрицательное значение – ищите ошибку. Функция
у вас получилось отрицательное значение – ищите ошибку. Функция ![]() на промежутке интегрирования
на промежутке интегрирования ![]() (и, к слову, вообще на любом ненулевом промежутке), поэтому интеграл
(и, к слову, вообще на любом ненулевом промежутке), поэтому интеграл ![]() обязательно должен получиться положительным.
обязательно должен получиться положительным.
Наоборот – если интеграл 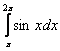 получился положительным, то здесь тоже где-то допущена ошибка, поскольку
получился положительным, то здесь тоже где-то допущена ошибка, поскольку ![]() на отрезке
на отрезке ![]() .
.
! Совет: перед решением любого определённого интеграла всегда полезно проанализировать знак подынтегральной функции!
– Ещё одно важное свойство. Если функции ![]() интегрируемы на
интегрируемы на ![]() , и для всех «икс» из данного промежутка справедливо неравенство
, и для всех «икс» из данного промежутка справедливо неравенство ![]() , то
, то
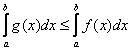
Тоже всё наглядно – график функции ![]() расположен не ниже графика функции
расположен не ниже графика функции ![]() , поэтому площадь
, поэтому площадь 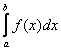 будет не меньше, а на практике почти всегда – больше площади
будет не меньше, а на практике почти всегда – больше площади 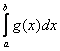 .
.
Из данного свойства следует важнейшая рабочая формула вычисления площади фигуры, ограниченной графиками функций ![]() и прямыми
и прямыми ![]() :
:
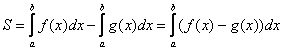
– Если ![]() на
на ![]() , то
, то 
Рассмотрим конкретную задачу, поясняющую геометрический смысл данного свойства, а то я чувствую, вы уже изнываете без практики =)
Пример 1
Оценить определенный интеграл ![]()
Решение: подынтегральная функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , а значит, достигает на нём
, а значит, достигает на нём ![]() и
и ![]() – наименьшего и наибольшего значений. Решаем стандартную двухшаговую задачу по нахождению
– наименьшего и наибольшего значений. Решаем стандартную двухшаговую задачу по нахождению ![]() :
:
1) Вычислим значения функции в критических точках, принадлежащих отрезку:
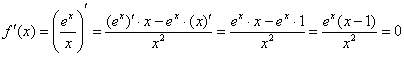
![]() – критическая точка.
– критическая точка.
![]()
2) Вычислим значения функции на концах отрезка:
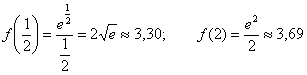
Таким образом: 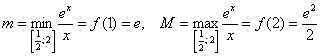
Длина отрезка интегрирования: ![]()
В результате, оценка определённого интеграла:

Ответ: 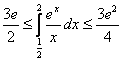
Геометрически это означает, что площадь ![]() криволинейной трапеции (синяя штриховка) не меньше площади красного прямоугольника
криволинейной трапеции (синяя штриховка) не меньше площади красного прямоугольника ![]() и не больше площади зелёного прямоугольника
и не больше площади зелёного прямоугольника ![]() :
:
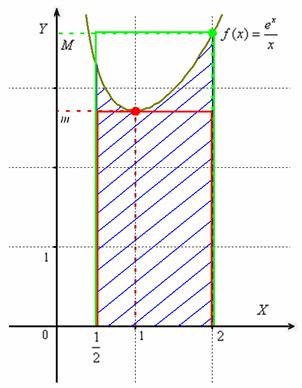
Да, оценка, конечно, очень грубая, но таково задание и оно иногда встречается в контрольных работах. Кстати, интеграл ![]() является неберущимся, и вычислить заштрихованную площадь можно лишь с определённой точностью, например, методом трапеций, по формуле Симпсона, с помощью разложения функции в ряд, др. способами.
является неберущимся, и вычислить заштрихованную площадь можно лишь с определённой точностью, например, методом трапеций, по формуле Симпсона, с помощью разложения функции в ряд, др. способами.
– И в заключение параграфа – теорема о среднем: если функция ![]() непрерывна на
непрерывна на ![]() , то существует точка
, то существует точка ![]() – такая, что
– такая, что 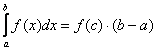 . Геометрический смысл теоремы я уже использовал при выводе формулы Ньютона-Лейбница, единственное, там речь шла о кусочке криволинейной трапеции, здесь же – о всей фигуре. Грубо говоря, всегда существует прямоугольник со стороной
. Геометрический смысл теоремы я уже использовал при выводе формулы Ньютона-Лейбница, единственное, там речь шла о кусочке криволинейной трапеции, здесь же – о всей фигуре. Грубо говоря, всегда существует прямоугольник со стороной ![]() (длина отрезка интегрирования), площадь которого равна площади
(длина отрезка интегрирования), площадь которого равна площади 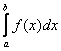 .
.
Доказательство опустим, поскольку в нём фигурируют другие теоремы математического анализа.
А сейчас оставшихся со мной читателей ждёт вознаграждение, позволяющее проникнуться, если хотите, философией темы:
Общая концепция задачи интегрирования
В предыдущих пунктах мы разобрали задачу нахождения площади, но это частная и довольно малая область применения интегрального исчисления. Существует великое множество задач интегрирования, при этом наибольшим разнообразием отличается даже не математика, а физика. Вернёмся к самому смыслу термина: интегрирование – это объединение. А объединить, как вы понимаете, можно много чего =) И в общем виде задача интегрирования ставится следующим образом, не судите строго, формулирую своими словами:
Требуется найти значение величины ![]() на отрезке
на отрезке ![]() . Величина
. Величина ![]() – это не обязательно площадь, объём либо какое-то другое геометрическое понятие. Это может быть что-нибудь с ярко выраженным физическим смыслом, например, работа силы. При этом известна производная величина, заданная функцией
– это не обязательно площадь, объём либо какое-то другое геометрическое понятие. Это может быть что-нибудь с ярко выраженным физическим смыслом, например, работа силы. При этом известна производная величина, заданная функцией ![]() на том же промежутке
на том же промежутке ![]() . Рассматриваемый отрезок и аргумент «тау» – тоже не обязательно геометрия, речь может идти, скажем, о временнОм промежутке и времени.
. Рассматриваемый отрезок и аргумент «тау» – тоже не обязательно геометрия, речь может идти, скажем, о временнОм промежутке и времени.
В предположении о непрерывности функции ![]() на
на ![]() , задача решается в два этапа:
, задача решается в два этапа:
Сначала рассматривается бесконечно малый отрезок ![]() промежутка
промежутка ![]() , на котором произведение
, на котором произведение ![]() равно бесконечно малому «кусочку»
равно бесконечно малому «кусочку» ![]() от разыскиваемого значения
от разыскиваемого значения ![]() . То есть, справедливо равенство
. То есть, справедливо равенство ![]() .
.
Далее проводится объединение (интегрирование) всех бесконечно малых элементов ![]() по отрезку
по отрезку ![]() , в результате чего и получается суммарное значение искомой величины:
, в результате чего и получается суммарное значение искомой величины: 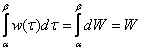 .
.
Примечание: в теории и практике вышеизложенные равенства почти всегда записывают в обратном порядке: 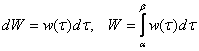 . Стандарты нарушены только для лучшего понимания материала.
. Стандарты нарушены только для лучшего понимания материала.
Давайте вспомним 1-й чертёж урока, где мы установили, что площадь ![]() криволинейной трапеции равна определённому интегралу
криволинейной трапеции равна определённому интегралу 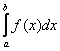 . Ведь что такое произведение
. Ведь что такое произведение ![]() ? Данное произведение выражает площадь прямоугольника с высотой
? Данное произведение выражает площадь прямоугольника с высотой ![]() и бесконечно малой длиной
и бесконечно малой длиной ![]() . Иными словами, это элементарный «кирпичик» площади:
. Иными словами, это элементарный «кирпичик» площади: ![]() .
.
Объединяя (интегрируя) эти бесконечно малые прямоугольники по отрезку ![]() , мы и получаем площадь всей криволинейной трапеции:
, мы и получаем площадь всей криволинейной трапеции: 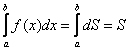 .
.
Заключительные примеры позволят вам ещё лучше понять сущность интегрирования:
Пример 2
Вычислить объём эллипсоида ![]()
Решение: перепишем уравнение эллипсоида в каноническом виде ![]() и выполним чертёж. Ввиду симметрии тела достаточно вычислить объём в 1-м октанте:
и выполним чертёж. Ввиду симметрии тела достаточно вычислить объём в 1-м октанте:
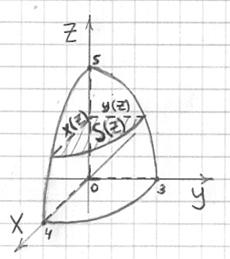
Прежде всего, обратим внимание на заштрихованную «площадку» ![]() – она представляет собой «четвертинку» эллипса с большой полуосью
– она представляет собой «четвертинку» эллипса с большой полуосью ![]() и малой полуосью
и малой полуосью ![]() , длины которых зависят от значения «зет». Сама площадь
, длины которых зависят от значения «зет». Сама площадь ![]() , разумеется, тоже величина переменная: мысленно положите сверху ладошку и начните опускать лифт вниз. Длины
, разумеется, тоже величина переменная: мысленно положите сверху ладошку и начните опускать лифт вниз. Длины ![]() , а вместе с ними и площадь
, а вместе с ними и площадь ![]() – начнут возрастать. Максимальные значения будет достигнуты в плоскости
– начнут возрастать. Максимальные значения будет достигнуты в плоскости ![]() :
: ![]() . В Примере № 2 урока о площади и объеме при параметрически заданной линии выведена формула площади эллипса
. В Примере № 2 урока о площади и объеме при параметрически заданной линии выведена формула площади эллипса ![]() . У нас же одна четверть эллипса, поэтому площадь «на нулевом этаже» будет составлять
. У нас же одна четверть эллипса, поэтому площадь «на нулевом этаже» будет составлять ![]()
Теперь поднимаем заштрихованную «площадку» ладошкой вверх – полуоси ![]() и площадь
и площадь ![]() будут уменьшаться – до тех пор, пока при
будут уменьшаться – до тех пор, пока при ![]() не выродятся в точку; площадь здесь станет нулевой:
не выродятся в точку; площадь здесь станет нулевой: ![]() .
.
В чём состоит трудность нахождения объёма ![]() данного тела? Трудность состоит в том, что стОит нам чуть-чуть «дёрнуться» и площадь эллипса изменится. Что делать? Использовать общий принцип интегрирования:
данного тела? Трудность состоит в том, что стОит нам чуть-чуть «дёрнуться» и площадь эллипса изменится. Что делать? Использовать общий принцип интегрирования:
На первом шаге рассматриваем «площадку» ![]() бесконечно малой толщины
бесконечно малой толщины ![]() . При этом произведение площади
. При этом произведение площади ![]() на высоту
на высоту ![]() будет равно элементарному, бесконечно малому элементу объема тела:
будет равно элементарному, бесконечно малому элементу объема тела: ![]() .
.
На втором шаге «плавно поднимаемся на лифте с 0-го на 5-й этаж», объединяя ВСЕ элементарные слои ![]() объёма:
объёма: 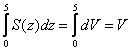 – получая тем самым итоговый объём тела.
– получая тем самым итоговый объём тела.
Суть разобрана, остальное – дело техники:
1) Найдём функцию ![]() длины большой полуоси эллипса. Для этого в уравнении эллипсоида
длины большой полуоси эллипса. Для этого в уравнении эллипсоида ![]() обнуляем «игрековую» координату:
обнуляем «игрековую» координату:
![]()
Поскольку дело происходит в 1-м октанте, то перед корнем будет знак «плюс»:
![]()
2) Аналогично находим функцию длины малой полуоси. В уравнении эллипсоида ![]() обнуляем «иксовую» координату и выражаем
обнуляем «иксовую» координату и выражаем ![]() :
:
![]()
3) Составим функцию площади ![]() , не забывая, что это «четвертинка» эллипса:
, не забывая, что это «четвертинка» эллипса:
![]()
И, наконец, «запускаем лифт», объединяя элементарные частички объёма ![]() :
:
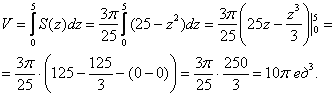
Так как рассматривалась только ![]() часть эллипсоида, результат умножаем на 8.
часть эллипсоида, результат умножаем на 8.
Ответ: ![]()
Если решить задачу с каноническим уравнением ![]() (в общем виде), то получится формула объема эллипсоида:
(в общем виде), то получится формула объема эллипсоида: ![]()
Следует отметить, что в общем случае эллипсоид не является телом вращения, поэтому к нему не применим «обычный» метод нахождения объема, изложенный в статье Объем тела вращения. Таким образом, разобранная задача оказывается не только поучительной, но ещё и крайне полезной. Желающие могут найти (Раздел IV Интегралы, Задача 20) ещё порядка 30 похожих примеров и потренироваться.
Для полноценной картины как нельзя кстати будет физика:
Пример 3
Найти путь, пройдённый телом в промежуток времени от ![]() до
до ![]() , если известен закон изменения его скорости
, если известен закон изменения его скорости ![]() (м/с)
(м/с)
Решение: обозначим через ![]() расстояние, пройдённое телом за 5 – 2 = 3 секунды – начиная с момента времени
расстояние, пройдённое телом за 5 – 2 = 3 секунды – начиная с момента времени ![]() и заканчивая моментом
и заканчивая моментом ![]() .
.
Немного проанализируем задачу. Вот если бы тело двигалось с постоянной скоростью, например, 7 м/с, то никаких проблем – оно бы за 3 секунды прошло путь в ![]() метр. Но у нас движение даже не равноускоренное (при котором ещё можно извернуться без матана) – у нас закон изменения скорости нелинейный. При этом в начальный момент времени скорость равна
метр. Но у нас движение даже не равноускоренное (при котором ещё можно извернуться без матана) – у нас закон изменения скорости нелинейный. При этом в начальный момент времени скорость равна ![]() м/с, а в конечный момент:
м/с, а в конечный момент: ![]() м/с. Но от этой информации легче не стало – какое расстояние
м/с. Но от этой информации легче не стало – какое расстояние ![]() успело пройти тело за эти три секунды?! Задание осложняется ещё и тем, что скорость существенно возрастает даже за малые промежутки времени, поэтому у нас нет и близкой оценки пройдённого пути.
успело пройти тело за эти три секунды?! Задание осложняется ещё и тем, что скорость существенно возрастает даже за малые промежутки времени, поэтому у нас нет и близкой оценки пройдённого пути.
Как быть? На помощь приходит интегрирование. Рассмотрим бесконечно малый промежуток времени ![]() , на котором скорость тела можно считать постоянной (или, как говорят физики, мгновенной). Тогда произведение данной скорости на промежуток времени
, на котором скорость тела можно считать постоянной (или, как говорят физики, мгновенной). Тогда произведение данной скорости на промежуток времени ![]() равно элементарному бесконечно малому «кусочку» пройдённого пути:
равно элементарному бесконечно малому «кусочку» пройдённого пути: ![]() (скорость умножить на время – это же расстояние, верно?).
(скорость умножить на время – это же расстояние, верно?).
Всё что осталось сделать – это объединить микроскопические «шажочки» ![]() на временнОм промежутке
на временнОм промежутке ![]() :
:
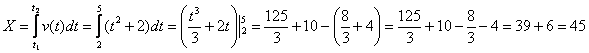
Ответ: 45 метров
Ну а у меня такое впечатление, что эту статью я создавал 45 лет =) …хотя вроде бы она не самая большая, да и чертежи быстро сделал… Наверное по той причине, что довольно долго обдумывал, что включить в содержание, а что оставить за кадром. Так или иначе, думаю, что отобранная информация значительно повысила ваш уровень понимания темы.
Желаю успехов!
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright