Области на комплексной плоскости

Ехали медведи, на велосипеде,
А за ними области, на комплексной плоскости.

После курса молодого ТФКП-ниста, рассмотрим материал, важный для изучения всего комплексного анализа. Сначала будет немного терминов и теории, затем практика, где мы научимся распознавать и строить различные области на комплексной плоскости.

И в первом же абзаце нам встретились строгие понятия. Комплексная плоскость – это геометрическое представление множества комплексных чисел:

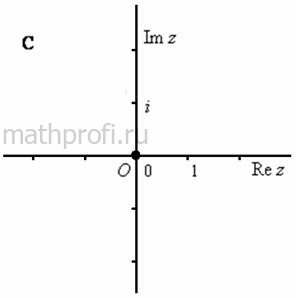
Если к множеству присоединить бесконечно удалённую точку , то говорят о расширенной комплексной плоскости, которую иногда обозначают . Пожалуйста, различайте эти термины и виды плоскостей.

Окрестностью точки называют круг произвольного радиуса . При этом под кругом подразумевается открытый круг – без его границы (окружности). Внешняя часть этого круга (точки за пределами границы) образует окрестность бесконечно удалённой точки:

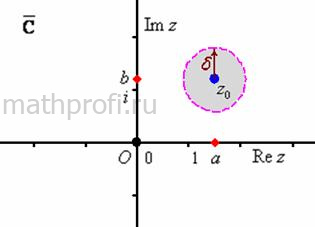
И вообще, под областью в комплексном анализе «по умолчанию» понимают, как правило, открытую область – без учёта её границы. Всегда имейте в виду этот факт.

Дадим строгие определения области и её границы.

Точку называют внутренней точкой области , если существует её окрестность (пусть очень малая), такая, что ВСЕ точки этой окрестности принадлежат области . Область – это множество её внутренних точек, причём, любые две точки этого множества можно соединить гладкой или кусочно-гладкой* линией, полностью состоящей из внутренних точек.

* Линию называют гладкой, если в любой её точке можно провести касательную (существует конечная производная). Кусочно-гладкая линия состоит из фрагментов («кусков») гладких линий, последовательно соединённых между собой, простейший пример – ломаная.

Из определения следует, что два непересекающихся круга (например) или даже два соприкасающихся круга – единой области не образуют. А вот следующее множество точек– да, для удобства область я изобразил в 1-й координатной четверти:

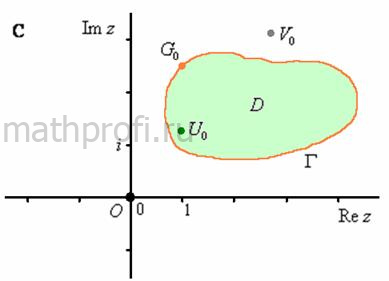
…Рука почти не дрогнула, но до Рубенса, конечно, далековато :)

Точка называется граничной точкой области, если в ЛЮБОЙ её окрестности есть точки КАК принадлежащие этой области, так и НЕ принадлежащие ей. Множество граничных точек области называют границей данной области. В данном примере это оранжевая линия («гамма большое», можно просто «гэ»).

Под замкнутой областью понимают саму область + её границу, такую область обозначают с чёрточкой наверху: .

Точка называется внешней точкой области , если существует её окрестность (пусть очень малая), ВСЕ точки которой НЕ принадлежат области .

Следует заметить, что линия на рисунке выше делит комплексную плоскость на ДВЕ области: область и её внешнюю часть, причём, обе области имеют одну и ту же границу. Обратите внимание, что точка является внутренней точкой «внешней» области по определению.

И ещё одно важное понятие – связность области.

Комплексную область называют односвязной, если (вдумываемся!) ЛЮБАЯ замкнутая линия, лежащая внутри неё, содержит внутри себя лишь точки данной области. Или в эквивалентной топологической формулировке: если любую замкнутую линию, лежащую внутри области можно непрерывно стянуть в точку, не выходя за пределы этой области.

В частности, односвязна область, которая ограничена одной замкнутой линией без самопересечений. Пример такой области приведён на рисунке выше: какой бы замкнутый «путь» в области мы ни выбрали, внутри него (соответствующей линии) – ВСЕ точки будут принадлежать области .

Но бывают и другие ситуации:

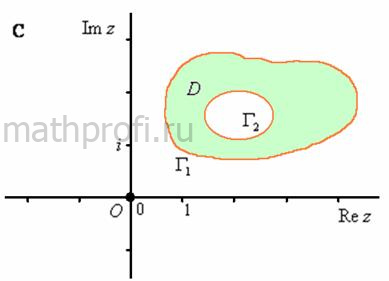
Здесь область ограничена двумя замкнутыми линиями , которые не пересекаются, и такая область является двусвязной. В ней мы можем выбрать замкнутый маршрут, внутри которого далеко не все точки будут принадлежать области (любой замкнутый путь вокруг ). При этом линия может быть вырождена в дугу непрерывной линии или даже в единственную точку, не принадлежащую области .

Требование непересечения линий – критично. Так, если касается в одной точке, то область становится односвязной. Если же касания два, то получатся две разные области.

Аналогично определяются трёх- четырёх- и так далее связные области. В частности, четырёхсвязная область имеет четыре непересекающиеся граничные линии. В примере ниже одна из таких линий представляет собой точку:

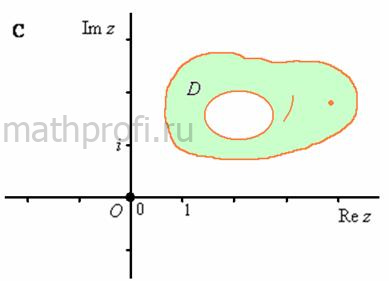
Грубо говоря, связность области можно определить по количеству внутренних «дырок»: у двусвязной области она одна, и трехсвязной – две, у четырёхсвязной – три и так далее.

С теорией уложились бодренько, теперь практика.

Как задать область на комплексной плоскости?

Можно графически (чем я только что занимался), но лучше – аналитически, с помощью неравенств. Начнём с простейших примеров:

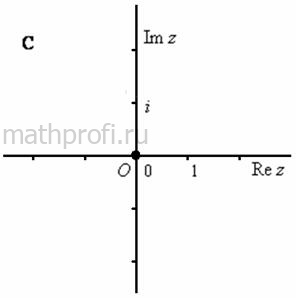
Неравенству соответствуют те комплексные числа, действительная часть которых больше нуля, поэтому оно определяет правую полуплоскость (штриховать уж не буду). Если неравенство нестрогое , то к области следует добавить ось . Соответственно, неравенство задаёт левую полуплоскость, а – её же вместе с мнимой осью.

Аналогично, неравенству удовлетворяют те комплексные «зет», мнимая часть которых больше нуля, поэтому сие неравенство определяет верхнюю полуплоскость, а неравенство – дополнительно ось . Неравенству соответствует нижняя полуплоскость и неравенству – она же вместе с действительной осью.

Рассмотрим более содержательные примеры:

Пример 1

Построить области, заданные неравенствами:

а) ;
б) .

Дополнительно обозначим оси привычным «иксом» и «игреком» и решаем.

а) Двойному неравенству соответствуют те комплексные «зет», действительная часть которых не меньше «минус» единицы и меньше двух. Этому условию соответствуют все числа из полосы, ограниченной прямыми , при этом прямая принадлежит искомой области (серая штриховка на рис. ниже).

б) Неравенству удовлетворяют все числа, мнимая часть которых больше нуля и не больше . Соответствующая область представляет собой полосу между прямыми , при этом прямая принадлежит области, а действительная ось – нет (голубой цвет):

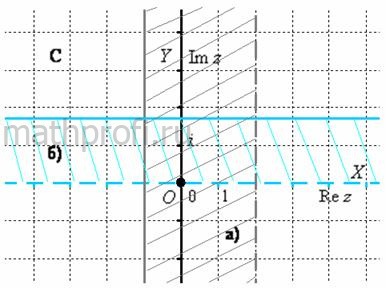
При выполнении чертежа от руки во многих случаях оптимален следующий масштаб:
1 ед. = 2 тетрадные клетки (1 см).

Занятное задание для самостоятельного решения:

Пример 2

Изобразить на комплексной плоскости множество точек, удовлетворяющее следующим условиям:

а) ;
б) .

Здесь в каждом пункте подразумевается одновременное выполнение обоих условий, и более точно их следует записать в форме системы: а) , б) . На практике вам может встретиться и тот и другой вариант.

Выполняем чертежи от руки (хотя бы схематически!), сверяемся с решением в конце урока и продолжаем:

Пример 3

Изобразить следующие области:

а) ;
б) .

Решение: а) Давайте вдумаемся в это неравенство: – ему удовлетворяют все числа, модуль которых меньше единицы. А это числа из круга с центром в начале координат радиуса 1 (серая штриховка на чертеже ниже).

И вообще, неравенство задаёт круг с центром в начале координат радиуса . Если неравенство нестрогое , то к кругу следует добавить его границу, то бишь окружность (которая, к слову, определяется уравнением ).

Неравенство же определяют внешнюю часть этого замкнутого круга (всю оставшуюся плоскость – окромя круга с его границей). В нашем конкретном примере – это вся комплексная плоскость, кроме замкнутого единичного круга с центром в начале координат.

И пункт б) я начну с общего случая. Неравенство определяет круг с центром в точке радиуса . Это можно запомнить формально. Но давайте опять же вникнем в смысл. Как и в действительном случае (см. самый низ), модуль разности означает расстояние между числами. Таким образом, число отстоИт от числа меньше, чем на , а этому условию как раз и удовлетворяет любая точка указанного выше круга. Аналогично предыдущему пункту, неравенство определяет соответствующий замкнутый круг, а неравенство – его внешнюю часть.

Теперь вернёмся к конкретному неравенству и представим его в виде (внимание!):

– замкнутый круг с центром в точке (малиновый цвет):

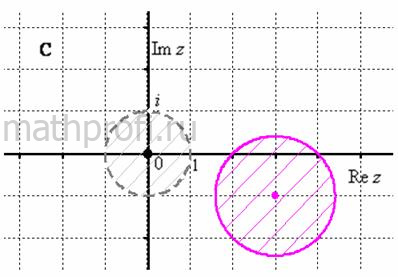
При выполнении чертежа от руки строго рекомендую циркуль, при этом его остриё нежелательно отрывать от бумаги, пока не прочертите всю окружность.

Следующее задание для самостоятельного решения:

Пример 4

Изобразить на комплексной плоскости область, ограниченную линиями , .

Не ленимся – рисуем, и факультативное неравенство – рассуждаем:

Пример 5

Изобразить область, соответствующую неравенству
На первом шаге используйте свойство модуля .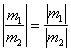
После чего нас ждёт ещё одна важная фигура:

Пример 6

Изобразить область, соответствующую условию .

Решение: двойное неравенство вида можно записать в виде системы:

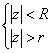
Первое условие определят круг с центром в начале координат радиуса , второе условие (представляем в уме!) – внешнюю часть замкнутого круга с тем же центром, но меньшего радиуса . И коль скоро это система, то её решением будет общая часть (пересечение) этих областей.

Таким образом, двойное неравенство вида определяет кольцо с центром в начале координат, внутреннего радиуса и внешнего радиуса .

Наш случай элементарен:

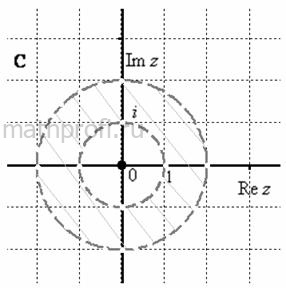
Заметьте, что кольцо – это двусвязная область.

Если одно или оба неравенства нестрогие, то к области следуют добавить соответствующую окружность или обе.

И по аналогии с предыдущими примерами, неравенству соответствует кольцо с центром в точке , внутреннего радиуса , внешнего радиуса . Этот случай для самостоятельного потребления, с приправой, чтобы не было так пресно:

Пример 7

Изобразить на комплексной плоскости область, удовлетворяющую условиям , .

…Посидите, подумайте, какие числа удовлетворяю первому условию…. Да, и старайтесь не пренебрегать учебными задачами, в них я часто комментирую важные детали, которые не вошли в «основной текст».

И в заключение урока за аргумент замолвим слово:

Пример 8

Изобразить на комплексной плоскости область, удовлетворяющую условию

И решение очень простое: этому условию соответствуют те комплексные числа, аргумент которых больше , но меньше . Геометрически – это соответствующий фрагмент плоскости между лучами и :

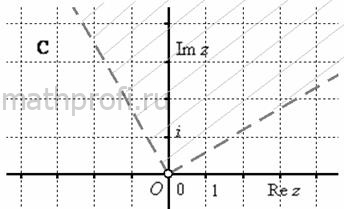
При выполнении чертежа от руки используйте транспортир, а если позабылись углы – справку по тригонометрии.

Если одно из неравенств или оба – нестрогие, то соответствующие лучи следует добавить к области и изобразить непрерывной линией. Однако начало координат в любом случае в область не войдёт (т. к. для него аргумент не определён), а посему эта точка должна быть «выколота».

Если же дано неравенство вида , то углы следует отмерять не от начала координат, а от точки , и лучи тоже откладывать от неё. Сама же точка при любых раскладах в область не войдёт. С геометрией этого случая разберитесь самостоятельно, и простенькое задание для тренировки:

Пример 9

Найти множество точек, удовлетворяющее условиям , .

Решаем! ;)

В некоторых задачах неравенство для аргумента может быть «одинарное», например, или . Но самом деле оно двойное. Учитывая, что главное значение аргумента изменяется в пределах , имеем области:
и соответственно

Далее разберём…, пожалуй, линии на комплексной плоскости, некоторые из которых мы уже вовсю начали использовать.

Желаю успехов!

Решения и ответы:

Пример 2. Решение: а) Искомая область ограничена прямыми снизу и сверху соответственно и прямой справа, причём последняя области не принадлежит (серая штриховка на чертеже).

б) Данная область представляет собой квадрат, ограниченный прямыми и , при этом прямые и не принадлежат области (зелёный цвет на чертеже):

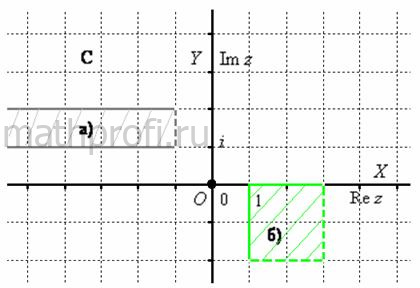
Примечание: обратите внимание, что угловые точки, соответствующие строгим неравенствам, не принадлежат областям («выколоты»).

Пример 4. Решение: Неравенству соответствует внешняя часть круга с центром в начале координат радиуса 3.
Преобразуем второе неравенство: – круг с центром в точке радиуса 1,5.

Искомая область представляет собой пересечение этих двух областей («полумесяц»):

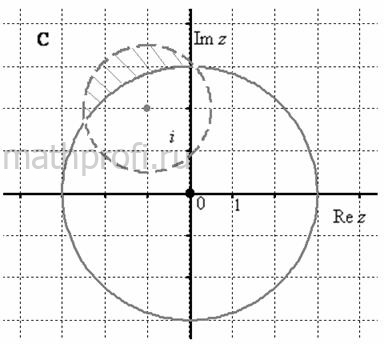
Примечание: опять же обратите внимание, что точки пересечения окружностей не входят в область (по причине строгости второго неравенства).

Пример 5. Решение: используем свойство модуля: .
Умножим обе части неравенства на , имея в виду, что :

Сначала удобно разобраться с равенством . Условию соответствуют значения , равноудалённые от точек . В нашем случае – это точки, которые равноудалены от точек , а это точки, лежащие на оси .
Неравенству же соответствуют ТАКИЕ точки «зет», у которых расстояние до точки меньше расстояния до точки , а это точки правой полуплоскости .
Таким образом, нестрогому неравенству соответствует правая полуплоскость, включая ось :

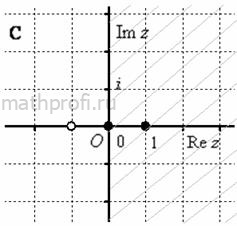
Примечание: соответственно, неравенству удовлетворяют точки левой полуплоскости (без мнимой оси), исключая точку . Однако если изначально дано неравенство , то эту точку следует добавить к решению.

Пример 7. Решение: естественным образом присоединим к комплексной плоскости декартову систему координат . Условию , очевидно, соответствуют точки прямой , а неравенству («икс больше игрек») – все точки ниже этой прямой.
Преобразуем двойное неравенство:
– ему соответствует кольцо с центром в точке , внутреннего радиуса , внешнего радиуса , при этом внутренняя окружность входит в область.

Искомая область представляет собой пересечение выявленных выше областей:

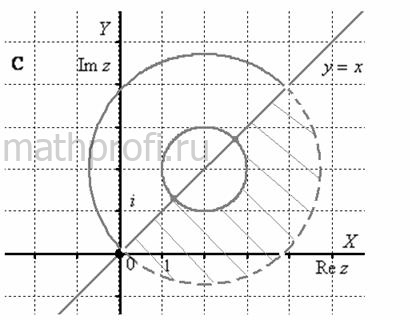
Примечание: точки пересечения прямой с внутренней окружностью в область входят, а с внешней окружностью – нет.

Пример 9. Решение: представим первое неравенство в виде :
– замкнутый круг с центром в точке радиуса .
Представим второе неравенство в виде :
– часть плоскости, полученная поворотом луча, исходящего из точки , от угла (относительно положительной полуоси ) до , при этом первый граничный луч в область не входит, а второй – входит:

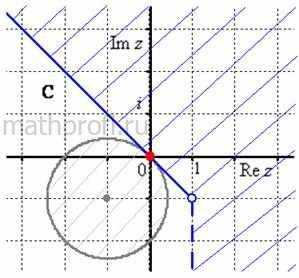
Из чертежа следует, что сразу обоим условиям удовлетворяет единственная точка – это точка касания окружности второго граничного луча.

Ответ:

Следует добавить, что искомое множество точек может быть и пустым – если области не пересекаются. В только что разобранном примере для этого достаточно строгости неравенств первого и / или второго условия.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?