

 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Предел функции двух переменных.
Понятие и примеры решений
Добро пожаловать на третий урок по теме ФНП, где наконец-то начали сбываться все ваши опасения =) Как многие подозревали, понятие предела распространяется и на функцию ![]() произвольного количества аргументов, в чём нам сегодня и предстоит разобраться. Однако есть оптимистичная новость. Она состоит в том, что при
произвольного количества аргументов, в чём нам сегодня и предстоит разобраться. Однако есть оптимистичная новость. Она состоит в том, что при ![]() предел в известной степени абстрактен и соответствующие задания крайне редко встречаются на практике. В этой связи наше внимание будет сосредоточено на пределах функции
предел в известной степени абстрактен и соответствующие задания крайне редко встречаются на практике. В этой связи наше внимание будет сосредоточено на пределах функции ![]() двух переменных или, как мы чаще её записываем:
двух переменных или, как мы чаще её записываем: ![]() .
.
Многие идеи, принципы и методы схожи с теорией и практикой «обычных» пределов, а значит, на данный момент вы должны уметь находить пределы и самое главное ПОНИМАТЬ, что такое предел функции одной переменной. И, коль скоро судьба привела вас на эту страничку, то, скорее всего, уже немало понимаете-умеете. А если и нет – ничего страшного, все пробелы реально заполнить в считанные часы и даже минуты.
События этого занятия разворачиваются в нашем трёхмерном мире, и поэтому будет просто огромным упущением не принять в них живое участие. Сначала соорудим хорошо известную декартову систему координат в пространстве. Давайте встанем и немного походим по комнате… …пол, по которому вы ходите – это плоскость ![]() . Поставим где-нибудь ось
. Поставим где-нибудь ось ![]() … ну, например, в любом углу, чтобы не мешалась на пути. Отлично. Теперь, пожалуйста, посмотрите вверх и представьте, что там зависло расправленное одеяло. Это поверхность, заданная функцией
… ну, например, в любом углу, чтобы не мешалась на пути. Отлично. Теперь, пожалуйста, посмотрите вверх и представьте, что там зависло расправленное одеяло. Это поверхность, заданная функцией ![]() . Наше перемещение по полу, как нетрудно понять, имитирует изменение независимых переменных
. Наше перемещение по полу, как нетрудно понять, имитирует изменение независимых переменных ![]() , и мы можем передвигаться исключительно под одеялом, т. е. в области определения функции двух переменных. Но самое интересное только начинается. Прямо над кончиком вашего носа по одеялу ползает маленький тараканчик, куда вы – туда и он. Назовём его Фредди. Его перемещение имитирует изменение соответствующих значений
, и мы можем передвигаться исключительно под одеялом, т. е. в области определения функции двух переменных. Но самое интересное только начинается. Прямо над кончиком вашего носа по одеялу ползает маленький тараканчик, куда вы – туда и он. Назовём его Фредди. Его перемещение имитирует изменение соответствующих значений ![]() функции (за исключением тех случаев, когда поверхность либо её фрагменты параллельны плоскости
функции (за исключением тех случаев, когда поверхность либо её фрагменты параллельны плоскости ![]() и высота не меняется). Уважаемый читатель с именем Фредди, не обижайся, так надо для науки.
и высота не меняется). Уважаемый читатель с именем Фредди, не обижайся, так надо для науки.
Возьмём в руки шило и проткнём одеяло в произвольной точке, высоту которой обозначим через ![]() , после чего строго под отверстием воткнём инструмент в пол – это будет точка
, после чего строго под отверстием воткнём инструмент в пол – это будет точка ![]() . Теперь начинаем бесконечно близко приближаться к данной точке
. Теперь начинаем бесконечно близко приближаться к данной точке ![]() , причём приближаться мы имеем право ПО ЛЮБОЙ траектории (каждая точка которой, разумеется, входит в область определения). Если ВО ВСЕХ случаях Фредди будет бесконечно близко подползать к проколу на высоту
, причём приближаться мы имеем право ПО ЛЮБОЙ траектории (каждая точка которой, разумеется, входит в область определения). Если ВО ВСЕХ случаях Фредди будет бесконечно близко подползать к проколу на высоту ![]() и ИМЕННО НА ЭТУ ВЫСОТУ, то функция
и ИМЕННО НА ЭТУ ВЫСОТУ, то функция ![]() имеет предел в точке
имеет предел в точке ![]() при
при ![]() :
:
![]()
Если при указанных условиях проколотая точка расположена на краю одеяла, то предел всё равно будет существовать – важно, чтобы в сколь угодно малой окрестности острия шила были хоть какие-то точки из области определения функции. Кроме того, как и в случае с пределом функции одной переменной, не имеет значения, определена ли функция ![]() в точке
в точке ![]() или нет. То есть наш прокол можно залепить жвачкой (считать, что функция двух переменных непрерывна) и это не повлияет на ситуацию – вспоминаем, что сама суть предела подразумевает бесконечно близкое приближение, а не «точный заход» в точку.
или нет. То есть наш прокол можно залепить жвачкой (считать, что функция двух переменных непрерывна) и это не повлияет на ситуацию – вспоминаем, что сама суть предела подразумевает бесконечно близкое приближение, а не «точный заход» в точку.
Однако безоблачная жизнь омрачается тем фактом, что в отличие от своего младшего брата, предел ![]() гораздо более часто не существует. Это связано с тем, что к той или иной точке на плоскости
гораздо более часто не существует. Это связано с тем, что к той или иной точке на плоскости ![]() обычно существует очень много путей, и каждый из них должен приводить Фредди строго к проколу (опционально «залепленному жвачкой») и строго на высоту
обычно существует очень много путей, и каждый из них должен приводить Фредди строго к проколу (опционально «залепленному жвачкой») и строго на высоту ![]() . А причудливых поверхностей с не менее причудливыми разрывами хоть отбавляй, что приводит к нарушению этого жёсткого условия в некоторых точках.
. А причудливых поверхностей с не менее причудливыми разрывами хоть отбавляй, что приводит к нарушению этого жёсткого условия в некоторых точках.
Организуем простейший пример – возьмём в руки нож и разрежем одеяло таким образом, чтобы проколотая точка лежала на линии разреза. Заметьте, что предел ![]() всё ещё существует, единственное, мы потеряли право ступать в точки под линией разреза, так как этот участок «выпал» из области определения функции. Теперь аккуратно приподнимем левую часть одеяла вдоль оси
всё ещё существует, единственное, мы потеряли право ступать в точки под линией разреза, так как этот участок «выпал» из области определения функции. Теперь аккуратно приподнимем левую часть одеяла вдоль оси ![]() , а правую его часть, наоборот – сдвинем вниз или даже оставим её на месте. Что изменилось? А принципиально изменилось следующее: если сейчас мы будем подходить к точке
, а правую его часть, наоборот – сдвинем вниз или даже оставим её на месте. Что изменилось? А принципиально изменилось следующее: если сейчас мы будем подходить к точке ![]() слева, то Фредди окажется на бОльшей высоте, чем, если бы мы приближались к данной точке справа. Таким образом, предела
слева, то Фредди окажется на бОльшей высоте, чем, если бы мы приближались к данной точке справа. Таким образом, предела ![]() не существует.
не существует.
Рассмотрим фрагмент плоскости ![]() :
:
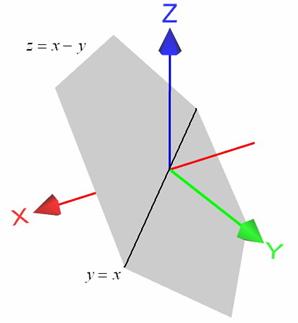
Очевидно, что предел функции ![]() существует в любой конечной точке
существует в любой конечной точке ![]() плоскости
плоскости ![]() и первый практический приём решения точно такой же:
и первый практический приём решения точно такой же:
сначала пытаемся выполнить прямую подстановку значений 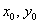
Например:
![]() и т. п.
и т. п.
Неопределённостей нет и пределы вычислены! Более того, если любую точку плоскости ![]() «выколоть шилом», то предел там всё равно будет существовать, но в подобных случаях как раз и появляется неопределённость.
«выколоть шилом», то предел там всё равно будет существовать, но в подобных случаях как раз и появляется неопределённость.
К слову, о неопределённостях. Отличительная особенность пределов функций нескольких переменных состоит в том, что ЗА КАЖУЩЕЙСЯ неопределённостью частенько скрывается несуществование предела, пожалуйста:
![]()
Что здесь? Неопределённость ![]() ? Или может быть предел равен нулю? …На самом деле данного предела не существует и тому есть очень простое геометрическое объяснение. Давайте посмотрим на два ближних к нам октанта (
? Или может быть предел равен нулю? …На самом деле данного предела не существует и тому есть очень простое геометрическое объяснение. Давайте посмотрим на два ближних к нам октанта (![]() ),в которых плоскость
),в которых плоскость ![]() пересекает координатную плоскость
пересекает координатную плоскость ![]() по прямой
по прямой ![]() и располагается как в верхнем, так и нижнем полупространстве. Таким образом, если мы будем уходить по обеим переменным на «плюс бесконечность», то Фредди может приближаться по «серой» поверхности, как к «плюс», так и к «минус бесконечности», а также ползти по прямой
и располагается как в верхнем, так и нижнем полупространстве. Таким образом, если мы будем уходить по обеим переменным на «плюс бесконечность», то Фредди может приближаться по «серой» поверхности, как к «плюс», так и к «минус бесконечности», а также ползти по прямой ![]() на нулевой высоте. Или вообще петлять туда-сюда – это зависит от нашего маршрута в плоскости
на нулевой высоте. Или вообще петлять туда-сюда – это зависит от нашего маршрута в плоскости ![]() . Следовательно, с пределом
. Следовательно, с пределом ![]() дела плохи.
дела плохи.
По той же причине, не существует и предела ![]() (два дальних от нас октанта).
(два дальних от нас октанта).
А вот с пределом ![]() всё отлично – при
всё отлично – при ![]() поверхность
поверхность ![]() расположена выше плоскости
расположена выше плоскости ![]() (левый верхний октант) и нигде не ограничена сверху, поэтому при
(левый верхний октант) и нигде не ограничена сверху, поэтому при ![]() Фредди по-любому уползёт на «плюс бесконечность». Собственно, это легко показать и аналитически:
Фредди по-любому уползёт на «плюс бесконечность». Собственно, это легко показать и аналитически:
![]()
«Зеркальный» предел ![]() проанализируйте самостоятельно.
проанализируйте самостоятельно.
…Как же всё таки удобно говорить «Фредди» вместо «соответствующие значения функции» =)
Пожалуйста, «сфотографируйте» другие типовые примеры, в которых неопределённость лишь КАЖЕТСЯ, но в действительности же пределов не существует:
![]()
И на всякий случай отмечу, что перечисленные функции сами по себе не являются какими-то «прокажёнными», то есть во многих других точках с пределами полный порядок, например: ![]() и т. д.
и т. д.
Строгое определение предела функции двух переменных даётся по аналогии определения предела функции одной переменной. Подход Эдуарда Гейне заключается в рассмотрении последовательностей точек ![]() , стремящихся к
, стремящихся к ![]() , и соответствующих последовательностей значений функций
, и соответствующих последовательностей значений функций ![]() , стремящихся к
, стремящихся к ![]() . Предел по Коши определяется всё теми же окрестностями, но в пространственном случае за
. Предел по Коши определяется всё теми же окрестностями, но в пространственном случае за ![]() -окрестность обычно выбирают круг либо прямоугольник с центром в точке
-окрестность обычно выбирают круг либо прямоугольник с центром в точке ![]() , а
, а ![]() -окрестность представляет собой целый «слой», заключенный между плоскостями
-окрестность представляет собой целый «слой», заключенный между плоскостями ![]() . Точные формулировки можно найти, например, у Бохана либо Фихтенгольца, и если вы усвоили минимальные теоретические сведения о пределах, то никаких трудностей возникнуть не должно. Более обстоятельный материал есть в учебнике Ильина/Садовничего и К, где детально рассматривается в том числе и обобщенный случай предела функции в
. Точные формулировки можно найти, например, у Бохана либо Фихтенгольца, и если вы усвоили минимальные теоретические сведения о пределах, то никаких трудностей возникнуть не должно. Более обстоятельный материал есть в учебнике Ильина/Садовничего и К, где детально рассматривается в том числе и обобщенный случай предела функции в ![]() пространстве. Кстати, не надо слишком сильно смеяться над моими тараканами – во время путешествия под одеялом я рассказал вам побольше, чем типовой кирпич по математическому анализу ;-) Но всё это, конечно, было в описательном плане – исключительно для понимания. Хотя определение предела по Гейне в такой интерпретации выглядит действительно смешно =)
пространстве. Кстати, не надо слишком сильно смеяться над моими тараканами – во время путешествия под одеялом я рассказал вам побольше, чем типовой кирпич по математическому анализу ;-) Но всё это, конечно, было в описательном плане – исключительно для понимания. Хотя определение предела по Гейне в такой интерпретации выглядит действительно смешно =)
Ну а сейчас мы переходим к обширному практическому материалу, и первые примеры будут посвящены заигранным баянам, которые встречаются не только на практике, но и в учебной литературе:
Пример 1
Найти предел функции
![]()
После прямой подстановки значений ![]() в выражение под значком предела получается подлежащая ликвидации неопределённость
в выражение под значком предела получается подлежащая ликвидации неопределённость ![]() . Прежде всего, обратим внимание, что поверхность
. Прежде всего, обратим внимание, что поверхность ![]() терпит разрыв в единственной точке. И действительно, равенство
терпит разрыв в единственной точке. И действительно, равенство ![]() выполняется только в начале координат. Но существует ли там предел?
выполняется только в начале координат. Но существует ли там предел?
Проведём небольшое исследование. Сначала начнём приближаться к точке ![]() по оси абсцисс
по оси абсцисс ![]() (синяя стрелка).
(синяя стрелка).
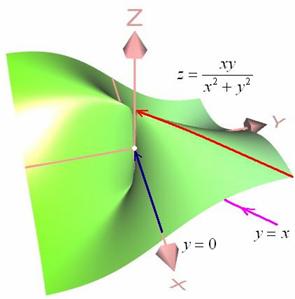
На схематическом чертеже хорошо видно, что соответствующие значения функции приближаются к нулю – ведь поверхность явно проходит через ось ![]() . Но иногда явное оказывается вовсе не явным ;-), и возникает вопрос: как в этом удостовериться аналитически? Очень просто – подставим в функцию
. Но иногда явное оказывается вовсе не явным ;-), и возникает вопрос: как в этом удостовериться аналитически? Очень просто – подставим в функцию ![]() и вычислим предел по данному пути:
и вычислим предел по данному пути:
![]() – обратите внимание, что никакой неопределённости тут нет: ноль, делённый на бесконечно малое число, равен осязаемому и железобетонному нулю.
– обратите внимание, что никакой неопределённости тут нет: ноль, делённый на бесконечно малое число, равен осязаемому и железобетонному нулю.
Теперь будем приближаться к началу координат по прямой ![]() (малиновая линия) и выясним, куда же приползёт Фредди. Судя по чертежу, куда-то выше (красная стрелка), хотя опять же не факт – вдруг там поверхность «ныряет» к нулю? Вычислим предел в предположении, что
(малиновая линия) и выясним, куда же приползёт Фредди. Судя по чертежу, куда-то выше (красная стрелка), хотя опять же не факт – вдруг там поверхность «ныряет» к нулю? Вычислим предел в предположении, что ![]() :
:
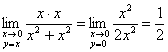
В результате получены разные числа, что противоречит определению предела, согласно которому ЛЮБОЙ допустимый маршрут к точке ![]() должен приводить Фредди к какому-то одному значению
должен приводить Фредди к какому-то одному значению ![]() . Таким образом, данного предела не существует. Вблизи точки разрыва поверхность бесконечно близко приближается («стягивается») к оси
. Таким образом, данного предела не существует. Вблизи точки разрыва поверхность бесконечно близко приближается («стягивается») к оси ![]() на различных высотах.
на различных высотах.
Но с этим примером нам повезло – совершено понятно, что в общем случае различные прямые можно перебирать до бесконечности и поэтому рациональнее проверить сразу весь «пучок» ![]() . Это множество вкупе с уравнением оси ординат
. Это множество вкупе с уравнением оси ординат ![]() учитывает все прямые пути подхода к началу координат. Оформляем решение:
учитывает все прямые пути подхода к началу координат. Оформляем решение:
![]()
Проведём замену ![]()
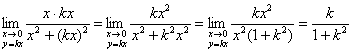
Результат зависит от коэффициента ![]() , следовательно, данного предела не существует.
, следовательно, данного предела не существует.
Готово!
Подставляя конкретные значения углового коэффициента, можно вычислить, на какой высоте Фредди будет приближаться к оси аппликат, если мы будем подходить к началу координат по той или иной прямой. В коварном случае потребуется дополнительно исследовать уравнение ![]() (которое не входит в семейство
(которое не входит в семейство ![]() ) но здесь до этого просто не дошло дело.
) но здесь до этого просто не дошло дело.
! Внимание! Иногда встречаются задачи, в которых требуется вычислить предел ТОЛЬКО по какой-либо линии, и, повторю очевидный факт: несмотря на отсутствие общего предела, предел по какому-либо частному направлению может себе преспокойно существовать. Например:
вычислим предел ![]() по прямой
по прямой ![]() :
:
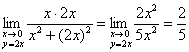 ;
;
теперь выясним, чему равен тот же предел, если приближаться к началу координат по параболе ![]() :
:
 и т. д.
и т. д.
Однако по многим маршрутам не существует даже и частного предела. Например, если мы приближаемся к нулю по «петляющей» траектории.
И из вышесказанного легко понять серьёзный недостаток рассмотренного метода решения: строго говоря, он пригоден лишь для обоснования НЕСУЩЕСТВОВАНИЯ предела. Ведь если мы выясним, что Фредди попадает на одну и ту же высоту ![]() по любой прямой, то этого ещё не достаточно. Согласно определению предела, нужно показать, что такой же результат получится и при ЛЮБОМ ДРУГОМ способе подхода к предельной точке. Этот вопрос решается с помощью перехода к полярным координатам.
по любой прямой, то этого ещё не достаточно. Согласно определению предела, нужно показать, что такой же результат получится и при ЛЮБОМ ДРУГОМ способе подхода к предельной точке. Этот вопрос решается с помощью перехода к полярным координатам.
![]()
Перейдём к полярной системе координат:
![]()
Предельная точка ![]() – есть начало координат, а посему:
– есть начало координат, а посему:
![]() , как оно чаще всего и бывает в подобных задачах.
, как оно чаще всего и бывает в подобных задачах.
Если ![]() , то полярному радиусу ничего не остаётся, как тоже стремиться к нулю:
, то полярному радиусу ничего не остаётся, как тоже стремиться к нулю: ![]() , что совершенно естественно.
, что совершенно естественно.
![]()
Результат зависит от «угла атаки», следовательно, предела не существует.
Но не всё так просто:
Пример 2
Найти предел функции
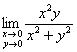
Предложенная функция тоже терпит разрыв в начале координат, и предел может, как существовать, так и не существовать.
Как лучше решать подобные пределы? С моей точки зрения, выгодно придерживаться следующей тактики: сначала на черновике быстренько исследуем все прямые пути:
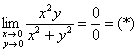
Проведём замену: ![]()
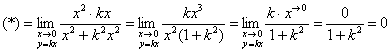
Предел не зависит от углового коэффициента прямой, по которой мы приближаемся к точке ![]() . Но расслабляться ещё рано! Не забываем, что в пучок прямых
. Но расслабляться ещё рано! Не забываем, что в пучок прямых ![]() не входит ось ординат! И поэтому уравнение
не входит ось ординат! И поэтому уравнение ![]() подлежит отдельному исследованию. Проще всего подставить данное значение в исходный предел:
подлежит отдельному исследованию. Проще всего подставить данное значение в исходный предел:
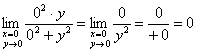
Если бы с помощью этого «полуметода» нам удалось установить несуществование предела (что бывает довольно часто), то получилось бы самое простое и короткое решение! Однако в данном случае проверка сработала «вхолостую», и на чистовике решение следует оформить «полноценным» способом:
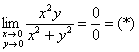
Перейдём к полярным координатам: ![]()
Если ![]() , то
, то ![]()
![]()
Полученный предел равен нулю, однако этого ещё не достаточно для существования двойного предела! И достаточный признак таков: нужно подобрать функцию ![]() – зависящую только от «эр» и стремящуюся к нулю при
– зависящую только от «эр» и стремящуюся к нулю при ![]() , такую, чтобы выполнялось неравенство:
, такую, чтобы выполнялось неравенство: ![]() хоть в какой-то окрестности (пусть очень малой) нулевого значения «эр». Тогда
хоть в какой-то окрестности (пусть очень малой) нулевого значения «эр». Тогда ![]() .
.
В нашем примере:
![]()
![]() (коль скоро «эр» и косинус квадрат неотрицательны)
(коль скоро «эр» и косинус квадрат неотрицательны)
Поскольку косинус и синус – есть функции ограниченные: ![]() то:
то:
![]() , стало быть:
, стало быть:
![]() , то есть функция
, то есть функция ![]() подобрана и двойной предел
подобрана и двойной предел
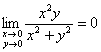 – существует.
– существует.
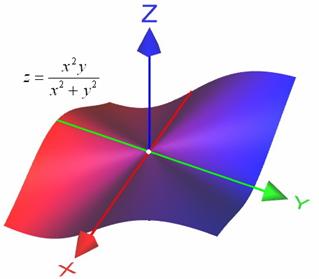
Перед вами хорошо знакомое «проколотое одеяло»:
Тройка пределов для самостоятельного решения:
Пример 3
а) 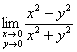
б) 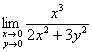
в) 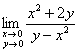
Примерный образец чистового оформления в конце урока. В пункте «б» для выяснения оценочной функции ![]() сведите знаменатель к одной тригонометрической функции, синусу либо косинусу. Это типовой приём. Ну а коварство, на которое вы наверняка попались, разберём в следующем задании:
сведите знаменатель к одной тригонометрической функции, синусу либо косинусу. Это типовой приём. Ну а коварство, на которое вы наверняка попались, разберём в следующем задании:
Пример 4
Найти предел или доказать, что его не существует
![]()
Отличительная особенность предложенной функции состоит в том, что она терпит разрыв не в единичной точке, а по кубической параболе ![]() , и поэтому в данном примере возникает одна тонкость – здесь нехорошо говорить о том, что мы «приближаемся к точке
, и поэтому в данном примере возникает одна тонкость – здесь нехорошо говорить о том, что мы «приближаемся к точке ![]() по ПРЯМЫМ
по ПРЯМЫМ ![]() ». Ведь некоторые прямые этого пучка пересекают кубическую параболу более 1-го раза и на наших путях к началу координат будут «выколотые» точки, что делает эти маршруты нелегальными.
». Ведь некоторые прямые этого пучка пересекают кубическую параболу более 1-го раза и на наших путях к началу координат будут «выколотые» точки, что делает эти маршруты нелегальными.
Тем не менее, замена ![]() всё же возможна, но подразумевать она будет лишь участки прямых (даже очень малые), по которым мы можем беспрепятственно дойти до точки
всё же возможна, но подразумевать она будет лишь участки прямых (даже очень малые), по которым мы можем беспрепятственно дойти до точки ![]()
Все эти выкладки, конечно, не нужно «вываливать на голову» рецензента – лучше использовать обтекаемую «техническую» фразу:
проведём замену ![]() :
:
![]()
Вроде бы тишь да гладь – предел не зависит от значения ![]() .
.
И если сейчас проявить небрежность, то он ответ будет неверным!
Не забываем, что у нас ещё не учтён путь по оси ![]() :
:
![]()
Вот тебе и раз! Как говорится, где тонко, там и рвётся.
Вывод: предела не существует
Интересно отметить, что метод перехода к полярным координатам (а его можно использовать) здесь очень опасен! После стандартной замены получается предел ![]() , который вовсе не равен тройке! При значениях угла
, который вовсе не равен тройке! При значениях угла ![]() (которые как раз и определяют ось ординат) в пределе получается ноль, и этот факт очень легко упустить из вида.
(которые как раз и определяют ось ординат) в пределе получается ноль, и этот факт очень легко упустить из вида.
Примечание: при подстановке этих значений «фи» в числителе получается ноль, а в знаменателе бесконечно малое значение, и при делении получается именно ноль – неопределённости ![]() тут нет !
тут нет !
Более того, даже если «эрный» предел един при любом значении «фи», то это ещё не гарантирует существования двойного предела! Нужно проверять достаточный признак либо использовать альтернативные методы обоснования, с которыми можно ознакомиться в более основательных трудах по теме. В частности (спасибо студентам МИФИ), могу порекомендовать их методичку, составитель А. Ю. Петрович, 2007 год.
И ещё пара важных абзацев, которые появились благодаря вам.
Поступил вопрос: а почему, в качестве пути приближения к предельной точке, мы безвариантно выбираем ![]() ? Потому что в большинстве примеров это просто удобно. Вообще, для доказательства несуществования общего предела достаточно найти ДВА произвольных маршрута, по которым получаются разные значения. Так, в разобранном примере можно было взять не весь пучок прямых, а лишь ось абсцисс + ось ординат. Более того, если в какой-то задаче удобнее использовать путь, например, по параболе, синусоиде и т. д., то флаг вам в руки!
? Потому что в большинстве примеров это просто удобно. Вообще, для доказательства несуществования общего предела достаточно найти ДВА произвольных маршрута, по которым получаются разные значения. Так, в разобранном примере можно было взять не весь пучок прямых, а лишь ось абсцисс + ось ординат. Более того, если в какой-то задаче удобнее использовать путь, например, по параболе, синусоиде и т. д., то флаг вам в руки!
И важнейший момент состоит в том, что пучок ![]() годится лишь для исследования начала координат! Если переменные стремятся к другой точке, то нужно взять другой пучок, прямые которого проходят именно через эту точку.
годится лишь для исследования начала координат! Если переменные стремятся к другой точке, то нужно взять другой пучок, прямые которого проходят именно через эту точку.
Спасибо и ещё раз спасибо!
Продолжаем, и в следующем примере мы как раз пронесём тот самый флаг. Эту статью я редактировал много раз, отчего Пример 5 исчез, и чтобы не сбивать нумерацию сразу::
Пример 6
Найти предел
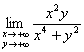
Здесь выбор пути в плоскости ![]() влияет на порядок роста числителя и знаменателя, и предел может запросто не существовать. Так, если приближаться к бесконечности по прямой
влияет на порядок роста числителя и знаменателя, и предел может запросто не существовать. Так, если приближаться к бесконечности по прямой ![]() , то:
, то:
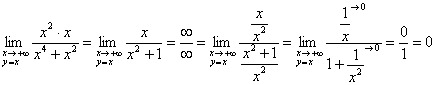 (знаменатель более высокого порядка роста, чем числитель).
(знаменатель более высокого порядка роста, чем числитель).
Но если приближаться к бесконечности по параболе ![]() , то числитель и знаменатель будут одного порядка роста, а значит, предел равен ненулевому конечному значению:
, то числитель и знаменатель будут одного порядка роста, а значит, предел равен ненулевому конечному значению:
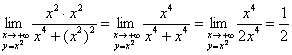
Вывод: общего предела 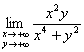 не существует.
не существует.
И в случае несущестования предела лучше использовать именно этот способ! Переход к полярным координатам крайне опасен и может привести к ошибочному выводу, за исключением пределов наподобие ![]() (Пример 1), где результат оказался зависящим только от «фи».
(Пример 1), где результат оказался зависящим только от «фи».
Помимо специфических приёмов, в ходе вычисления пределов функций двух переменных используется широкий арсенал уже известных вам методов, в частности метод замены:
Пример 7
Вычислить предел
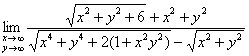
Решаем самостоятельно! Подсказывать не буду, а то получится совсем уж просто.
...Сверяемся и продолжаем:
Пример 8
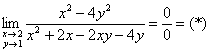
В результате прямой подстановки ![]() сталкиваемся с неопределённостью
сталкиваемся с неопределённостью ![]() , для устранения которой перспективным выглядит разложение числителя и знаменателя на множители. В числителе используем формулу разности квадратов, а в знаменателе проводим вынесение множителей за скобки (у 1-3-го и 2-4-го слагаемых):
, для устранения которой перспективным выглядит разложение числителя и знаменателя на множители. В числителе используем формулу разности квадратов, а в знаменателе проводим вынесение множителей за скобки (у 1-3-го и 2-4-го слагаемых):
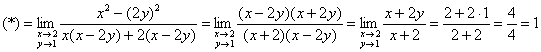
Сокращение «виновника» ![]() означает, что функция
означает, что функция ![]() терпит разрыв по типу «разрезанное одеяло» во всех точках прямой
терпит разрыв по типу «разрезанное одеяло» во всех точках прямой ![]() за исключением точки
за исключением точки ![]() . Впрочем, оставим этот материал до урока Непрерывность функции двух переменных и вернёмся к нашим баранам:
. Впрочем, оставим этот материал до урока Непрерывность функции двух переменных и вернёмся к нашим баранам:
Пример 9
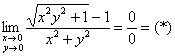
Умножим числитель и знаменатель на сопряжённое выражение:
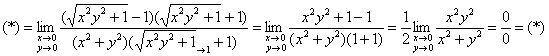
Получено нечто знакомое, перейдём к полярным координатам: ![]()
Если ![]() , то
, то ![]()
![]()
Полученный предел равен нулю, однако этого ещё не достаточно для существования двойного предела. Подбираем функцию ![]() . Ввиду ограниченности синуса и косинуса:
. Ввиду ограниченности синуса и косинуса:
![]()
Вывод: 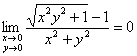
Теперь ваша парочка:
Пример 10
Найти пределы
а) 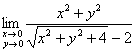
б) ![]()
Решения занимают буквально 2-3 строчки. Если возникли затруднения с пунктом «бэ», пожалуйста, посмотрите Пример 5 статьи Сложные пределы.
И, конечно же, замечательные пределы, куда без них. Рассмотрим поучительный во всех смыслах пример:
Пример 11
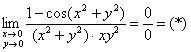
Используем до боли знакомую тригонометрическую формулу ![]() , где
, где ![]() и стандартным искусственным приёмом организуем первые замечательные пределы
и стандартным искусственным приёмом организуем первые замечательные пределы ![]() :
:
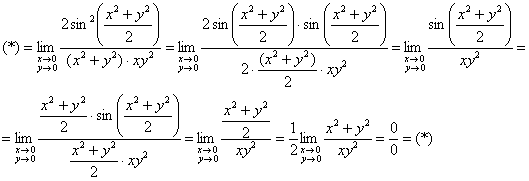
Перейдём к полярным координатам: ![]()
Если ![]() , то
, то ![]()
Казалось бы, решение идёт к закономерной развязке и ничто не предвещает неприятностей, однако в самом конце существует большой риск допустить ошибку. Сначала концовка, затем комментарий:
![]()
То есть общего предела не существует.
Почему так? Давайте посмотрим на знаменатель: так как полярный радиус неотрицателен, то он стремится к бесконечно малому положительному значению: ![]() . Кроме того,
. Кроме того, ![]() . Но есть ещё косинус, который и определяет результат:
. Но есть ещё косинус, который и определяет результат:
![]() , если полярный угол
, если полярный угол ![]() (2-я и 3-я координатные четверти:
(2-я и 3-я координатные четверти: ![]() );
);
![]() , если полярный угол
, если полярный угол ![]() (1-я и 4-я координатные четверти:
(1-я и 4-я координатные четверти: ![]() ).
).
Геометрически это означает, что если приближаться к началу координат слева, то поверхность, заданная функцией ![]() , простирается до бесконечности вниз:
, простирается до бесконечности вниз:
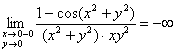
и если справа – то вверх:
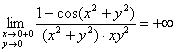
А между погружением на дно океана и полётом за облака, мягко говоря, есть разница.
Задание для самостоятельного решения:
Пример 12
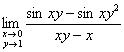
Краткое решение и ответ в концу урока. Как видите, с технической точки зрения ничего особенно нового-то, и нет.
Вместо замечательных пределов можно использовать и замечательные эквивалентности:
Пример 13
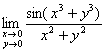
Вспоминаем мотив: при ![]() справедлива эквивалентность
справедлива эквивалентность ![]() . В данном случае
. В данном случае ![]() и после эквивалентной замены получаем предел
и после эквивалентной замены получаем предел 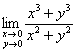 . Почему это корректно? В достаточно малой окрестности точки
. Почему это корректно? В достаточно малой окрестности точки ![]() поверхность,
поверхность, ![]() практически совпадает с поверхностью
практически совпадает с поверхностью ![]() , и поэтому одну функцию можно безболезненно заменить другой.
, и поэтому одну функцию можно безболезненно заменить другой.
На втором шаге переходим к полярным координатам, после чего ![]() превращается в
превращается в ![]() , а примелькавшаяся сумма
, а примелькавшаяся сумма ![]() – в
– в ![]() . По итогу:
. По итогу:
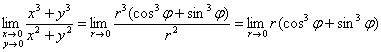
и коль скоро ![]() ,
,
то 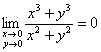 , а значит, в силу эквивалентности, нулю равен и исходный предел:
, а значит, в силу эквивалентности, нулю равен и исходный предел:
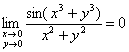 .
.
Желающие могут прорешать Примеры 11, 12 вторым способом, что, кстати, проще
Проверьте, насколько хорошо вы усвоили урок о бесконечно малых функциях:
Пример 14
Найти предел функции двух переменных
![]()
Решение совсем близко.
И заключительные примеры статьи посвящены второму замечательному пределу:
Пример 15
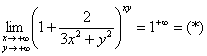
Приём решения такой же: делаем дробь трёхэтажной и искусственным возведением в степень организуем второй замечательный предел ![]() :
:

В силу непрерывности экспоненциальной функции, значок предела можно перенести в показатель: 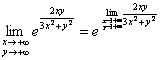
Чтобы не возиться с мелкими символами, предел показателя удобно найти отдельно:
![]()
И тут лучше использовать метод «опровержения», рассмотрев 2 пути – по прямой и параболе, поскольку они меняют порядок роста числителя и знаменателя, что нетрудно углядеть; всегда проверяйте этот перспективный вариант. Идём к бесконечности по прямой ![]() :
:
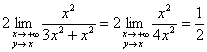
Теперь по параболе ![]() :
:
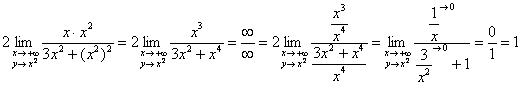
Предел зависит от пути, поэтому предела ![]() , а значит, и предела
, а значит, и предела ![]() не существует.
не существует.
Готово!
И, как я уже отмечал в самом начале, на практике вам вполне могут предложить вычислить не общий предел, а предел по какому-либо частному пути, да тот же самый: «вычислить предел 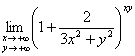 по направлению прямой
по направлению прямой ![]() ». Проблем вообще никаких:
». Проблем вообще никаких:

Существует и частный предел по «школьной» параболе, который, очевидно, равен ![]() .
.
На посошок:
Пример 16
Вычислить предел функции двух переменных или доказать, что его не существует:
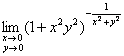
Всё очень просто!
Материалов данного урока должно хватить для решения большинства практических примеров по теме, но, тем не менее, на следующих занятиях (Повторные пределы и Непрерывность функции двух переменных), мы продолжим работать с пределами функций двух переменных, и, более того, я расскажу вам ещё об одном эффективном методе их решения.
Спасибо за активное участие и до скорых встреч!
Решения и ответы:
Пример 3. Решение:
а) 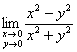
Проведём замену ![]()
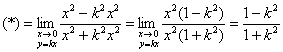
Результат зависит от коэффициента ![]() , значит, данного предела не существует
, значит, данного предела не существует
б) 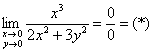
Функция терпит разрыв в начале координат.
Перейдём к полярным координатам: ![]()
Если ![]() , то
, то ![]()
![]()
Функция ![]() при
при ![]() , но этого ещё не достаточно для существования двойного предела. Подберём функцию
, но этого ещё не достаточно для существования двойного предела. Подберём функцию ![]() , такую, что:
, такую, что:
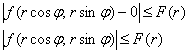
Поскольку косинус ограничен, то ![]() , и:
, и:
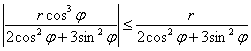 (знаменатель положителен), и для дальнейшей оценки преобразуем нижний этаж, используем основное тригонометрическое тождество:
(знаменатель положителен), и для дальнейшей оценки преобразуем нижний этаж, используем основное тригонометрическое тождество:
![]()
Таким образом: ![]()
Так как ![]() , то
, то ![]() , то есть в зависимости от угла «фи» получаем пучок линейных функций от
, то есть в зависимости от угла «фи» получаем пучок линейных функций от ![]() до
до ![]() . В качестве оценочной функции можно выбрать последнюю
. В качестве оценочной функции можно выбрать последнюю ![]() либо другую линейную функцию с бОльшим угловым коэффициентом.
либо другую линейную функцию с бОльшим угловым коэффициентом.
Кратко рассуждения можно записать так:
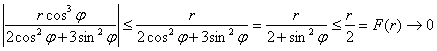
Вывод: 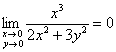
в) Вычислим предел по оси абсцисс:
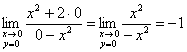
Вычислим предел по оси ординат:
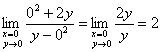
Вывод: общего предела не существует
Пример 7. Решение:
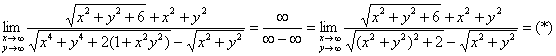
Проведём замену переменной: ![]()
Если ![]() , то
, то ![]()
![]()
Разделим числитель и знаменатель на ![]()
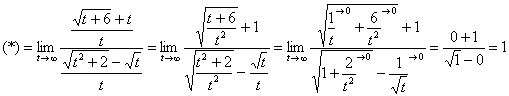
Пример 10. Решение:
а) 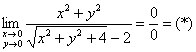
Умножим числитель и знаменатель на сопряжённое выражение
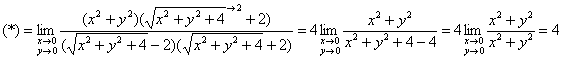
б) ![]()
Умножим числитель и знаменатель на сопряжённое выражение
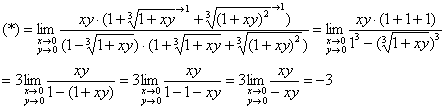
Пример 12. Решение:
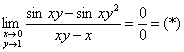
Используем формулу ![]() и первый замечательный предел.
и первый замечательный предел.
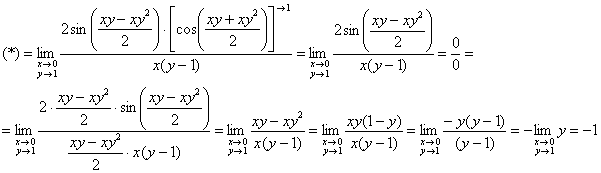
Пример 14. Решение:
![]()
Поскольку ![]() и
и ![]() , то
, то ![]() ;
;
поскольку ![]() , то
, то ![]()
![]()
Проведём замену: ![]()
![]()
Результат зависит от ![]() , поэтому предела не существует.
, поэтому предела не существует.
Пример 16. Решение:
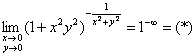
Используем 2-й замечательный предел в виде ![]()
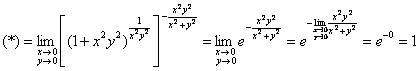
Примечание: предел 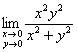 найден в Примере 9
найден в Примере 9
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright