


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Конформное отображение.
Растяжение и угол поворота. Длина и площадь образа
Спокойствие, только спокойствие (с)
И вновь эта волшебная цитата помогает нам обрести самообладание! Скоро мы разберёмся во всех словах заголовка, с толком, расстановкой, не спеша – одно за другим. Само собой, будут и практические примеры, с банкой варенья и плюшками решениями и подробными объяснениями. Начинаем, или как сейчас модно говорить, поехали (с)
На первом занятии по комплексному анализу мы познакомились с понятием функции комплексной переменной ![]() . Это и есть отображение. В общем случае оно отображает разные линии плоскости
. Это и есть отображение. В общем случае оно отображает разные линии плоскости ![]() в разные линии плоскости
в разные линии плоскости ![]() , чему мы воочию убедились на уроке Как отобразить линию и область с помощью комплексной функции? При этом прямая может запросто превратиться в кривую или наоборот, а уж кривая в иную кривую – подавно.
, чему мы воочию убедились на уроке Как отобразить линию и область с помощью комплексной функции? При этом прямая может запросто превратиться в кривую или наоборот, а уж кривая в иную кривую – подавно.
И для пущей наглядности отобразим прямоугольную «сетку» плоскости ![]() (см. чертёж ниже). Что мы видим по итогу на плоскости
(см. чертёж ниже). Что мы видим по итогу на плоскости ![]() ? …Смещение точек. …Поворот «сетки», причём в разных местах – на разные углы. Её искажение, тоже неравномерное: в районе точки
? …Смещение точек. …Поворот «сетки», причём в разных местах – на разные углы. Её искажение, тоже неравномерное: в районе точки ![]() наблюдается растяжение, а в районе
наблюдается растяжение, а в районе ![]() – сжатие. Вспоминая алгебру, то, что изображено слева, называют прообразом отображения, а результат справа – образом отображения.
– сжатие. Вспоминая алгебру, то, что изображено слева, называют прообразом отображения, а результат справа – образом отображения.
Но это всё общие признаки, характерные для многих функций. Однако среди них есть особый класс – конформные отображения, которые сохраняют углы между линиями. И такой пример приведён на иллюстрации. Рассмотрим точку ![]() , которую функция
, которую функция ![]() перевела в точку
перевела в точку ![]() . При этом прямая
. При этом прямая ![]() отобразилась в верхнюю кривую, проведём касательную
отобразилась в верхнюю кривую, проведём касательную ![]() к этой кривой в точке
к этой кривой в точке ![]() . Аналогично, прямая
. Аналогично, прямая ![]() отобразилась в левую кривую с касательной
отобразилась в левую кривую с касательной ![]() . Угол
. Угол ![]() – есть угол между кривыми-образами. …Разобрались?
– есть угол между кривыми-образами. …Разобрались?
Конформное отображение сохранило угол (в данном случае прямой) между прообразами и образами: ![]() . При этом в точке
. При этом в точке ![]() был осуществлён поворот «картинки» на угол
был осуществлён поворот «картинки» на угол ![]() , назовём его углом поворота. В данном случае это поворот против часовой стрелки, «на глазок» градусов на 30:
, назовём его углом поворота. В данном случае это поворот против часовой стрелки, «на глазок» градусов на 30:
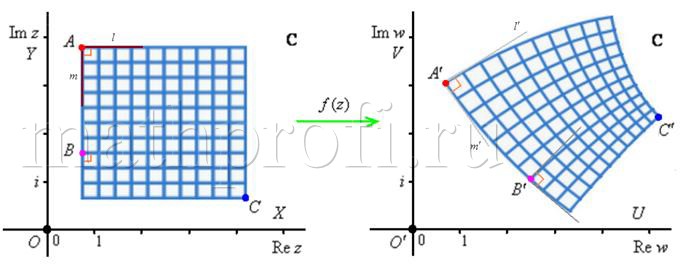
Очевидно, в разных точках углы поворота будут разными (в общем случае), так при отображении точки ![]() он составляет где-то около 45 градусов, и коль скоро оно конформное, то, естественно, сохранён прямой угол.
он составляет где-то около 45 градусов, и коль скоро оно конформное, то, естественно, сохранён прямой угол.
Более того, конформное отображение сохраняет вообще все углы (не только прямые) между произвольными линиями, проведёнными через точку. Возьмите в руки карандаш (да-да, реально возьмите), нарисуйте систему ![]() и поставьте точку
и поставьте точку ![]() в том же месте. Проведите через неё две гладкие кривые (любые) и касательные
в том же месте. Проведите через неё две гладкие кривые (любые) и касательные ![]() к ним. Угол между касательными
к ним. Угол между касательными ![]() – есть угол
– есть угол ![]() между кривыми. Так вот, конформное отображение
между кривыми. Так вот, конформное отображение ![]() : 1) сохранит угол
: 1) сохранит угол ![]() в точке
в точке ![]() между линиями-образами (касательными
между линиями-образами (касательными ![]() к ним):
к ним): ![]() и 2) осуществит поворот «картинки» на тот же самый угол поворота
и 2) осуществит поворот «картинки» на тот же самый угол поворота ![]() .
.
…Если не осилили, вдумчиво перечитайте материал ещё раз. Главное тут не запутаться в углах: угол поворота постоянен (в той или иной точке), а вот углы между произвольными линиями могут быть любыми – и их конформное отображение сохраняет. Можно ещё сказать так: бесконечно малый треугольник с вершиной в точке ![]() отображается в подобный ему (с теми же углами) бесконечно малый криволинейный (в общем случае) треугольник с вершиной в точке
отображается в подобный ему (с теми же углами) бесконечно малый криволинейный (в общем случае) треугольник с вершиной в точке ![]() , повёрнутый на угол
, повёрнутый на угол ![]() . Вместо треугольника, разумеется, можно рассмотреть другую геометрическую фигуру. Такой вот математический калейдоскоп.
. Вместо треугольника, разумеется, можно рассмотреть другую геометрическую фигуру. Такой вот математический калейдоскоп.
А вот примеры неконформного отображения прямоугольной «сетки», выражаю благодарность вольному художнику Википедии, откуда я позаимствовал этот и часть предыдущего чертежа:
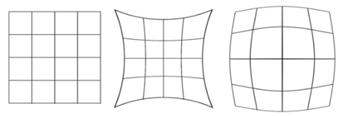
Здесь углы между линиями не сохраняются. …Долго не смотрИте, не комфортно.
Хотел всё объяснить покороче, но покороче не получилось :) Теперь ближе к практике.
Функция ![]() , регулярная (аналитичная) в области, осуществляет конформное отображение этой области – в тех точках, где её производная отлична от нуля:
, регулярная (аналитичная) в области, осуществляет конформное отображение этой области – в тех точках, где её производная отлична от нуля: ![]() . Причём, модуль производной
. Причём, модуль производной ![]() в точке
в точке ![]() равен коэффициенту изменения масштаба при отображении точки
равен коэффициенту изменения масштаба при отображении точки ![]() (её достаточно малой окрестности), а аргумент
(её достаточно малой окрестности), а аргумент ![]() – есть в точности угол поворота.
– есть в точности угол поворота.
Если ![]() , то в достаточно малой окрестности точки
, то в достаточно малой окрестности точки ![]() расстояния между точками при отображении увеличиваются в
расстояния между точками при отображении увеличиваются в ![]() раз, то есть происходит растяжение. Если же
раз, то есть происходит растяжение. Если же ![]() то имеет место сжатие в
то имеет место сжатие в ![]() раз. И совершенно понятна ситуация с аргументом: при
раз. И совершенно понятна ситуация с аргументом: при ![]() угол поворота осуществляется против часовой стрелки, а при
угол поворота осуществляется против часовой стрелки, а при ![]() – по часовой.
– по часовой.
Следует добавить, что регулярность функции является достаточным, но не необходимым условием конформности, то есть существуют неаналитические функции, которые, тем не менее, осуществляют конформное отображение.
Рассмотрим два «классических» примера, один из которых был в самом начале курса:
![]() – эта функция, очевидно, «вытягивает» все точки плоскости
– эта функция, очевидно, «вытягивает» все точки плоскости ![]() в два раза (за исключением начала координат), отображая их на плоскость
в два раза (за исключением начала координат), отображая их на плоскость ![]() – мысленно подставьте любое ненулевое
– мысленно подставьте любое ненулевое ![]() . Таким образом, ситуация понятна и без производной, однако проведём исследование формально.
. Таким образом, ситуация понятна и без производной, однако проведём исследование формально.
Как легко выяснить, эта функция дифференцируема на всей комплексной плоскости: ![]() , а значит, регулярна в ней и осуществляют конформное отображение всюду, коль скоро производная ненулевая константа. Так как
, а значит, регулярна в ней и осуществляют конформное отображение всюду, коль скоро производная ненулевая константа. Так как ![]() для любого «зет», то происходит растяжение плоскости
для любого «зет», то происходит растяжение плоскости ![]() в два раза при отображении её на
в два раза при отображении её на ![]() , при этом поворот везде нулевой – по той причине, что аргумент
, при этом поворот везде нулевой – по той причине, что аргумент ![]() .
.
Нетрудно понять, что функция ![]() выполняет хорошо знакомое нам преобразование подобия (гомотетию) с масштабирующим коэффициентом «ка».
выполняет хорошо знакомое нам преобразование подобия (гомотетию) с масштабирующим коэффициентом «ка».
Теперь второй пример, ![]() . Эта функция тоже аналитична на всей комплексной плоскости:
. Эта функция тоже аналитична на всей комплексной плоскости: ![]() , но отображение конформно уже не везде. А именно, неконформно оно в начале координат, где производная обращается в ноль
, но отображение конформно уже не везде. А именно, неконформно оно в начале координат, где производная обращается в ноль ![]() . Углы между линиями, проходящими через точку
. Углы между линиями, проходящими через точку ![]() , не сохраняются, а увеличиваются в два раза (обоснование этого факта можно найти в учебной литературе).
, не сохраняются, а увеличиваются в два раза (обоснование этого факта можно найти в учебной литературе).
И для окончательного понимания рассмотрим какую-нибудь «хорошую» точку, возьмём ![]() , и вычислим производную в ней:
, и вычислим производную в ней: ![]() . Определим модуль и аргумент полученного значения:
. Определим модуль и аргумент полученного значения:
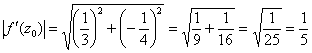
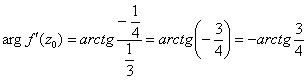
Итак, представьте две произвольные линии, проходящие через точку ![]() и угол между ними (угол между соответствующими касательными). Что делает конформное отображение
и угол между ними (угол между соответствующими касательными). Что делает конформное отображение ![]() в бесконечно малой окрестности точки
в бесконечно малой окрестности точки ![]() ?
?
1) Переводит эти линии в другие линии (общий случай) на плоскости ![]() и сохраняет углы между ними.
и сохраняет углы между ними.
2) Уменьшает масштаб в 5 раз, ибо ![]() , то есть образы (полученные линии) оказываются в 5 раз меньше прообразов.
, то есть образы (полученные линии) оказываются в 5 раз меньше прообразов.
3) Осуществляет поворот на ![]() (по часовой стрелке), то есть образы оказываются повёрнуты на этот угол по отношению к прообразам.
(по часовой стрелке), то есть образы оказываются повёрнуты на этот угол по отношению к прообразам.
И мы переходим к реальным задачам, формулировка которых малопонятна для неискушенного читателя, впрочем, их можно решить и чисто формально – безо всякого понимания:
Пример 1
Найти коэффициенты изменения масштаба и углы поворота при отображении ![]() в точках
в точках ![]() ,
, ![]()
Решение: как мы выяснили на практикуме по производным, элементарные функции комплексной переменной регулярны в своих областях определения, следовательно, осуществляют конформное отображение… в тех, точках, где производная отлична от нуля – не забываем об этом условии!
Берём производную-мечту: ![]() , и для удобства сразу представим её в алгебраической форме. Так как
, и для удобства сразу представим её в алгебраической форме. Так как ![]() , то по свойству степеней и формуле Эйлера:
, то по свойству степеней и формуле Эйлера:
![]()
1) Определим коэффициент изменения масштаба и угол поворота в точке ![]() . Для неё
. Для неё ![]() и по только полученной формуле:
и по только полученной формуле:
![]()
Вычислим модуль полученного значения, то есть коэффициент масштабирования:
![]() – вот оно как! Таким образом, в бесконечно малой окрестности точки
– вот оно как! Таким образом, в бесконечно малой окрестности точки ![]() функция
функция ![]() не меняет масштаб образов (по отношению к прообразами).
не меняет масштаб образов (по отношению к прообразами).
Определим аргумент, то есть угол поворота:
![]() – таким образом, в бесконечно малой окрестности точки
– таким образом, в бесконечно малой окрестности точки ![]() функция
функция ![]() осуществляет поворот отображаемых точек на один радиан против часовой стрелки.
осуществляет поворот отображаемых точек на один радиан против часовой стрелки.
И самое главное, конформное отображение ![]() сохранило углы между линиями, проходящими через точку
сохранило углы между линиями, проходящими через точку ![]() (в её бесконечно малой окрестности). Более того, углы сохраняются в любой точке комплексной плоскости, ибо экспонента регулярна всюду и её производная нигде не обращается в ноль
(в её бесконечно малой окрестности). Более того, углы сохраняются в любой точке комплексной плоскости, ибо экспонента регулярна всюду и её производная нигде не обращается в ноль ![]() .
.
2) На очереди точка ![]() . Для неё
. Для неё ![]() и по той же формуле
и по той же формуле ![]() получаем:
получаем:
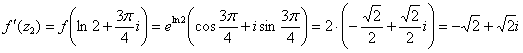
Вычислим коэффициент масштабирования:
![]() – таким образом, в бесконечно малой окрестности точки
– таким образом, в бесконечно малой окрестности точки ![]() образы оказываются в два раза больше прообразов, то есть функция
образы оказываются в два раза больше прообразов, то есть функция ![]() выполнила двукратное растяжение.
выполнила двукратное растяжение.
Найдём угол поворота. Поскольку значение производной лежит во 2-й координатной четверти, то аргумент рассчитывается по несколько другой формуле:
![]() – таким образом, итоговая «картинка» повёрнута на 135 градусов против часовой стрелки (относительно прообраза)
– таким образом, итоговая «картинка» повёрнута на 135 градусов против часовой стрелки (относительно прообраза)
Готово.
На практике коэффициент масштабирования также называют коэффициентом искажения масштаба, а чаще коэффициентом растяжения, подразумевая, что это частности может оказаться и сжатием. Вот типовая формулировка и задание для самостоятельного решения:
Пример 2
Найти коэффициент растяжения ![]() и угол поворота
и угол поворота ![]() при заданных отображениях
при заданных отображениях ![]() в данных точках:
в данных точках:
1) ![]() в точке
в точке ![]() , вновь справочно приведу формулы:
, вновь справочно приведу формулы:
![]()
2) ![]() в точке
в точке ![]() .
.
Сделать выводы.
Решаем, сверяемся (внизу страницы) и продолжаем. Те же задачи, в более затейливой вариации:
Пример 3
Дано отображение ![]()
а) Найти множество точек, в которых коэффициент растяжения равен единице.
б) Выяснить, в каких точках комплексной плоскости угол поворота равен нулю.
Решение: элементарная функция ![]() регулярна на всей комплексной плоскости, найдём её производную:
регулярна на всей комплексной плоскости, найдём её производную: ![]() . Очевидно, отображение конформно всюду, кроме начала координат, где производная обращается в ноль. Обращаю внимание, что точка
. Очевидно, отображение конформно всюду, кроме начала координат, где производная обращается в ноль. Обращаю внимание, что точка ![]() сразу исключается из рассмотрения, так как в ней не идёт речи о коэффициенте растяжения и угле поворота (о постоянстве этих величин).
сразу исключается из рассмотрения, так как в ней не идёт речи о коэффициенте растяжения и угле поворота (о постоянстве этих величин).
а) Выделим действительную и мнимую часть производной. Так как ![]() , то:
, то:
![]()
Составим функцию модуля производной:
![]() – в результате получена функция двух действительных переменных, которая каждому комплексному «зет» ставит в соответствие модуль производной в этой точке. Обозначим её буквой
– в результате получена функция двух действительных переменных, которая каждому комплексному «зет» ставит в соответствие модуль производной в этой точке. Обозначим её буквой ![]() , ибо она возвращает нам коэффициент растяжения.
, ибо она возвращает нам коэффициент растяжения.
По условию, нужно найти множество точек, в которых коэффициент растяжения равен единице:
![]()
и после простецких манипуляций выясняем, что это:
![]()
![]() – окружность с центром в начале координат радиуса
– окружность с центром в начале координат радиуса ![]()
Во всех точках этой окружности (их бесконечно малых окрестностях) конформное отображение ![]() сохраняет масштаб неизменным (не сжимает и не растягивает расстояния между отображаемыми точками).
сохраняет масштаб неизменным (не сжимает и не растягивает расстояния между отображаемыми точками).
б) Выясним, в каких точках комплексной плоскости угол поворота равен нулю, а именно, это те точки ![]() , в которых
, в которых ![]() . Вытащим на свет громоздкую формулу аргумента:
. Вытащим на свет громоздкую формулу аргумента:
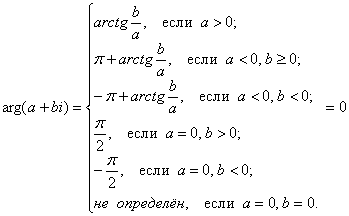
Теперь нужно выбрать нужную «ветку». Значению ![]() (нулевому углу) соответствуют числа, лежащие на действительной положительной полуоси, а они удовлетворяют условию
(нулевому углу) соответствуют числа, лежащие на действительной положительной полуоси, а они удовлетворяют условию ![]() . Что соответствует первой строчке формулы:
. Что соответствует первой строчке формулы:
![]()
Как мы выясняли в предыдущем пункте, ![]() , таким образом,
, таким образом, ![]() и уравнение
и уравнение ![]() принимает вид:
принимает вид:
![]() , и здесь очень важно не потерять условие
, и здесь очень важно не потерять условие ![]() , из которого сразу следует, что
, из которого сразу следует, что ![]() (вспоминаем элементарные неравенства).
(вспоминаем элементарные неравенства).
Теперь разруливаем уравнение: сокращаем на двойку, выносим из-под арктангенса «минус» (нечётность) и избавляемся от «минуса»:
![]()
Таким образом:
![]() , откуда следует, что
, откуда следует, что ![]()
В результате получаем множество чисел ![]() с нулевой действительной частью, то бишь это точки
с нулевой действительной частью, то бишь это точки ![]() мнимой оси, причём только её нижней части – ввиду условия
мнимой оси, причём только её нижней части – ввиду условия ![]() .
.
Вывод: конформное отображение ![]() не поворачивает отображаемые объекты в точках
не поворачивает отображаемые объекты в точках ![]() (их бесконечно малых окрестностях).
(их бесконечно малых окрестностях).
Ответ: а) ![]() , б)
, б) ![]() .
.
Эпичная функция, и задания пусть будут позанятнее:
Пример 4
Выяснить, какая часть комплексной плоскости растягивается / сжимается / остаётся неизменной при отображении ![]() . Определить множество точек, где оно осуществляет поворот на 90 градусов, на 135 градусов.
. Определить множество точек, где оно осуществляет поворот на 90 градусов, на 135 градусов.
Решаем самостоятельно, формула Эйлера в помощь, а также памятка по простейшим тригонометрическим уравнениям и неравенствам, а то с углами переборщил я малость :) Хотя, в сборниках есть и технически более сложные примеры. Сверяемся с образцом внизу страницы и переходим к следующей теме.
Длина и площадь образа отображения
Здесь проще разобраться на конкретном примере, скопирую картинку из Примера 4 урока Как отобразить линию и область с помощью комплексной функции. В той задаче мы отобразили область ![]() (прообраз) в область
(прообраз) в область ![]() (образ) с помощью функции
(образ) с помощью функции ![]() :
:
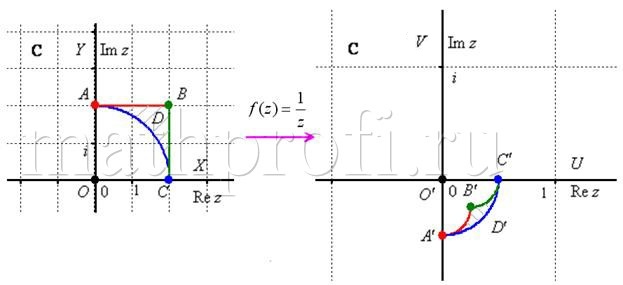
И сейчас мы хотим найти площадь области ![]() (образа отображения). Она рассчитывается по формуле
(образа отображения). Она рассчитывается по формуле ![]() – то есть как двойной интеграл по прообразу (области
– то есть как двойной интеграл по прообразу (области ![]() ) от функции
) от функции ![]() , которая характеризует коэффициент искажения площади при отображении
, которая характеризует коэффициент искажения площади при отображении ![]() .
.
И, кроме того, нас будут интересовать длины. Так, линия ![]() (прообраз) отобразилась в
(прообраз) отобразилась в ![]() (образ), и мы хотим вычислить длину образа. Она рассчитывается по формуле
(образ), и мы хотим вычислить длину образа. Она рассчитывается по формуле ![]() , где
, где ![]() – как криволинейный интеграл по прообразу
– как криволинейный интеграл по прообразу ![]() , в данном примере – по отрезку
, в данном примере – по отрезку ![]() .
.
Эти формулы работают, если отображение ![]() регулярно в рассматриваемой области, а функция
регулярно в рассматриваемой области, а функция ![]() регулярна всюду, кроме нуля, и мы продолжим её пилить:
регулярна всюду, кроме нуля, и мы продолжим её пилить:
Пример 5
Найти длины линий ![]() в примере выше и площадь области
в примере выше и площадь области ![]() .
.
Решение начнём с длин:
1) Найдём длину линии ![]() . И тут на самом деле есть варианты. В Примере 4 мы нашли уравнение этой дуги
. И тут на самом деле есть варианты. В Примере 4 мы нашли уравнение этой дуги ![]() в системе
в системе ![]() и можно преспокойно использовать стандартную формулу длины дуги кривой. Но сейчас перед нами открылась другая возможность и спокойствие только снится:)
и можно преспокойно использовать стандартную формулу длины дуги кривой. Но сейчас перед нами открылась другая возможность и спокойствие только снится:)
![]()
Найдём производную: 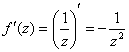 и определим её действительную и мнимую часть. Так как
и определим её действительную и мнимую часть. Так как ![]() , то:
, то:
![]()
Умножим числитель и знаменатель на сопряжённое выражение, чтобы воспользоваться формулой ![]() :
:
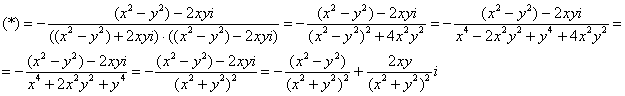
Составим функцию модуля производной:
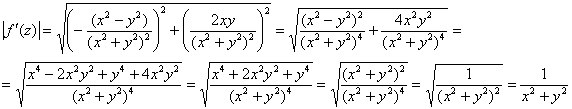
И заряжаем криволинейный интеграл 2-го рода:
![]()
Линия ![]() представляет собой отрезок прямой
представляет собой отрезок прямой ![]() , дифференциал
, дифференциал ![]() , таким образом
, таким образом ![]() . Как раскрывать модуль? Поскольку мы собрались интегрировать в «обычном» направлении
. Как раскрывать модуль? Поскольку мы собрались интегрировать в «обычном» направлении ![]() , то бесконечно малое приращение
, то бесконечно малое приращение ![]() будет положительным, поэтому модуль следует раскрыть со знаком «плюс»:
будет положительным, поэтому модуль следует раскрыть со знаком «плюс»: ![]() . Следует заметить, что интегрировать можно и от 2 до 0 (от точки
. Следует заметить, что интегрировать можно и от 2 до 0 (от точки ![]() до точки
до точки ![]() ) и тогда модуль раскрывается со знаком «минус».
) и тогда модуль раскрывается со знаком «минус».
Продолжаем:
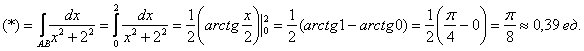 – длина образа (дуги
– длина образа (дуги ![]() ).
).
И проверка здесь простА, в Примере 4 мы получили уравнение, на которой лежит эта дуга: ![]() – уравнение окружности радиуса
– уравнение окружности радиуса ![]() . По элементарной формуле, её длина составляет
. По элементарной формуле, её длина составляет ![]() , а дуга
, а дуга ![]() , как хорошо видно по чертежу – четвертинка этой длины:
, как хорошо видно по чертежу – четвертинка этой длины: ![]() . Возможно, вам показалось это проще, но тут ещё нужно отыскать уравнение, и не факт, что получится что-то «хорошее».
. Возможно, вам показалось это проще, но тут ещё нужно отыскать уравнение, и не факт, что получится что-то «хорошее».
2) Длина линии ![]() рассчитывается «зеркально». Отрезок
рассчитывается «зеркально». Отрезок ![]() лежит на прямой
лежит на прямой ![]() , таким образом:
, таким образом: ![]() – со знаком «минус» – для разнообразия проинтегрируем по убыванию переменной (и, собственно, от точки
– со знаком «минус» – для разнообразия проинтегрируем по убыванию переменной (и, собственно, от точки ![]() до
до ![]() ), «игрек» изменяется от 2 до 0:
), «игрек» изменяется от 2 до 0:
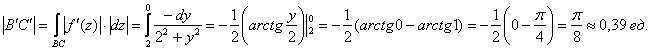
3) И, наконец, длина линии ![]() :
:
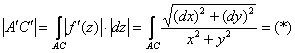
И решить этот интеграл можно не единственным способом. Сначала разберём интегрирование по «икс» либо «игрек», выберем «традиционный» вариант. Из уравнения окружности ![]() выразим функцию верхней полуокружности
выразим функцию верхней полуокружности ![]() , на которой лежит дуга
, на которой лежит дуга ![]() , и найдём её дифференциал:
, и найдём её дифференциал:
![]()
Теперь упростим верхний этаж, полагая, что интегрировать будем в «традиционном» направлении:
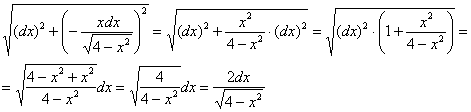
Интегрируем по «икс», при этом ![]() , интеграл опять табличный:
, интеграл опять табличный:

Дуга ![]() лежит на окружности
лежит на окружности ![]() и проверка опять же элементарна: длина окружности
и проверка опять же элементарна: длина окружности ![]() , а дуга (см. чертёж) – её четверть:
, а дуга (см. чертёж) – её четверть: ![]() .
.
Альтернативный и более простой способ расчёта интеграла состоит в использовании параметра:
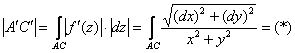
Запишем параметрические уравнения окружности ![]() , на которой лежит дуга
, на которой лежит дуга ![]() :
: ![]() , и знаменатель сразу приятно упрощается:
, и знаменатель сразу приятно упрощается:
![]()
Найдём ![]() и составим общий дифференциал:
и составим общий дифференциал:
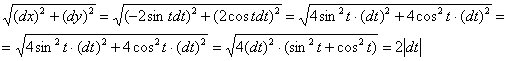
Чтобы раскрыть модуль выясним пределы и направление изменения параметра. Точке ![]() соответствует значение
соответствует значение ![]() , точке
, точке ![]() :
: ![]() . Таким образом, при интегрировании в этом направлении значение параметра будет убывать, стало быть, его бесконечно малое приращение «дэ тэ» отрицательно:
. Таким образом, при интегрировании в этом направлении значение параметра будет убывать, стало быть, его бесконечно малое приращение «дэ тэ» отрицательно: ![]()
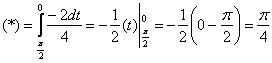
4) Вычислим площадь образа (области «дэ штрих») с помощью двойного интеграла, по формуле:
![]()
И здесь лучше перейти к полярным координатам. Область «дэ» придётся разделить на две части, но из соображений симметрии я прорешаю только один кусок. Сначала запишем уравнение прямой ![]() в полярных координатах, и тут неожиданно подоспел новенький материал :) На первом курсе я вроде досконально разобрал прямую на плоскости, но кое-что потребовалось только сейчас. Если прямая задана общим уравнением
в полярных координатах, и тут неожиданно подоспел новенький материал :) На первом курсе я вроде досконально разобрал прямую на плоскости, но кое-что потребовалось только сейчас. Если прямая задана общим уравнением ![]() , то её полярное уравнение имеет вид
, то её полярное уравнение имеет вид ![]() .
.
Для прямой ![]() .
.
Перейдём к полярной системе координат: ![]() , чтобы чудесным образом упростить знаменатель:
, чтобы чудесным образом упростить знаменатель:
![]()
Область ![]() разделим на две части по лучу
разделим на две части по лучу ![]() (на чертеже не изображён), при этом порядок обхода нижней части таков:
(на чертеже не изображён), при этом порядок обхода нижней части таков:
![]() (от окружности
(от окружности ![]() до прямой
до прямой ![]() );
);
![]()
да, и не забываем удвоить площадь, ибо картинка симметричная; желающие могут провести вычисления для второго куска, где ![]() .
.
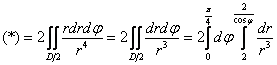
Возьмём внутренний интеграл:
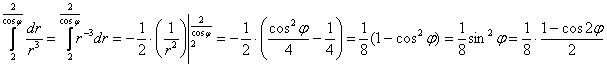 – подставим во внешний интеграл, не забывая, что там ещё есть множитель-«двойка»:
– подставим во внешний интеграл, не забывая, что там ещё есть множитель-«двойка»:
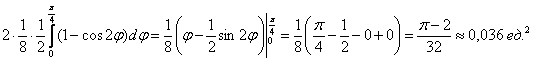 – площадь образа (области «дэ штрих»).
– площадь образа (области «дэ штрих»).
На «глазок» результат кажется слишком маленьким, но это иллюзия – ведь я существенно увеличил чертёж и область ![]() весьма малА.
весьма малА.
В лучших традициях выложим в ряд головы дракона,
ответ: ![]() ,
, ![]() ,
, ![]()
И тот самый «Пакмэн» для самостоятельного решения:
Пример 6
Дано отображение:
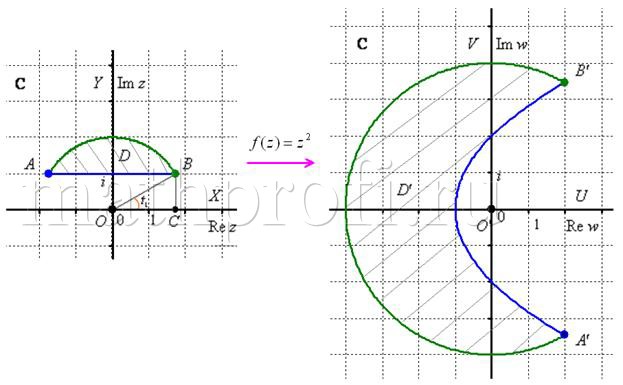
Требуется:
0) Найти угол поворота и коэффициент искажения в точке ![]() – это так, шутя, и вычислить:
– это так, шутя, и вычислить:
1) длину образа отрезка ![]() ;
;
2) длину образа дуги ![]() ;
;
3) площадь ![]() .
.
Для пункта 3 угол уже найден (Пример 5), он хороший ![]() – смело переходИте к полярным координатам, получившийся интеграл сведите к котангенсу и его производной (см. Примеры 15-16 урока Сложные интегралы, там же, к слову, есть интеграл пункта 1).
– смело переходИте к полярным координатам, получившийся интеграл сведите к котангенсу и его производной (см. Примеры 15-16 урока Сложные интегралы, там же, к слову, есть интеграл пункта 1).
…Душевное у нас получилось занятие, немногие дожили до концовки :) Но оно стоило того – многое, что было изучено ранее – развернулось во всей красе.
Курс на интегралы! (ожидаются)
Решения и ответы:
Пример 2. Решение:
1) Функция ![]() дифференцируема на всей комплексной плоскости:
дифференцируема на всей комплексной плоскости:
![]() – но, обратите внимание, что косинус обращается в ноль в точках
– но, обратите внимание, что косинус обращается в ноль в точках ![]() , поэтому в них отображение
, поэтому в них отображение ![]() неконформно. Однако точка
неконформно. Однако точка ![]() не принадлежит этому множеству.
не принадлежит этому множеству.
Так как ![]() , то по соответствующей формуле:
, то по соответствующей формуле:
![]()
Вычислим значение производной в точке ![]() :
:
![]()
=![]() (использовали нечётность гиперболического синуса).
(использовали нечётность гиперболического синуса).
Вычислим коэффициент растяжения:
![]() – таким образом, в бесконечно малой окрестности точки
– таким образом, в бесконечно малой окрестности точки ![]() отображение
отображение ![]() увеличивает масштаб примерно в 1,175 раза.
увеличивает масштаб примерно в 1,175 раза.
Число ![]() лежит на мнимой оси и, очевидно, что:
лежит на мнимой оси и, очевидно, что:
![]() – таким образом, отображаемые объекты поворачиваются на 90 градусов по часовой стрелке.
– таким образом, отображаемые объекты поворачиваются на 90 градусов по часовой стрелке.
2) Функция ![]() дифференцируема на всей комплексной плоскости:
дифференцируема на всей комплексной плоскости:
![]() и осуществляет конформное отображение во всех точках, за исключением нуля (где производная равна нулю). Кстати, «на провокацию» значение
и осуществляет конформное отображение во всех точках, за исключением нуля (где производная равна нулю). Кстати, «на провокацию» значение ![]() может быть предложено для решения.
может быть предложено для решения.
Вычислим значение производной в точке ![]() :
:
![]()
Найдём коэффициент растяжения:
![]() – таким образом, в бесконечно малой окрестности точки
– таким образом, в бесконечно малой окрестности точки ![]() отображение
отображение ![]() увеличивает масштаб в 15 раз.
увеличивает масштаб в 15 раз.
Определим угол поворота:
![]() – таким образом, отображение осуществляет здесь поворот примерно на 53,1 градус по часовой стрелке.
– таким образом, отображение осуществляет здесь поворот примерно на 53,1 градус по часовой стрелке.
Пример 4. Решение: функция ![]() регулярна на всей комплексной плоскости. Найдём производную:
регулярна на всей комплексной плоскости. Найдём производную: ![]() , следовательно, отображение конформно всюду.
, следовательно, отображение конформно всюду.
Так как ![]() , то по формуле Эйлера:
, то по формуле Эйлера:
![]()
Составим функцию модуля производной:
![]()
Таким образом, коэффициент растяжения определяется функцией ![]() , и, как мы видим, от «игрека» тут ничего не зависит, можно ещё записать так:
, и, как мы видим, от «игрека» тут ничего не зависит, можно ещё записать так: ![]() .
.
Отображение не меняет масштаб, если ![]() . В нашем случае получаем уравнение
. В нашем случае получаем уравнение ![]() с очевидным решением
с очевидным решением ![]() . Таким образом, точки
. Таким образом, точки ![]() мнимой оси (их бесконечно малые окрестности) не искажаются при отображении
мнимой оси (их бесконечно малые окрестности) не искажаются при отображении ![]() .
.
Определим, где отображение растягивает плоскость. Для этого нужно решить неравенство ![]() , в нашем случае:
, в нашем случае:
![]() и этому простому неравенству удовлетворяют числа
и этому простому неравенству удовлетворяют числа ![]() с положительной действительной частью
с положительной действительной частью ![]() («игрек», как мы помним, любое).
(«игрек», как мы помним, любое).
Таким образом, отображение ![]() растягивает плоскость в области
растягивает плоскость в области ![]() (правой полуплоскости).
(правой полуплоскости).
И, очевидно, область сжатия определяется неравенством ![]() :
:
![]() , что соответствует левой полуплоскости
, что соответствует левой полуплоскости ![]() .
.
Примечание: в общем случае неравенства ![]() получаются более сложными; для их решения удобно использовать графический метод, который мы разобрали на первом уроке по ФНП (много примеров по ссылке).
получаются более сложными; для их решения удобно использовать графический метод, который мы разобрали на первом уроке по ФНП (много примеров по ссылке).
Определим множество точек, где отображение осуществляет поворот на 90 градусов:
![]() . Анализируем формулу аргумента:
. Анализируем формулу аргумента:
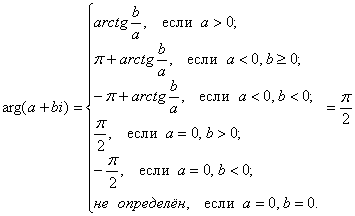
Значению ![]() соответствует случай
соответствует случай ![]() (3-я снизу строчка). В нашей задаче
(3-я снизу строчка). В нашей задаче ![]() , то есть
, то есть![]() . Таким образом, получаем систему:
. Таким образом, получаем систему:
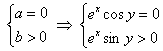 , экспонента
, экспонента ![]() при любом «икс», поэтому оба условия можно на неё сократить, имея далее в виду, что
при любом «икс», поэтому оба условия можно на неё сократить, имея далее в виду, что ![]() – любое:
– любое:
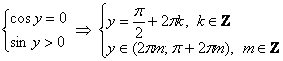
Значения ![]() входят в интервалы
входят в интервалы ![]() , а значит, являются решением системы.
, а значит, являются решением системы.
Вывод: отображение ![]() осуществляет поворот на 90 градусов в точках
осуществляет поворот на 90 градусов в точках ![]() ,
, ![]() («икс» – любое) – это прямые, параллельные действительной оси.
(«икс» – любое) – это прямые, параллельные действительной оси.
Определим множество точек, где отображение осуществляет поворот на 135 градусов:
![]() . Анализируем формулу аргумента:
. Анализируем формулу аргумента:
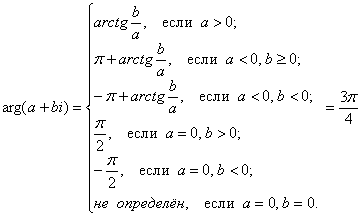
Значения с аргументом ![]() лежат во 2-й координатной четверти и подпадают под 2-ю строчку формулы. По-прежнему
лежат во 2-й координатной четверти и подпадают под 2-ю строчку формулы. По-прежнему ![]() , и сначала найдём ограничения этого случая:
, и сначала найдём ограничения этого случая:
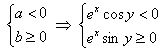 ,
, ![]() при любом
при любом ![]() , переходим к равносильной системе:
, переходим к равносильной системе:
 (пересечение интервалов)
(пересечение интервалов)
Таким образом, решением системы являются «полосы» ![]() , параллельные действительной оси (коль скоро
, параллельные действительной оси (коль скоро ![]() любое).
любое).
Теперь решаем уравнение:
![]() , в нашем случае:
, в нашем случае:
![]()
![]() (стало быть, «икс» любое)
(стало быть, «икс» любое)
![]()
и тут нельзя просто так взаимоуничтожать функции, тангенс – это периодическая функция с периодом «пи», поэтому:
![]()
теперь можно, решения потеряны не будут:
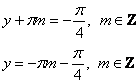
или в эквивалентной записи:
![]()
Однако условию ![]() удовлетворяют не все решения, подходит лишь половина:
удовлетворяют не все решения, подходит лишь половина: ![]()
Вывод: функция ![]() осуществляет поворот на 135 градусов в точках
осуществляет поворот на 135 градусов в точках ![]() ,
, ![]() любое.
любое.
Ответ: функция ![]() растягивает комплексную плоскость в её правой полуплоскости
растягивает комплексную плоскость в её правой полуплоскости ![]() , сжимает – в левой:
, сжимает – в левой: ![]() и оставляет неизменной в точках мнимой оси
и оставляет неизменной в точках мнимой оси ![]() . Поворачивает на 90 градусов в точках
. Поворачивает на 90 градусов в точках ![]() :
: ![]() (прямые, параллельные действительной оси) и осуществляет поворот на 135 градусов по прямым
(прямые, параллельные действительной оси) и осуществляет поворот на 135 градусов по прямым ![]() ,
, ![]() любое.
любое.
Пример 6. Решение: функция ![]() регулярна на всей комплексной плоскости, найдём производную:
регулярна на всей комплексной плоскости, найдём производную: ![]() . Отображение конформно всюду, кроме
. Отображение конформно всюду, кроме ![]() , где производная обращается в ноль, но эта точка не входит в область
, где производная обращается в ноль, но эта точка не входит в область ![]() .
.
Выделим действительную и мнимую часть производной. Так как ![]() , то:
, то:
![]()
Составим функцию модуля производной:
![]()
0) Найдём коэффициент растяжения в точке ![]() :
:
![]()
Таким образом, в бесконечно малой окрестности точки ![]() функция
функция ![]() увеличивает расстояние между отображаемыми точками в 4 раза.
увеличивает расстояние между отображаемыми точками в 4 раза.
Найдём соответствующий угол поворота:
![]() – таким образом, отображаемые объекты здесь поворачиваются на 90 градусов против часовой стрелки, что, кстати, хорошо видно по чертежу.
– таким образом, отображаемые объекты здесь поворачиваются на 90 градусов против часовой стрелки, что, кстати, хорошо видно по чертежу.
1) Найдём длину образа отрезка ![]() :
:
![]()
Отрезок ![]() лежит на прямой
лежит на прямой ![]() , следовательно,
, следовательно, ![]() – со знаком «плюс», т. к. интегрировать будем по возрастанию переменной
– со знаком «плюс», т. к. интегрировать будем по возрастанию переменной ![]() :
:
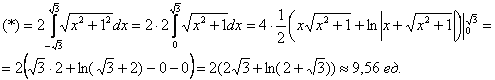
Примечание: интеграл разобран в Примере 5 статьи Сложные интегралы.
2) Найдём длину образа дуги ![]() :
:
![]()
Запишем параметрические уравнения окружности ![]() , на которой лежит дуга
, на которой лежит дуга ![]() :
: ![]() и преобразуем подынтегральную функцию:
и преобразуем подынтегральную функцию:
![]()
Найдём ![]() и составим:
и составим:
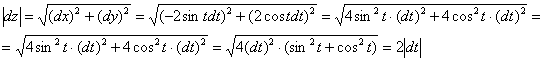
Точке ![]() соответствует следующее значение параметра:
соответствует следующее значение параметра:
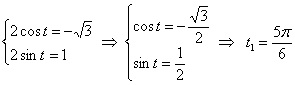 (можно определить, например, по тригонометрической таблице).
(можно определить, например, по тригонометрической таблице).
И точке ![]() , очевидно, соответствует значение
, очевидно, соответствует значение ![]() .
.
Интегрировать будем в направлении убывания параметра, поэтому ![]() :
:
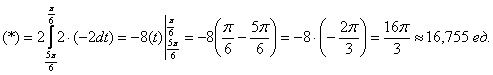
3) Вычислим площадь Пакмэна:
![]()
Перейдём к полярным координатам: ![]() .
.
![]()
Уравнение прямой ![]() в полярных координатах имеет вид
в полярных координатах имеет вид ![]() . В нашем случае:
. В нашем случае:
![]() .
.
Порядок обхода области:
![]() (от прямой до верхней полуокружности);
(от прямой до верхней полуокружности);
![]()
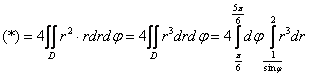
Найдём внутренний интеграл:
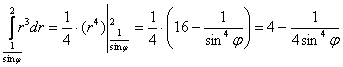
Внешний интеграл по соответствующим формулам сведём к котангенсу и его производной, заметьте, что котангенс непрерывен на промежутке интегрирования:

Ответ: 0) ![]() , 1)
, 1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright