


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
ТФКП для начинающих. Функция комплексной переменной
Не занимайтесь комплексными функциями после комплексного обеда #2
Открываем новый раздел под названием теория функции комплексной переменной (ТФКП), часто также говорят, комплексного переменного. Теории будет, как обычно, немного – больше практики, в соответствии с концепцией проекта.
Начинающим рекомендую изучать всё по порядку, к слову, вы уже далеко не «чайники», и для «самоваров» – оглавление, ибо урок задался недетский:
- комплексные числа, быстрое повторение;
- введение в ТФКП, рекомендуемая доступная литература;
- понятие функции комплексной переменной, простейшие примеры;
- комплексная экспонента;
- комплексный синус и косинус, ну и тангенс с котангенсом, вестимо;
- комплексные гиперболические функции;
- формула Эйлера;
- действительная и мнимая часть комплексной функции;
- комплексный логарифм;
- комплексная степеннАя и показательная функция;
- комплексные обратные тригонометрические функции;
- комплексные обратные гиперболические функции,
+ план дальнейшего освоения темы.
Поехали:
для изучения раздела нужно знать, что такое комплексные числа и уметь выполнять действия с ними. Но азы быстренько повторим, да и новенькая инфа сразу будет:
комплексное число – это двумерное число вида ![]() , где
, где ![]() и
и ![]() – произвольные действительные числа, а
– произвольные действительные числа, а ![]() – мнимая единица. Число
– мнимая единица. Число ![]() – это действительная часть (
– это действительная часть (![]() ) комплексного числа
) комплексного числа ![]() , число
, число ![]() – его мнимая часть (
– его мнимая часть (![]() ) .
) .
Множество комплексных чисел обозначают стилизованной, утолщённой или жирной буквой ![]() .
.
Комплексные числа изображают на комплексной плоскости, которая состоит из действительной оси, мнимой оси и начала координат:
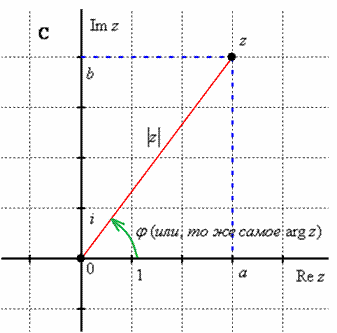
Кроме того, будем рассматривать бесконечно удалённую точку ![]() . В теории строго доказано (и показано), что она единственна – в какую бы сторону комплексной плоскости мы ни уходили, то будем приближаться к этой точке. …Ну вот и повеяло матаном :)
. В теории строго доказано (и показано), что она единственна – в какую бы сторону комплексной плоскости мы ни уходили, то будем приближаться к этой точке. …Ну вот и повеяло матаном :)
Запись ![]() называют алгебраической формой комплексного числа, но это не единственный вариант. Любое комплексное число (кроме нуля) можно представить в тригонометрической форме
называют алгебраической формой комплексного числа, но это не единственный вариант. Любое комплексное число (кроме нуля) можно представить в тригонометрической форме ![]() , где
, где ![]() – это модуль комплексного числа, а
– это модуль комплексного числа, а ![]() – его аргумент.
– его аргумент.
Модуль – это расстояние ![]() от соответствующей точки комплексной плоскости до начала координат (красный отрезок на чертеже выше), аргумент
от соответствующей точки комплексной плоскости до начала координат (красный отрезок на чертеже выше), аргумент ![]() – это угол между положительной полуосью действительной оси
– это угол между положительной полуосью действительной оси ![]() и соответствующим отрезком (зелёная стрелка).
и соответствующим отрезком (зелёная стрелка).
Если число, расположено в верхней полуплоскости либо на оси ![]() , то аргумент, очевидно, находится в пределах
, то аргумент, очевидно, находится в пределах ![]() . Если же число лежит в нижней полуплоскости, то угол принято «откручивать» по часовой стрелке и добавлять к нему знак «минус», а посему он принимает значения из интервала
. Если же число лежит в нижней полуплоскости, то угол принято «откручивать» по часовой стрелке и добавлять к нему знак «минус», а посему он принимает значения из интервала ![]() . Значение из промежутка
. Значение из промежутка ![]() называют главным значением аргумента. Ещё есть не главные, их бесконечно много. Это когда к главному «прикручиваются» обороты, так, вместо угла
называют главным значением аргумента. Ещё есть не главные, их бесконечно много. Это когда к главному «прикручиваются» обороты, так, вместо угла ![]() можно невозбранно рассмотреть
можно невозбранно рассмотреть ![]() или, например,
или, например, ![]() . Впрочем, за последний вариант бранить вас будут :)
. Впрочем, за последний вариант бранить вас будут :)
Таким образом, аргумент можно записать в виде:
![]() , где
, где ![]() принимает все целые значения
принимает все целые значения ![]() . Далее под записью
. Далее под записью ![]() будем понимать именно главное значение аргумента, когда
будем понимать именно главное значение аргумента, когда ![]() .
.
Что касаемо формул, то здесь разнообразие. И чтобы не писать слишкоммногобуков:
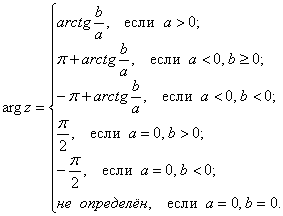
ну а с геометрией (где какие числа лежат) разберитесь самостоятельно. И выпишите, кстати, эти формулы на листочек, будет удобно в них заглядывать.
…Что ещё? Ещё вспомним понятие сопряженного комплексного числа. Числа вида ![]() ,
, ![]() называют сопряжёнными (по отношению друг к другу). Обратите внимание на чёрточку сверху второго числа – это общепринятое обозначение.
называют сопряжёнными (по отношению друг к другу). Обратите внимание на чёрточку сверху второго числа – это общепринятое обозначение.
Теперь переходим непосредственно к теме с аббревиатурой ТФКП, которую также называют комплЕксным анализом. Не ошибайтесь в ударении – это как компАсы у матросов или дОбыча у горняков, к тому же кОмплексный анализ подразумевает нечто другое, а именно всеобъемлющий анализ чего-либо.
А анализ комплЕксный – это анализ математический с его основными понятиями: функция, предел, непрерывность, производная, интеграл, ряд и др. С той поправкой, что все эти вещи рассматриваются в комплексной области.
Сейчас, когда вы читаете эти строки, на сайте представлены далеко не все темы ТФКП, поэтому я сразу приведу рекомендуемый список доступной литературы. Для наработки практики можно использовать следующие источники:
– М. Л. Краснов, А. И. Киселёв, Г. И. Макаренко - Функции комплексного переменного. Задачи и примеры с подробными решениями;
– П. Е. Данко и КО - Высшая математика в упражнениях и задачах;
– методичка Пожарского А. А. (СПбГУ) – очень обстоятельный источник с достаточно редкими темами; также мне понравились методички мехмата и КФУ.
И потребителям теории:
– И. И. Привалов - Введение в теорию функции комплексного переменного – имеет статус учебника, что дорогОго стОит;
– И. Г. Араманович, Г. Л. Лунц. Л. Э. Эльсгольц - Функции комплексного переменного. Операционное исчисление. Теория устойчивости.
+ конечно, стандартные кирпичи по матану, Бохан, Фихтенгольц и др.
Выражаю благодарность посетителям, которые порекомендовали некоторые из этих источников в тематическом посте нашего блога, кстати, загляните – найдёте массу полезной информации.
Начинаем. И начнём мы с основополагающего понятия:
функцией комплексной переменной называют правило (закон) ![]() , по которому каждому допустимому комплексному значению
, по которому каждому допустимому комплексному значению ![]() ставится в соответствие одно или бОльшее количество значений
ставится в соответствие одно или бОльшее количество значений ![]() .
.
В первом случае функцию называют однозначной, первое, что пришло в голову: ![]() , во втором – многозначной, классика жанра:
, во втором – многозначной, классика жанра: ![]() – как вы помните, корень энной степени имеет ровно «эн» корней.
– как вы помните, корень энной степени имеет ровно «эн» корней.
Рассмотрим ![]() . Очевидно, эта функция определена для всех значений
. Очевидно, эта функция определена для всех значений ![]() , и не составляет никакого труда вычислить её значение в любой точке. Так, если
, и не составляет никакого труда вычислить её значение в любой точке. Так, если ![]() , то
, то ![]() . Геометрически это изображается с помощью двух комплексных плоскостей:
. Геометрически это изображается с помощью двух комплексных плоскостей:
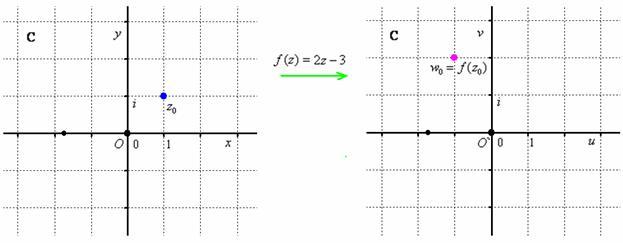
Плоскость, которая соответствует независимой переменной ![]() , обозначают
, обозначают ![]() , а плоскость, которая соответствует значениям
, а плоскость, которая соответствует значениям ![]() функции
функции ![]() – буквами
– буквами ![]() . Большие буквы тоже можно использовать:
. Большие буквы тоже можно использовать: ![]() и
и ![]() , что привычнее.
, что привычнее.
В отличие от действительной переменной, комплексная переменная ![]() не имеет определённого направления изменения, и мы можем двигаться по произвольной траектории в комплексной плоскости
не имеет определённого направления изменения, и мы можем двигаться по произвольной траектории в комплексной плоскости ![]() . При этом правило
. При этом правило ![]() разные линии плоскости
разные линии плоскости ![]() отображает в разные (в общем случае) линии плоскости
отображает в разные (в общем случае) линии плоскости ![]() . Таким образом, можно говорить о графике функции комплексной переменной. Правда, график этот специфический, у меня он ассоциируется с морозными узорами на стекле и масляными пятнами на воде. И что именно происходит – сразу понятно лишь в простых случаях, так, функция
. Таким образом, можно говорить о графике функции комплексной переменной. Правда, график этот специфический, у меня он ассоциируется с морозными узорами на стекле и масляными пятнами на воде. И что именно происходит – сразу понятно лишь в простых случаях, так, функция ![]() «вытягивает» все точки плоскости
«вытягивает» все точки плоскости ![]() в 2 раза, отображая их на плоскость
в 2 раза, отображая их на плоскость ![]() .
.
В некоторых источниках графики раскрашивают и даже строят трёхмерные модели, но мы не будем на этом останавливаться, важно, что у вас сложилось само понимание графика функции ![]() .
.
Немедленно приступаем к практике, повторяя заодно алгебраические действия с комплексными числами:
Пример 1
Вычислить значение комплексной функции в точке. Представить его в тригонометрической форме.
а) ![]() в точке
в точке ![]() ;
;
б) ![]() в точках
в точках ![]() ,
, ![]() ;
;
и давайте ещё рассмотрим такой пример:
в) ![]() в точке
в точке ![]() .
.
Решение: а) Если функция задана «иксами» / «игреками», то всё очень просто. Это не что иное, как действительная и мнимая часть независимой переменной ![]() . В нашем случае
. В нашем случае ![]() , стало быть
, стало быть ![]() , и соответствующее значение функции:
, и соответствующее значение функции:
![]()
Представим результат в тригонометрической форме. Для этого нужно найти его модуль:
![]()
и аргумент, поскольку ![]() , то (см. формулы выше):
, то (см. формулы выше):
![]()
Таким образом, ![]() .
.
И следующие пункты более распространены:
б) если функция задана непосредственно через «зет», то выполняем обычные действия, главное, помнить знаменитый квадрат ![]() и быть внимательным:
и быть внимательным:
Вычислим значение функции ![]() в точке
в точке ![]() , используем формулу
, используем формулу ![]() :
:
![]()
Вычислим значение той же функции в точке ![]() :
:
![]()
Представим полученные значения в тригонометрической форме. Найдём модуль и аргумент числа ![]() :
:
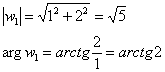
Таким образом, ![]() .
.
Теперь обратим внимание на следующую вещь: значения ![]() ,
, ![]() получились сопряжёнными, а у таких чисел модули равны, а аргументы – противоположны по знаку. Сиё следует из элементарной геометрии.
получились сопряжёнными, а у таких чисел модули равны, а аргументы – противоположны по знаку. Сиё следует из элементарной геометрии.
Поэтому ![]() .
.
Напоминаю, что знак «минус» под косинусом ни в коем случае убирать нельзя (пользуясь чётностью косинуса). Минус из-под синуса тоже выносить не нужно. Если аргумент отрицателен, то записываем его именно так, как записано в этом примере.
в) Вычислим значение функции ![]() в точке
в точке ![]() :
:
![]()
Используем стандартный приём. Чтобы избавить от мнимой единицы на нижнем этаже, умножим числитель и знаменатель на сопряжённое знаменателю число, дабы воспользоваться формулой ![]() :
:
![]() , модуль и аргумент находить не хочется.
, модуль и аргумент находить не хочется.
А вот на счёт самой функции ![]() есть что сказать. Как вы прочувствовали, с комплексными числами можно делать многое, но на ноль всё-таки делить нельзя :) Поэтому данная функция определена для всех «зет», кроме
есть что сказать. Как вы прочувствовали, с комплексными числами можно делать многое, но на ноль всё-таки делить нельзя :) Поэтому данная функция определена для всех «зет», кроме ![]() . Запишем этот факт с помощью стандартного значка области определения функции:
. Запишем этот факт с помощью стандартного значка области определения функции: ![]() – все комплексные числа кроме нуля.
– все комплексные числа кроме нуля.
Таким образом, для комплексной функции в ходу те же понятия области определения ![]() и области значений
и области значений ![]() функции.
функции.
Тренируемся самостоятельно – в лучших традициях я предлагаю самые интересные задания:
Пример 2
Вычислить значение комплексной функции в точке, найти его модуль и аргумент:
а) ![]() в точках
в точках ![]() ;
;
б) ![]() в точке
в точке ![]()
Решения и ответы в конце урока.
Хорошо, то были наиболее простые функции. Но как быть с экспонентой, логарифмом, синусом, косинусом и иже с ними функциями? Существуют ли они в комплексной области? Да, существуют! Правда, теряют «действительный» («школьный») смысл.
Комплексная экспонента – есть сумма функционального ряда:
![]() – знакомая картинка, только раньше мы имели дело с действительной экспонентой («е в степени икс»), и теперь пришло время обобщить её на комплексный случай
– знакомая картинка, только раньше мы имели дело с действительной экспонентой («е в степени икс»), и теперь пришло время обобщить её на комплексный случай
Этот ряд сходится абсолютно к ![]() на всей комплексной плоскости (при любом конечном значении «зет».). О понятии сходимости ряда я рассказал, когда мы раскладывали в ряды действительные функции, но повторюсь и сейчас. Рассмотрим произвольное конечное «зет», например,
на всей комплексной плоскости (при любом конечном значении «зет».). О понятии сходимости ряда я рассказал, когда мы раскладывали в ряды действительные функции, но повторюсь и сейчас. Рассмотрим произвольное конечное «зет», например, ![]() . Если мы возьмём несколько первых членов ряда, скажем, три, то получим очень грубое приближение соответствующего значения экспоненты:
. Если мы возьмём несколько первых членов ряда, скажем, три, то получим очень грубое приближение соответствующего значения экспоненты: ![]() Если членов взять больше, например, пять, то сумма
Если членов взять больше, например, пять, то сумма ![]() (тоже конкретное число) уже будет лучше приближать истинное значение
(тоже конкретное число) уже будет лучше приближать истинное значение ![]() . И чем больше членов – тем точнее приближение. И, наконец, бесконечная сумма
. И чем больше членов – тем точнее приближение. И, наконец, бесконечная сумма ![]() – в точности равна
– в точности равна ![]() . Обращаю внимание, что значение
. Обращаю внимание, что значение ![]() не «летает где-то в воздухе» – ему соответствует определённая точка комплексной плоскости, и чуть позже мы представим это число в алгебраической форме
не «летает где-то в воздухе» – ему соответствует определённая точка комплексной плоскости, и чуть позже мы представим это число в алгебраической форме ![]() .
.
Для комплексной экспоненты справедливы привычные свойства ![]() , и, кроме того, эта функция периодическая (да, вот такая неожиданность) с мнимым периодом
, и, кроме того, эта функция периодическая (да, вот такая неожиданность) с мнимым периодом ![]() , то есть справедливо равенство
, то есть справедливо равенство ![]() , где
, где ![]() («ка» принимает все целые значения).
(«ка» принимает все целые значения).
Комплексные синус и косинус – есть суммы следующих рядов:
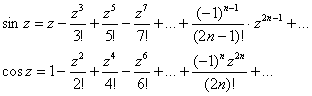
которые абсолютно сходятся тоже на всей комплексной плоскости.
Это функции периодичные с привычным действительным периодом ![]() и нулями
и нулями ![]() для синуса и
для синуса и ![]() для косинуса. Однако комплексные синус с косинусом могут приниматься любые значения, в том числе действительные, причём бОльшие единицы, поэтому что-то вроде
для косинуса. Однако комплексные синус с косинусом могут приниматься любые значения, в том числе действительные, причём бОльшие единицы, поэтому что-то вроде ![]() – обычное себе дело.
– обычное себе дело.
Для комплексных тригонометрических функций справедливы все «действительные» тригонометрические формулы, в частности, ![]() .
.
Особое место в комплексном анализе занимают гиперболические функции, которые до сих пор оставались в тени. Гиперболический синус:
![]()
и гиперболический косинус:
![]()
Эти ряды элементарно получаются из разложения экспоненты для ![]() и для
и для ![]() , и желающие могут вывести их самостоятельно. Гиперболический тангенс с котангенсом определяются аналогично:
, и желающие могут вывести их самостоятельно. Гиперболический тангенс с котангенсом определяются аналогично: ![]() . Для комплексных гиперболиков справедливы «действительные» формулы, самая известная из них – основное гиперболическое тождество:
. Для комплексных гиперболиков справедливы «действительные» формулы, самая известная из них – основное гиперболическое тождество: ![]() .
.
Преобразуя соответствующие ряды, несложно выразить комплексный синус и косинус через экспоненту: ![]() , откуда следует их взаимосвязь с гиперболическими собратьями:
, откуда следует их взаимосвязь с гиперболическими собратьями: ![]() , ну или так можно записать:
, ну или так можно записать: ![]() .
.
Из разложений экспоненты, синуса и косинуса следует* важнейшая, я бы даже сказал одна из ключевых – формула Эйлера:
![]() , где
, где ![]() – произвольное действительное число.
– произвольное действительное число.
* Самостоятельно подставьте ![]() в разложение экспоненты и получИте формулу.
в разложение экспоненты и получИте формулу.
В частности, если ![]() – аргумент комплексного числа
– аргумент комплексного числа ![]() , то мы можем записать его не только в тригонометрической
, то мы можем записать его не только в тригонометрической ![]() , но ещё и в показательной форме
, но ещё и в показательной форме ![]() . Таким образом, показательная форма комплексного числа – это не какая-то «надуманная» конструкция, а строгая вещь, основанная на формуле Эйлера.
. Таким образом, показательная форма комплексного числа – это не какая-то «надуманная» конструкция, а строгая вещь, основанная на формуле Эйлера.
Известнейший частный случай формулы соответствует значению ![]() :
:
![]()
![]() – в результате чего получается экзистенциальное тождество, связывающее пять фундаментальных констант: ноль, единицу, «е», «пи» и «и». Этот факт приводил в восторг многих математиков, и мы с воодушевлением продолжаем тему.
– в результате чего получается экзистенциальное тождество, связывающее пять фундаментальных констант: ноль, единицу, «е», «пи» и «и». Этот факт приводил в восторг многих математиков, и мы с воодушевлением продолжаем тему.
С помощью формулы Эйлера легко представить в алгебраической форме любое значение экспоненты. Если ![]() – произвольное комплексное число, то:
– произвольное комплексное число, то:
![]()
В частности, для ![]() имеем:
имеем:
![]() – число
– число ![]() в алгебраической форме. Значения
в алгебраической форме. Значения ![]() и
и ![]() получились «плохими» (но конкретными!), поэтому так и оставляем.
получились «плохими» (но конкретными!), поэтому так и оставляем.
Синус и косинус комплексного значения ![]() тоже можно представить в алгебраической форме, формулы приведу без вывода:
тоже можно представить в алгебраической форме, формулы приведу без вывода:
![]()
Так, для того же значения ![]() :
:
![]()
Ради исследовательского интереса проверьте формулы для произвольного действительного «зет», например, ![]() (учитывая, что
(учитывая, что ![]() ).
).
Эти три формулы (экспоненты, синуса, косинуса) перепишите себе на листок – будут постоянно требоваться на практике. Напомню также выражения ![]() , с помощью которых можно перейти от гиперболиков к «обычному» синусу и косинусу, ну а их формулы только что были выше.
, с помощью которых можно перейти от гиперболиков к «обычному» синусу и косинусу, ну а их формулы только что были выше.
Продолжаем:
Пример 3
а) вычислить значение функции ![]() в точке
в точке ![]() , результат представить в алгебраической форме;
, результат представить в алгебраической форме;
б) Записать число ![]() в алгебраической форме;
в алгебраической форме;
в) …нет, маньячить не будем, решаем:
а) Вычислим значение функции ![]() в точке
в точке ![]() :
:
![]()
используем формулу ![]() :
:
![]()
б) Используем формулу ![]() :
:
![]()
И творческие примеры для самостоятельного решения:
Пример 4
а) решить уравнение ![]() (используйте запись
(используйте запись ![]() );
);
б) представить в алгебраической форме число ![]() (формула есть выше!).
(формула есть выше!).
Сверяемся и продолжаем.
До сих пор мы находили значения функций «вручную», и возникает вопрос: а нельзя ли усовершенствовать процесс, чтобы сразу подставлять «икс» и «игрек» из ![]() в функцию и получать результаты? Конечно, можно! И нужно, ведь это удобно.
в функцию и получать результаты? Конечно, можно! И нужно, ведь это удобно.
Функцию ![]() можно представить в виде
можно представить в виде ![]() , где
, где ![]() и
и ![]() – это функции двух действительных переменных, которым посвящен целый раздел сайта. При этом функцию
– это функции двух действительных переменных, которым посвящен целый раздел сайта. При этом функцию ![]() называют действительной частью функции
называют действительной частью функции ![]() , а
, а ![]() – её мнимой частью.
– её мнимой частью.
Пример 5
Найти действительную и мнимую части функций, возьмём те, которые уже были:
а) ![]() ;
;
б) ![]() .
.
Решение: а) поскольку ![]() , то:
, то:
![]()
теперь нужно перегруппировать слагаемые – сначала записать те, в которых нет мнимой единицы, а потом те – где она есть, после чего вынести «и» за скобку:
![]()
Таким образом, ![]() действительная часть функции
действительная часть функции ![]() , а
, а ![]() – её мнимая часть.
– её мнимая часть.
Как я уже отметил, запись ![]() удобно использовать для расчёта конкретных значений функции, например, в точке
удобно использовать для расчёта конкретных значений функции, например, в точке ![]() . Распишу очень подробно, хотя на самом деле вычисления здесь устные:
. Распишу очень подробно, хотя на самом деле вычисления здесь устные:
![]()
Что и говорить, это гораздо удобнее, чем подставлять ![]() непосредственно в
непосредственно в ![]() . А если точек много, то без формы
. А если точек много, то без формы ![]() обойтись вообще практически невозможно.
обойтись вообще практически невозможно.
б) Поскольку ![]() , то:
, то:
![]()
используем формулу Эйлера ![]() :
:
![]()
Таким образом, ![]() – действительная часть функции
– действительная часть функции ![]() , а
, а ![]() – её мнимая часть.
– её мнимая часть.
Самостоятельно:
Пример 6
Определить действительную и мнимую часть функций:
а) ![]() , формула куба суммы в помощь;
, формула куба суммы в помощь;
б) ![]() ;
;
в) ![]() .
.
Этого пока достаточно, ещё успеется много раз :)
И во второй части нашего увлекательного урока кратко познакомимся с другими функциями.
Комплексный логарифм ![]() определяется как функция, обратная к экспоненциальной, опуская выкладки:
определяется как функция, обратная к экспоненциальной, опуская выкладки:
![]() , где
, где ![]() («ка» принимает все целые значения), при этом
(«ка» принимает все целые значения), при этом ![]() называют главным значением логарифма, оно получается при
называют главным значением логарифма, оно получается при ![]() и представИмо в алгебраической форме следующим образом:
и представИмо в алгебраической форме следующим образом:
![]()
Таким образом, логарифм можно расписать так:
![]() , где
, где ![]() .
.
Как видите, это многозначная функция, а точнее бесконечнозначная – каждому ненулевому значению «зет» соответствует бесконечно много значений «дубльвэ».
Для комплексного логарифма справедливы привычные формулы:
![]()
и не очень привычная:
![]() , где
, где ![]() – произвольное комплексное число.
– произвольное комплексное число.
Пример 7
Вычислить значения функции ![]() в точке
в точке ![]() .
.
Решение: запишем функцию в виде ![]() и вычислим её значения в точке
и вычислим её значения в точке ![]() :
:
![]() и давайте сразу разберёмся, что здесь к чему.
и давайте сразу разберёмся, что здесь к чему.
А ситуация следующая: значению ![]() соответствует бесконечно много значений логарифма
соответствует бесконечно много значений логарифма ![]() , прежде всего, это его главное значение
, прежде всего, это его главное значение ![]() (при
(при ![]() ) и остальные значения
) и остальные значения ![]() . Можно ещё записать так:
. Можно ещё записать так:
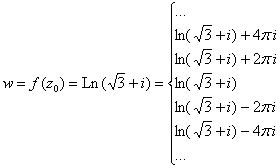
Представим главное значение логарифма в алгебраической форме по формуле ![]() . Для этого найдём модуль и аргумент числа
. Для этого найдём модуль и аргумент числа ![]() :
:
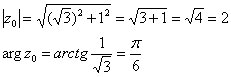
Таким образом:
![]() , где
, где ![]() – значения логарифма
– значения логарифма ![]() в алгебраической форме.
в алгебраической форме.
Пример 8
Вычислить ![]() и
и ![]() .
.
Быстренько решаем самостоятельно и переходим к другим функциям.
Общая степеннАя функция ![]() , где
, где ![]() – произвольное комплексное число, определяется с помощью основного логарифмического тождества, справедливого и в комплексном случае:
– произвольное комплексное число, определяется с помощью основного логарифмического тождества, справедливого и в комплексном случае:
![]()
Очевидно, эта функция многозначна, и её главное значение соответствует главному значению логарифма: ![]() .
.
Общая показательная функция ![]() , где
, где ![]() определяется аналогично:
определяется аналогично:
![]() и имеет главное значение
и имеет главное значение ![]() .
.
Рассмотрим «классические» примеры:
Пример 9
а) вычислить значения функции ![]() в точке
в точке ![]() ;
;
б) вычислить ![]() .
.
Решение: а) если ![]() , то значения степеннОй функции
, то значения степеннОй функции ![]() таковы:
таковы:
![]()
Значения ![]() только что были найдены в Примере 8:
только что были найдены в Примере 8:
![]() ,
, ![]() – таким образом, «и» в степени «и», оказывается, равно бесконечному количеству действительных значений.
– таким образом, «и» в степени «и», оказывается, равно бесконечному количеству действительных значений.
б) Логарифм ![]() можно вычислить двумя способами.
можно вычислить двумя способами.
1) Непосредственно по определению:
![]()
Поскольку (см. предыдущий пункт) ![]() для всех
для всех ![]() , то все эти числа расположены на действительной положительной полуоси
, то все эти числа расположены на действительной положительной полуоси ![]() , а значит, их модули:
, а значит, их модули: 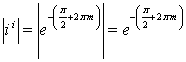 , а аргумент
, а аргумент ![]() . Таким образом:
. Таким образом:
![]() , где
, где ![]() .
.
Что это за конструкция? Здесь каждому целому значению «эм» соответствует бесконечно много целых значений «ка». Вот такое вот получилось множество значений ![]() .
.
2) Вычислим этот логарифм с помощью свойства ![]() :
:
![]()
ну а логарифм «и» был найден в Примере 8:
![]() , где
, где ![]() .
.
Пара примеров для самострельного решения:
Пример 10
а) записать в алгебраической форме ![]() ;
;
б) вычислить ![]() ;
;
в) найти значения функции ![]() в точке
в точке ![]() .
.
Результаты представить в алгебраической форме (формула Эйлера в помощь).
И на посошок арки. Обратные тригонометрические функции в комплексной области определяются как функции, обратные к ![]() , и выражаются через комплексный логарифм:
, и выражаются через комплексный логарифм:
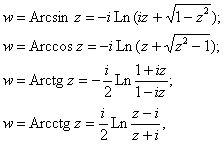
при этом в разных источниках вы можете встретить несколько разные формулы для арктангенса и арккотангенса (кстати, не путайте их по невнимательности).
Эти функции многозначны (ибо логарифм) и их главные части, обозначаемые ![]() ,
, ![]() ,
, ![]() ,
, ![]() , соответствуют главному значению логарифма.
, соответствуют главному значению логарифма.
Решим эпичное уравнение:
Пример 11
![]()
Решение: поскольку ![]() , то обратные значения:
, то обратные значения:
![]()
Используем формулу ![]() , здесь, чтобы не возникло «накладок» с обозначениями вместо «зет» я использовал букву «тэ»:
, здесь, чтобы не возникло «накладок» с обозначениями вместо «зет» я использовал букву «тэ»:
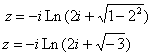
квадратный корень имеет два значения, поэтому получаем две ветки решений:
![]() и
и ![]()
1) Найдём значения ![]()
Поскольку число ![]() лежит на мнимой оси, причём выше нуля, то:
лежит на мнимой оси, причём выше нуля, то:
![]()
Таким образом:
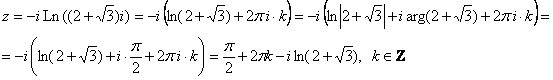
2) И со значениями ![]() почти всё так же:
почти всё так же:
![]() (обратите внимание, что
(обратите внимание, что ![]() тоже больше нуля и число
тоже больше нуля и число ![]() лежит на мнимой оси – тоже в верхней полуплоскости).
лежит на мнимой оси – тоже в верхней полуплоскости).
и в результате получаем:
![]()
Обе ветки решения можно записать единой строкой, используя значок «плюс-минус»:
ответ: ![]() – корни уравнения
– корни уравнения ![]() .
.
И фантазии В. Ф. Чудесенко для самостоятельного решения:
Пример 12
Представить 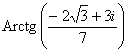 в алгебраической форме.
в алгебраической форме.
Образец для сверки внизу страницу. И для справки приведу формулы обратных гиперболических функций, их творчески можно назвать ареаболиками :) Они взаимосвязаны с арками тригонометрических функций следующим образом:
ареасинус: ![]() ;
;
ареакосинус: ![]() ;
;
ареатангенс: ![]() ;
;
ареакотангенс: ![]() .
.
Ну а арки в свою очередь выражаются через логарифм. Таким образом, если вам дано что-то вроде ![]() , то сначала переходим к соответствующему арку:
, то сначала переходим к соответствующему арку:
![]() , а затем – к логарифму, формулы там недалеко вверху были.
, а затем – к логарифму, формулы там недалеко вверху были.
На этом первое занятие подошло к концу, хотелось короче, но получилось как всегда :) Далее по курсу разберём:
– Области на комплексной плоскости – важнейший материал, нужный во многих темах;
– Линии на комплексной плоскости. Параметрический вид;
– Отображение линий и областей с помощью комплексной функций;
– Предел и непрерывность комплексной функции;
– Производная функции комплексной переменной;
– Как найти функцию по известной действительной или мнимой части?
– Конформное отображение. Смысл производной
…
(продолжение следует)
Желаю успехов!
Решения и ответы:
Пример 2. Решение: а) вычислим значение функции ![]() в точке
в точке ![]() :
:
![]()
Вычислим значение функции в точке ![]() :
:
![]()
Модуль обоих значений равен нулю, аргумент – не определён.
Примечание: значение ![]() является корнем многочленного уравнения
является корнем многочленного уравнения ![]() . Из основной теоремы алгебры следует, что коль скоро так, то и сопряженное комплексное число (
. Из основной теоремы алгебры следует, что коль скоро так, то и сопряженное комплексное число (![]() в нашем примере) тоже обязательно является корнем этого уравнения.
в нашем примере) тоже обязательно является корнем этого уравнения.
б) Вычислим значение ![]() в точке
в точке ![]() :
:
![]()
Чтобы избавиться от мнимой единицы в знаменателе домножим числитель и знаменатель на оную:
![]()
Найдём модуль и аргумент полученного значения:
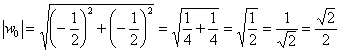
так как ![]() , то по соответствующей формуле:
, то по соответствующей формуле:
![]() .
.
Пример 4. Решение: а) поскольку ![]() , то:
, то:
![]()
используем формулу Эйлера ![]() :
:
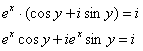
Два комплексных числа равны, если равны их действительные и мнимые части, таким образом, получаем систему:
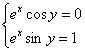
Так как ![]() , то первое уравнение обращается в ноль, только если
, то первое уравнение обращается в ноль, только если ![]() , следовательно,
, следовательно, ![]() . Синус же в этих точках равен либо +1, либо –1:
. Синус же в этих точках равен либо +1, либо –1:
![]() , тогда из второго уравнения получаем
, тогда из второго уравнения получаем ![]() ;
;
![]() , тогда из второго уравнения получаем
, тогда из второго уравнения получаем ![]() – не имеет решений (так как
– не имеет решений (так как ![]() – действительное число).
– действительное число).
Стало быть, корни уравнения: ![]() .
.
Ответ: уравнение ![]() имеет бесконечно много корней:
имеет бесконечно много корней: ![]() .
.
б) Используем формулу ![]() :
:
![]()
используем формулу ![]() :
:
![]()
Пример 6. Решение: а) так как ![]() , то:
, то:
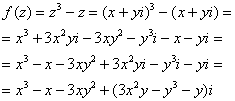
Таким образом, ![]() – действительная часть функции, а
– действительная часть функции, а ![]() – её мнимая часть.
– её мнимая часть.
б) Так как ![]() , то:
, то:
![]()
используем формулу ![]() :
:
![]()
Таким образом, ![]() – действительная часть функции,
– действительная часть функции, ![]() – её мнимая часть.
– её мнимая часть.
в) Так как ![]() , то:
, то:
![]()
Умножим числитель и знаменатель на сопряженное знаменателю число:
![]()
Таким образом, ![]() .
.
Пример 8. Решение:
![]() ,
, ![]()
![]() ,
, ![]()
Пример 10. Решение: а) Используем основное логарифмическое тождество:
![]()
б) Используем основное логарифмическое тождество:
![]()
по определению логарифма, ![]() , таким образом:
, таким образом:
![]()
используем формулу Эйлера ![]() :
:
![]() , где
, где ![]() .
.
в) ![]()
Найдём модуль и аргумент числа ![]() :
:
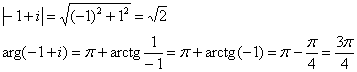
По определению логарифма:
![]()
Таким образом:
![]()
используем формулу Эйлера ![]() :
:
![]() – значения
– значения ![]() в алгебраической форме.
в алгебраической форме.
Пример 12. Решение: используем формулу ![]() . В данном случае
. В данном случае ![]() и вычисления удобно провести по пунктам:
и вычисления удобно провести по пунктам:
1) ![]() ;
;
2) ![]() ;
;
3) 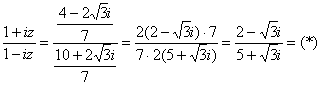
умножим числитель и знаменатель на сопряженное знаменателю число:
![]() .
.
4) Найдём модуль и аргумент числа ![]() :
:
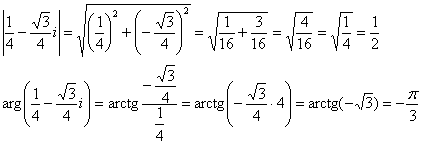
5) Таким образом:
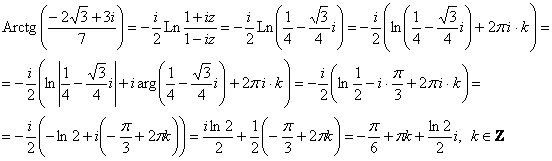
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright