Карта сайта

8. Статистические оценки параметров генеральной совокупности.
Доверительный интервал и доверительная вероятность


Вспомним первый урок по теме (там же внизу оглавление) и основной метод математической статистики. Он состоит в том, что для изучения генеральной совокупности объёма  из неё производится выборка, состоящая из  элементов, которая хорошо характеризует всю совокупность (свойство представительности). И на основании исследования этой выборочной совокупности мы с высокой достоверностью можем оценить генеральные  характеристики. Чаще всего требуется выявить закон распределения генеральной совокупности (о чём пойдёт речь позже) и оценить его важнейшие числовые параметры, такие как генеральная средняя , генеральная дисперсия  и среднее квадратическое отклонение .

Очевидно, что для оценки этих параметров нужно вычислить соответствующие выборочные значения. Так, выборочная средняя  позволяет нам оценить генеральную среднюю , причём, оценить её точечно. Почему точечно? Потому что  – это отдельно взятое, конкретное значение. Если из той же генеральной совокупности мы будем проводить многократные выборки, то в общем случае у нас будут получаться различные выборочные средние, и каждая из них представляет собой точечную оценку генерального значения .

Аналогично, несмещённой точечной оценкой генеральной дисперсии  является исправленная выборочная дисперсия , и соответственно, стандартного отклонения  – исправленное стандартное отклонение .

…что-то не понятно / недопонятно в терминах? Срочно изучать предыдущие уроки!

Недостаток точечных оценок состоит в том, что при небольшом объёме выборки (как оно часто бывает), мы можем получать выборочные значения, которые далеки от истины.
И в этих случаях логично потребовать, чтобы выборочная характеристика  (средняя, дисперсия или какая-то другая) отличалась от генерального значения  не более чем на некоторое положительное значение . А точнее, менее.

Справка:  – греческая буква «тета»,  – греческая буква «дельта».

Значение  называется точностью оценки, и озвученное выше требование можно записать с помощью модуля:

Обозначение: точность оценки также обозначают через  («эпсилон»).

Но статистические методы не позволяют 100%-но утверждать, что рассчитанное значение  будет удовлетворять этому неравенству – ведь в статистике всегда есть место случайности, когда мы можем «выиграть в лотерею» в плохом смысле этого слова. Таким образом, можно говорить лишь о вероятности , с которой это неравенство осуществится: .

А теперь я раскрою модуль:

и сформулирую суть:

Интервал  называется доверительным интервалом и представляет собой интервальную оценку генерального значения  по найденному выборочному значению . Данный интервал с вероятностью  «накрывает» истинное значение . Эта вероятность называется доверительной вероятностью или надёжностью интервальной оценки

Надёжность «гамма» часто задаётся наперёд, популярные варианты

На данном уроке будут рассмотрены:

Доверительный интервал для оценки генеральной средней
нормально распределённой генеральной совокупности

И мы сразу разберём распространённую и «заезженную» задачу, которую предлагают даже студентам-гуманитариям:

Пример 21

…да-да, пример уже 21-й!

Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением . Найти доверительный интервал для оценки математического ожидания   с надежностью 0,95, если выборочная средняя , а объем выборки .

Внимание! Важное замечание: если в задаче указан тип выборки (повторная / бесповторная), то решение будет иметь свои особенности – читайте 10-ю статью об оценках по повторной и бесповторной выборке.

А теперь принципиальный момент непосредственно по задаче:

здесь известно стандартное отклонение 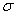 генеральной совокупности.

Дело в том, что в похожих задачах оно бывает не известно, и тогда решение будет отличаться!

Но сейчас решение таково, разбираемся в ситуации:

– из генеральной совокупности попугаев проведена выборка в  особей и по её результатам найдена выборочная средняя:  (средняя масса попугая, например).

Выборочная средняя – это точечная оценка неизвестной нам генеральной средней . Как отмечалось выше, недостаток точечной оценки состоит в том, что она может  оказаться далёкой от истины. И по условию, требуется найти интервал , которой с вероятностью  накроет истинное значение .

Именно так! Здесь будет неверным сказать, что  попадёт в этот интервал.

Решаем. Точность оценки рассчитывается по формуле , где  – коэффициент доверия. Этот коэффициент отыскивается из соотношения , где  – функция Лапласа.

В данном случае , следовательно:

И по таблице значений функции Лапласа либо пользуясь расчётным макетом (пункт 5*), выясняем, что значению   соответствует аргумент .

Таким образом, точность оценки:

и искомый доверительный интервал:

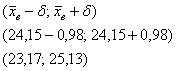
Этот интервал с вероятностью   (надёжностью) накрывает истинное генеральное значение  среднего веса попугая. Но всё же остаётся 5%-ная вероятность, что генеральная средняя окажется вне найденного интервала.

Ответ: .

И тут возникает светлая мысль уменьшить этот интервал – чтобы получить более точную оценку. Что для этого можно сделать? Давайте посмотрим на формулу .

Очевидно, что чем меньше стандартное отклонение (мера разброса значений), тем короче доверительный интервал. Но это в отдельно взятой задаче ни на что не влияет – ведь нам известно конкретное значение , и изменить его нельзя.

Поэтому для уменьшения «дельты» можно уменьшить коэффициент доверия, например, вместо  рассмотреть  и тогда: , и доверительный интервал  действительно станет в 2 раза короче. Но засада в том, что упадёт и доверительная вероятность:

, то есть о том, что этот более узкий интервал накроет генеральную среднюю, мы теперь можем утверждать лишь с вероятностью 68,26%. Что, конечно, неудовлетворительно, для серьёзного статистического исследования.

Поэтому для уменьшения доверительного интервала (при том же значении ) остаётся увеличивать объём выборки . Что совершенно понятно и без формулы , ведь чем больше объём выборки, тем точнее она характеризует генеральную совокупность (при прочих равных условиях). Об объёме мы поговорим на уроке об оценках по повторной и бесповторной выборке, ну а пока продолжаем.

Творческая задача для самостоятельного решения:

Пример 22

По результатам выборочного исследования  объектов найдена выборочная средняя .

1) С какой вероятностью можно утверждать, что генеральная средняя отличается от найденного значения менее чем на 3, если известно, что генеральная совокупность распределения нормально с дисперсией 400?

2) Определить доверительный интервал, который с надежностью  накроет истинное значение генеральной средней.

Расчётный макет (пункты 5 и 5*) – в помощь. Краткое решение в конце урока.

И тут, наверное, у вас назрели вопросы – а откуда известно, что генеральная совокупность распределена нормально, и тем более, откуда известно её стандартное отклонение?

Обычно эта информация известна из предыдущих исследований. Классический пример – измерительный прибор. Очевидно, что его случайные погрешности удовлетворяют условию теоремы Ляпунова, а значит, распределены нормально. Кроме того, производитель, как правило, тестирует прибор, и указывает в его паспорте стандартное отклонение случайных погрешностей измерений, которое можно принять за .

Но если установить нормальность распределения достаточно просто (в том числе статистическими методами), то с генеральным значением  всё сложнее – зачастую вычислить его трудно или невозможно.

В такой ситуации остаётся ориентироваться на исправленное стандартное отклонение , и решение несколько изменится. Ещё одна классическая задача, которая уже встретилась ранее:

Пример 23

В результате 10 независимых измерений некоторой величины , выполненных с одинаковой точностью, полученные опытные данные, которые представлены в таблице:

Предполагая, что результаты измерений подчинены нормальному закону распределения вероятностей, оценить истинное значение величины  при помощи доверительного интервала, покрывающего это значение с доверительной вероятностью 0,95.

Не путать со случайными ошибками измерительного прибора! Здесь речь идёт об измерениях и помимо технических, велико влияние других, в частности, человеческого фактора, особенно, если  вы используете махрово-аналоговый прибор – что-нибудь вроде механического секундомера или линейки.

Решение следует начать с вычисления выборочных характеристик, и задача облегчается тем, что в Примере 13 они уже вычислены:  и . По условию, требуется оценить генеральную совокупность (а именно, параметр ), и поэтому дисперсию нужно обязательно поправить:
 – несмещённая оценка неизвестной генеральной дисперсии . И нас будет интересовать несмещённая оценка генерального стандартного отклонения :

 – исправленное среднее квадратическое отклонение.

Теперь построим доверительный интервал для оценки истинного (генерального) значения  величины .

Если генеральное стандартное отклонение 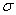не известно

(наш случай), то этот интервал строится по похожей формуле:

, с той поправкой, что коэффициент доверия  рассчитывается с помощью распределения Стьюдента. В рамках курса теорвера я не рассказывал об этом распределении, и поэтому ограничусь технической стороной вопроса.

Значение   можно найти с помощью таблицы значений распределения Стьюдента, в частности, популярна таблица, специально адаптированная для данной задачи*. И, согласно этой таблице, доверительной вероятности  и объёму выборки  соответствует коэффициент доверия:

* В стандартной же таблице приводятся значения для так называемого уровня значимости  и числа степеней свободы .

Другой, более универсальный способ – воспользоваться калькулятором, и чтобы далеко не ходить, я добавил этот функционал в расчётный макет: ищем Пункт 10б, забиваем значения  ,  и получаем «на выходе» .

Вычислим точность оценки:

Таким образом, искомый доверительный интервал:

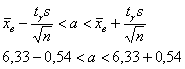
 – данный интервал с вероятностью  накрывает истинное значение  измеряемой величины .

Ответ:

Для самостоятельного решения:

Пример 24

На основании  испытаний установлено, что в среднем для изготовления шавермы полупроводникового диода требуется  секунд, а исправленное среднее квадратическое отклонение составляет  секунд. Предположив, что время изготовления диода есть нормальная случайная величина, определить с надежностью  доверительный интервал для оценки среднего времени изготовления диода

Краткое решение и ответ в конце урока – расчётный макет (Пункт 10б) – в помощь.

Итак, что главное в разобранных задачах? Главное, обратить внимание, генеральное ли нам дано отклонение  или исправленное выборочное . От этого зависит, какую формулу нужно использовать, эту:
, где ,
или эту:
, где  отыскивается с помощью распределения Стьюдента.

Некоторые коварные авторы (вроде меня) могут предложить и «простое» выборочное отклонение , и тогда его следует поправить по формуле: , которая следует из соотношения дисперсий: .  Иногда бывает предложена и дисперсия (та или иная). И поэтому именно здесь нужно проявить аккуратность, сами же вычисления достаточно примитивны.

И ещё один момент: при увеличении объёма выборки , распределение Стьюдента стремится к нормальному распределению, и поэтому уже при  (2-й случай) допускается нахождение  с помощью того же соотношения . Но я бы не рекомендовал так делать. Потому что если дано , то предполагается, что решать нужно именно через «Стьюдента», и при наличии Экселя с этим никаких проблем – можно рассчитать любые значения, которые отсутствуют в таблицах.

И быстренько более редкая задача:

Доверительный интервал для оценки
генеральной дисперсии и стандартного отклонения

Этот интервал можно построить несколькими способами, которые я постараюсь уместить буквально в пару экранов. И сейчас последует продолжение той же задачи об измерениях:

Пример 25

По  равноточным измерениям найдено исправленное среднее квадратическое отклонение . Предполагая, что результаты измерений распределены нормально, построить доверительный интервал для оценки истинного значения  (генерального стандартного отклонения) с надёжностью .

Обратите внимание, что для решения этой задачи нам не обязательно знать выборочную среднюю (хотя в Примере 23 мы её нашли).

Способ первый. Доверительный интервал для оценки неизвестной дисперсии  нормально распределённой генеральной совокупности определяется следующим образом (не пугаемся):
, где  – распределение «хи-квадрат» (ещё один скелет в шкафу:)), а ,  – его критические значения, вычисленные для ,

Данный интервал с вероятностью  (надёжностью) накрывает истинное значение . И если из всех частей неравенства извлечь корни, то получим соответствующий интервал для оценки генерального стандартного отклонения:

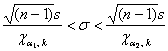
Значения  известны, и осталось разобраться с нижним этажом. Во-первых, вычислим:

и теперь, по таблице критических значений распределения  или с помощью расчётного макета (Пункт 11б) находим:

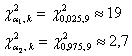
Обратите внимание, что получены различные значения, и наш доверительный интервал будет асимметричным (ввиду асимметрии распределения «хи-квадрат»):
 – не забываем извлечь корни из знаменателей!
– таким образом, с вероятностью  можно утверждать, что данный интервал накроет генеральное стандартное отклонение .

Как видите, интервал асимметричен относительно выборочного значения , и его широкий диапазон объясним малым объёмом выборки – велика вероятность, что при 10 измерениях полученное значение «эс» действительно далеко от истинного значения «сигма».

Способ второй. Другой, более простой подход состоит в построении симметричного интервала по формуле:
, где значение  отыскивается по соответствующей таблице.

Согласно таблице, доверительной вероятности  и объёму  соответствует значение , таким образом:

В результате мы получили примерно такой же по размаху интервал. Для малых выборок может даже получиться , в таких случаях принимают ещё более грубую интервальную оценку:

Ответ: 1) , 2) .

Как и для распределения Стьюдента, при увеличении  распределение хи-квадрат стремится к нормальному, и уже при  можно использовать приближенную формулу:
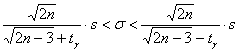, где коэффициент доверия определяется из знакомого лапласовского соотношения .

Иногда встречаются обратная задача – по известной точности оценки (т.е. известному интервалу) найти доверительную вероятность . Иногда требуется построить одностороннюю оценку. Но ввиду их исключительного «иногда», я передаю привет студентам Московского института статистики и продолжаю :)

Точнее завершаю, и ради исследовательского интереса предлагаю продолжить вам – экзаменационный Пример 20:

Пример 26

В результате обработки  экспериментальных данных объёма  мы получили следующие выборочные характеристики: .

В предположении о нормальном распределении генеральной совокупности, с надёжностью  определить доверительные интервалы:

1) для оценки неизвестной генеральной средней ;

2) для оценки генерального среднего квадратического отклонения  двумя способами – с помощью распределения хи-квадрат: 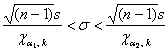 и приближённо, по формул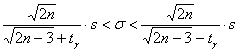е , где .

И заметьте, что здесь «плакал» лёгкий способ построения интервала , так как в стандартной таблице отсутствуют значения для .

Краткое решение и примерный образец оформления в конце урока, который подошёл к концу. В следующей небольшой статье я разберу частную, но весьма популярную задачку по этой же теме – Оценка вероятности биномиального распределения, ну а если вам не терпится, то сразу к послеследующей статье.

До скорых встреч!

Решения и ответы:

Пример 22. Решение:

1) По условию, точность оценки равна  и дисперсия .
Из формулы  найдём коэффициент доверия:

Вычислим соответствующую доверительную вероятность:
 – таким образом, с вероятностью 86,64% можно утверждать, что генеральная средняя  отличается от  менее чем на  (т.е. находится в доверительном интервале от 90 до 96)

2) Для доверительной вероятности :
 – этому значению функции Лапласа соответствует аргумент: .
Вычислим точность оценки:

Определим доверительный интервал:
 
 – данный интервал с вероятностью 99% накрывает истинное значение .

Ответ: а) , б)

Пример 24. Решение: доверительный интервал для оценки истинного значения  измеряемой величины имеет вид:

Для заданного уровня доверительной вероятности  и количества степеней свободы  по таблице распределения Стьюдента находим: .

Вычислим точность оценки:
 сек.

Таким образом, искомый доверительный интервал:

 – данный интервал с вероятностью 99,9% накрывает истинное значение  среднего времени изготовления одного диода.

Ответ:

Пример 26. Решение: вычислим исправленное среднеквадратическое отклонение:

1) Определим  доверительный интервал , где .
Для уровня доверительной вероятности  и объёма выборки  по соответствующей таблице найдём .
Вычислим точность оценки:

Таким образом:

 – с вероятностью  данный интервал накроет генеральное среднее значение .

2) Найдём доверительный интервал для генерального стандартного отклонения .

а) С помощью распределения  :

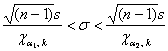
Вычислим  и с помощью соответствующей функции Экселя (Пункт 11б) найдём:

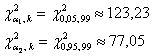
Таким образом:

 – искомый интервал, накрывающий генеральное значение  с вероятностью .

б) Дадим интервальную оценку приближенно, с помощью формулы:

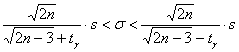
Коэффициент доверия найдём из соотношения . В данном случае:
, и с помощью таблицы или расчётного макета (Пункт 5*), выясняем, что .
Таким образом:

 – искомый интервал.

Ответ:
1) ,
2)  с помощью распределения  и  приближённо.

Автор: Емелин Александр


 Блог Емелина Александра

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?