Однородные дифференциальные уравнения первого порядка

На данном уроке мы рассмотрим так называемые однородные дифференциальные уравнения первого порядка. Наряду с уравнениями с разделяющимися переменными и линейными неоднородными уравнениями этот тип ДУ встречается практически в любой контрольной работе по теме диффуров. Если Вы зашли на страничку с поисковика или не очень уверенно ориентируетесь в дифференциальных уравнениях, то сначала настоятельно рекомендую проработать вводный урок по теме – Дифференциальные уравнения первого порядка. Дело в том, что многие принципы решения однородных уравнений и используемые технические приемы будут точно такими же, как и для уравнений с разделяющимися переменными.

В чём отличие однородных дифференциальных уравнений от других типов ДУ? Это проще всего сразу же пояснить на конкретном примере.

Пример 1

Решить дифференциальное уравнение

Решение: что в первую очередь следует проанализировать при решении любого дифференциального уравнения первого порядка? В первую очередь нужно проверить, а нельзя ли сразу разделить переменные с помощью «школьных» действий? Обычно такой анализ проводят мысленно или пытаются разделить переменные на черновике.

В данном примере переменные разделить нельзя (можете попробовать поперекидывать слагаемые из части в часть, повыносить множители за скобки и т. д.). Кстати, в данном примере, тот факт, что переменные разделить нельзя, достаточно очевиден ввиду наличия множителя .

Возникает вопрос – как же решить этот диффур?

Нужно проверить, а не является ли данное уравнение однородным? Проверка несложная, и сам алгоритм проверки можно сформулировать так:

В исходное уравнение:

вместо подставляем , вместо подставляем , производную не трогаем:

Буква лямбда – это условный параметр, и здесь он играет следующую роль: если в результате преобразований удастся «уничтожить» ВСЕ лямбды и получить исходное уравнение, то данное дифференциальное уравнение является однородным.

Очевидно, что лямбды сразу сокращаются в показателе степени:

Теперь в правой части выносим лямбду за скобки:

и обе части делим на эту самую лямбду:

В результате все лямбды исчезли как сон, как утренний туман, и мы получили исходное уравнение.

Вывод: Данное уравнение является однородным

Поначалу рекомендую проводить рассмотренную проверку на черновике, хотя очень скоро она будет получаться и мысленно.

Как решить однородное дифференциальное уравнение?

У меня очень хорошая новость. Абсолютно все однородные уравнения можно решить с помощью одной-единственной (!) стандартной замены.

Функцию «игрек» следует заменить произведением некоторой функции (тоже зависящей от «икс») и «икса»:

, почти всегда пишут коротко:

Выясняем, во что превратится производная при такой замене, используем правило дифференцирования произведения. Если , то:

Подставляем и в исходное уравнение :

Что даст такая замена? После данной замены и проведенных упрощений мы гарантировано получим уравнение с разделяющимися переменными. ЗАПОМИНАЕМ как первую любовь:) и, соответственно, .

После подстановки проводим максимальные упрощения:

Далее алгоритм работает по накатанной колее уравнения с разделяющимися переменными.

Поскольку – это функция, зависящая от «икс», то её производную можно записать стандартной дробью: .
Таким образом:

Разделяем переменные, при этом в левой части нужно собрать только «тэ», а в правой части – только «иксы»:

Переменные разделены, интегрируем:

Согласно моему первому техническому совету из статьи Дифференциальные уравнения первого порядка, константу во многих случаях целесообразно «оформить» в виде логарифма.

После того, как уравнение проинтегрировано, нужно провести обратную замену, она тоже стандартна и единственна:
Если , то
В данном случае:

В 18-19 случаях из 20 решение однородного уравнения записывают в виде общего интеграла.

Ответ: общий интеграл:

Почему почти всегда ответ однородного уравнения даётся в виде общего интеграла?
В большинстве случаев невозможно выразить «игрек» в явном виде (получить общее решение), а если и возможно, то чаще всего общее решение получается громоздким и корявым.

Так, например, в рассмотренном примере, общее решение получить можно, навешиваем логарифмы на обе части общего интеграла:

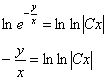
– ну, еще куда ни шло. Хотя, согласитесь, все равно кривовато.

Кстати, в данном примере я не совсем «прилично» записал общий интеграл. Это не ошибка, но в «хорошем» стиле, напоминаю, общий интеграл принято записывать в виде . Для этого сразу после интегрирования уравнения, константу следует записать без всякого логарифма (вот и исключение из правила!):

И после обратной замены получить общий интеграл в «классическом» виде:

Полученный ответ можно проверить. Для этого его нужно продифференцировать, то есть найти производную от функции, заданной неявно:

Избавляемся от дробей, умножая каждую часть уравнения на :

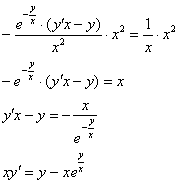
Получено исходное дифференциальное уравнение, значит, решение найдено правильно.

Желательно всегда проводить проверку. Но однородные уравнения неприятны тем, что проверять их общие интегралы обычно трудно – для этого необходима весьма и весьма приличная техника дифференцирования. В рассмотренном примере в ходе проверки уже пришлось находить не самые простые производные (хотя сам по себе пример достаточно простой). Если сможете проверить – проверяйте!

Следующий пример для самостоятельного решения – чтобы вы освоились в самом алгоритме действий:

Пример 2

Проверить уравнение на однородность и найти его общий интеграл.

Ответ записать в виде , выполнить проверку.

...Тут тоже получилась довольно простенькая проверка.

А теперь обещанный важный момент, упомянутый ещё в самом начале темы,
выделю жирными чёрными буквами:

Если в ходе преобразований мы «сбрасываем» множитель с переменной в знаменатель, то РИСКУЕМ потерять решения!

И на самом деле с этим мы столкнулись в первом же примере вводного урока о дифференциальных уравнениях. В процессе решения уравнения «игрек» оказался в знаменателе: , но , очевидно, является решением ДУ и в результате неравносильного преобразования (деления) есть все шансы его потерять! Другое дело, что оно вошло в общее решение при нулевом значении константы. Сброс «икса» в знаменатель тоже можно не принимать во внимание, т. к. не удовлетворяет исходному диффуру.

Аналогичная история с третьим уравнением того же урока, в ходе решения которого мы «сбросили» в знаменатель. Строго говоря, здесь следовало проверить, а не является ли решением данного диффура? Ведь является! Но и тут «всё обошлось», поскольку эта функция вошла в общий интеграл при .

И если с «разделяющимися» уравнениями такое часто ;) «прокатывает», то с однородными и некоторыми другими диффурами может и «не прокатить». С высокой вероятностью.

Проанализируем уже прорешанные задачи этого урока: в Примерах 1-2 «сброс» икса тоже оказался безопасен, ибо там есть и , а посему сразу понятно, что не может быть решением. Кроме того, в Примере 2 в знаменателе оказался , и здесь мы рисковали потерять функцию , которая, очевидно, удовлетворяет уравнению . Однако, и тут «пронесло», т. к. она вошла в общий интеграл при нулевом значении константы.

Но «счастливые случаи» я, конечно же, устроил специально, и не факт, что на практике попадутся именно они:

Пример 3

Решить дифференциальное уравнение

Не правда ли простой пример? ;-)

Решение: однородность этого уравнения очевидна, но всё равно – на первом шаге ОБЯЗАТЕЛЬНО проверяем, нельзя ли разделить переменные. Ибо уравнение тоже однородно, но переменные в нём преспокойно разделяются. Да, бывают и такие!

После проверки на «разделяемость» проводим замену и максимально упрощаем уравнение:

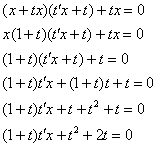
Разделяем переменные, слева собираем «тэ», справа – «иксы»:

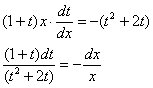
И вот здесь СТОП. При делении на мы рискуем потерять сразу две функции. Так как , то это функции:

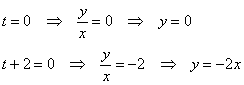
Первая функция, очевидно, является решением уравнения . Проверяем вторую – подставляем и её производную в наш диффур:

– получено верное равенство, значит, функция тоже является решением.

И эти решения мы рискуем потерять.

Кроме того, в знаменателе оказался «икс», и поэтому обязательно проверяем, не является ли решением исходного дифференциального уравнения. Нет, не является. И тут один их читателей задал вопрос: «Почему? Ведь получается уравнение , которое имеет корни». А дело в том, что это не тождество (равенство справедливое для всех функций («игреков»)). Здесь предполагалось , однако не судьба.

Берём всё это на заметку и продолжаем:

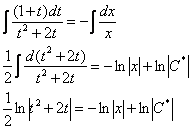
Надо сказать, с интегралом левой части повезло, бывает гораздо хуже.

Перед обратной заменой максимально упрощаем общий интеграл. Если есть дроби, то от них лучше избавиться, умножаем каждую часть на 2:

Константу я переобозначу через :

(если этот момент не понятен, читайте статью Дифференциальные уравнения первого порядка)

Собираем в правой части единый логарифм, и сбрасываем оковы:

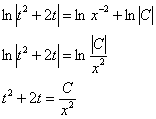
И вот только теперь обратная замена :

Умножим все слагаемые на :

Теперь следует проверить – вошли ли в общий интеграл «опасные» решения . Да, оба решения вошли в общий интеграл при нулевом значении константы: , поэтому их не нужно дополнительно указывать в ответе:

общий интеграл:

Проверка. Даже не проверка, а сплошное удовольствие:)

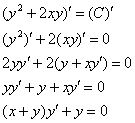
Получено исходное дифференциальное уравнение, значит, решение найдено верно.

Для самостоятельного решения:

Пример 4

Выполнить проверку на однородность и решить дифференциальное уравнение

Общий интеграл проверить дифференцированием.

Полное решение и ответ в конце урока.

Рассмотрим ещё пару типовых примеров:

Пример 5

Решить дифференциальное уравнение

Решение будем привыкать оформлять компактнее. Сначала мысленно либо на черновике убеждаемся в том, что переменные тут разделить нельзя, после чего проводим проверку на однородность – на чистовике её обычно не проводят (если специально не требуется). Таким образом, почти всегда решение начинается с записи: «Данное уравнение является однородным, проведем замену: …».

...замену , и идём проторенной дорогой:

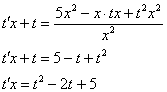
С «иксом» тут всё в порядке, но вот что с квадратным трёхчленом? Поскольку он неразложим на множители: , то решений мы точно не теряем. Всегда бы так! Выделяем в левой части полный квадрат и интегрируем:

Упрощать тут нечего, а посему обратная замена :

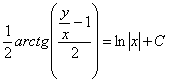
Ответ: общий интеграл:

Следующий пример для самостоятельного решения:

Пример 6

Решить дифференциальное уравнение

...Казалось бы похожие уравнения, ан нет – Большая разница ;)

И сейчас начинается самое интересное! Сначала разберёмся, как быть, если однородное уравнение задано с готовыми дифференциалами:

Пример 7

Решить дифференциальное уравнение

Это очень интересный пример, прямо целый триллер!

Решение: если однородное уравнение содержит готовые дифференциалы, то его можно решить модифицированной заменой:

Но я не советую использовать такую подстановку, поскольку получится Великая китайская стена дифференциалов, где нужен глаз да глаз. С технической точки зрения выгоднее перейти к «штриховому» обозначению производной, для этого делим обе части уравнения на :

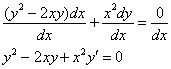
И уже здесь мы совершили «опасное» преобразование! Нулевому дифференциалу соответствует – семейство прямых, параллельных оси . Являются ли они корнями нашего ДУ? Подставим и в исходное уравнение:

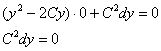
Данное равенство справедливо, если , то есть при делении на мы рисковали потерять решение , и мы его потеряли – так как оно уже не удовлетворяет полученному уравнению .

Следует заметить, что если бы нам изначально было дано уравнение , то о корне речи бы не шло. Но у нас он есть, и мы его вовремя «отловили».

Продолжаем решение стандартной заменой :
:

После подстановки максимально упрощаем уравнение:

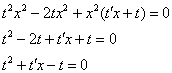
Разделяем переменные:

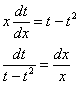
И вот здесь снова СТОП: при делении на мы рискуем потерять две функции. Так как , то это функции:

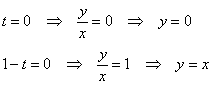
Очевидно, что первая функция является решением уравнения . Проверяем вторую – подставляем и её производную :

– получено верное равенство, значит, функция тоже является решением дифференциального уравнения.

И при делении на мы эти решения рискуем потерять. Впрочем, они могут войти в общий интеграл. Но могут и не войти

Берём это на заметку и интегрируем обе части:

Интеграл левой части стандартно решается с помощью выделения полного квадрата, но в диффурах гораздо удобнее использовать метод неопределенных коэффициентов:

Используя метод неопределенных коэффициентов, разложим подынтегральную функцию в сумму элементарных дробей:

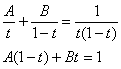
Таким образом:

Находим интегралы:

– так как у нас нарисовались одни логарифмы, то константу тоже заталкиваем под логарифм.

Перед обратной заменой снова упрощаем всё, что можно упростить:

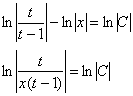
Сбрасываем цепи:

И обратная замена :

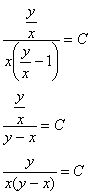
Теперь вспоминаем о «потеряшках»: решение вошло в общий интеграл при , а вот – «пролетело мимо кассы», т. к. оказалось в знаменателе. Поэтому в ответе оно удостаивается отдельной фразы, и да – не забываем о потерянном решении , которое, к слову, тоже оказалось внизу.

Ответ: общий интеграл: . Ещё решения:

Здесь не так трудно выразить общее решение:
, но это уже понты.

Удобные, впрочем, для проверки. Найдём производную:

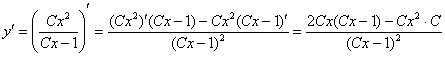
и подставим в левую часть уравнения:

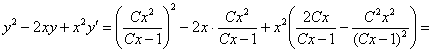
– в результате получена правая часть уравнения, что и требовалось проверить.

Теперь квест с корнями, это тоже распространенный и очень коварный случай:

Пример 8

Решить дифференциальное уравнение

Решение: устно убеждаемся, что уравнение однородно и подставляем первую любовь , в исходное уравнение:

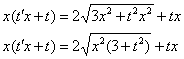
И опасность нас поджидает уже тут. Дело в том, что , и этот факт очень легко упустить из виду:

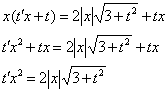
Теперь раскрываем модуль, в результате чего получаются две ветки решения:
, если , и
, если .

Обе ветки удобно записать единым уравнением, при этом возможны следующие варианты оформления:
, где «сигнум икс» – специальная функция, которая возвращает знак «икс»: 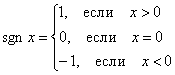, пользуйтесь смело, это известная функция.

Второй способ более привычен, выберу его в качестве рабочего варианта:
, но здесь ОБЯЗАТЕЛЬНО нужен комментарий о том, что знак «+» соответствует случаю , а знак «–» – случаю .

Внимание! Функцию или знаки «отрывать» от корня нельзя! Это может закончиться фатальной ошибкой. Поэтому при разделении переменных знаки мигрируют вместе с корнем в левую часть:
(контролируем, что – не решение)
навешиваем интегралы:

и сейчас вторая новинка, на этот раз по теме «Интегралы». Интеграл , как многие помнят, равен табличному «длинному» логарифму , а интеграл от не только тому же логарифму со знаком «минус», но и его «собрату»: . Желающие могут проверить этот факт дифференцированием.

И в нашем случае общий интеграл удобно записать так:

Упаковываем логарифмы правой части:

…возможно, у некоторых возник вопрос, почему я иногда вдруг убираю модуль под логарифмом? Причина проста – выражение под знаком логарифма, в данном случае , положительно, а значит, модуль записывать не обязательно.

Упрощаем дальше:

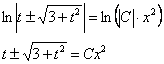
и вот только теперь обратная замена :

Под корнем приведём слагаемые к общему знаменателю:

и небольшое чудо: поскольку , то в результате раскрытия модуля у нас появляются те же два случая со знаками :

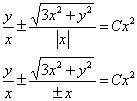
после чего «минусы» сокращаются:

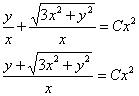
Таким образом, потеря второй ветки решения () нам бы здесь тоже «сошла с рук», но так, разумеется, бывает не всегда, и эту ветку можно реально потерять.

И заключительный штрих, сбрасываем на нижний этаж левой части:

Ответ: общий интеграл:

Я выполнил проверку общего интеграла, но приводить её не буду, а то вы больше не придете к такому маньяку. Да, попробуйте для интереса найти производную. Времяпровождение получите из разряда тех, о которых долго вспоминают. И гордятся.

И в заключение урока своего рода экзаменационный пример:

Пример 9

Решить дифференциальное уравнение

Проконтролируйте, всё ли вы правильно поняли, всё ли учли.

Итак:

при неравносильных преобразованиях ВСЕГДА проверяйте (по крайне мере, устно), не теряете ли вы решения! Какие это преобразования? Как правило, сокращение на что-то, деление на что-то, вынесение из-под корня / внесение под корень. Так, например, при делении на нужно проверить, не являются ли функции решениями дифференциального уравнения. В то же время при делении на надобность такой проверки отпадает – по причине того, что этот делитель не обращается в ноль.

Если проводится замена и есть квадратный корень, то легче лёгкого потерять одну из веток решения, поэтому не забываем про модуль: , и далее сохраняем знаки при корне, несоблюдение этого правила может привести к ошибочному ответу.

Вот ещё одна опасная ситуация:

Здесь, избавляясь от , следует проверить, не является ли решением исходного ДУ. Часто в качестве такого множителя встречается «икс», «игрек», и сокращая на них, мы теряем функции , которые могут оказаться решениями.

С другой стороны, если что-то ИЗНАЧАЛЬНО находится в знаменателе, то повода для такого беспокойства нет. Так, в однородном уравнении можно не беспокоиться о функции , так как она изначально «заявлена» в знаменателе.

Перечисленные тонкости не теряют актуальность, даже если в задаче требуется найти только частное решение. Существует пусть маленький, но шанс, что мы потеряем именно требуемое частное решение. Правда, задача Коши в практических заданиях с однородными уравнениями запрашивается довольно редко (уж не знаю, почему). Тем не менее, такие примеры есть в статье Уравнения сводящиеся к однородным, которую я рекомендую изучить «по горячим следам» чтобы закрепить свои навыки решения.

Существуют и более сложные однородные уравнения. Сложность состоит не в замене переменной или упрощениях, а в достаточно трудных или редких интегралах, которые возникают в результате разделения переменных. У меня есть примеры решений таких однородных уравнений – страшненькие интегралы и страшненькие ответы. Но о них не будем, потому что на ближайших уроках (см. ниже) ~~ещё успею вас замучить~~ я хочу вас видеть свежими и оптимистичными!

Дифференциальные уравнения, сводящиеся к однородным;

Линейные неоднородные дифференциальные уравнения.

Успешного продвижения!

Решения и ответы:

Пример 2. Решение: проверим уравнение на однородность, для этого в исходное уравнение вместо подставим , а вместо подставим :

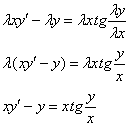
В результате получено исходное уравнение, значит, данное ДУ является однородным.

Проведем замену:
Подставим и в исходное уравнение:

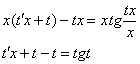
Разделяем переменные и интегрируем:

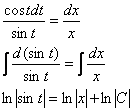
Перед обратной заменой результат целесообразно упростить:

Обратная замена :

Ответ: общий интеграл:

Проверка: дифференцируем ответ:

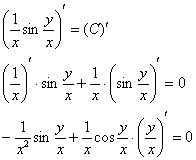
умножаем обе части на :

и делим на :

– получено исходное ДУ, значит, общий интеграл найден верно.

Пример 4. Решение: проверим уравнение на однородность:

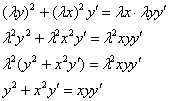
Таким образом, данное уравнение является однородным.
Проведем замену:

После подстановки проводим максимальные упрощения:

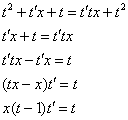
Разделяем переменные и интегрируем:

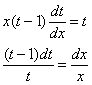
Контроль:
– не является решением уравнения ,
а вот , очевидно, является.
Интегрируем:

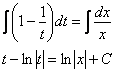
и перед обратной заменой записываем уравнение как можно компактнее:

Проведём обратную замену :

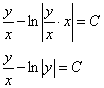
Решение в общий интеграл не вошло, и поэтому его следует дополнительно прописать в ответе:

общий интеграл: . Ещё одно решение:

Проверка:

– в результате получено исходное дифференциальное уравнение, значит, решение найдено верно.

Пример 6. Решение: данное ДУ является однородным, проведем замену :

Разделяем переменные:

Контроль: не является решением, а вот трёхчлен раскладывается на множители: , и поэтому в поле нашего пристального внимания попадают две функции:

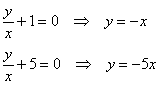
Обе функции являются корнями ДУ (проверьте самостоятельно), и в результате деления мы рискуем потерять эти решения!

Берём их на заметку и продолжаем:

Методом неопределенных коэффициентов получим сумму дробей:

Таким образом:

Получившийся общий интеграл упрощаем:

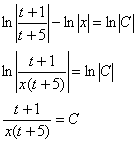
И после упрощений выполняем обратную замену :

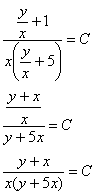
На последнем рубеже вспоминаем о «потеряшках»: функция вошла в общий интеграл (при ), однако – НЕ вошла, и поэтому её необходимо приписать дополнительно:

Ответ: общий интеграл: . Еще одно решение:

Пример 9. Решение: разделим обе части на :

! является решением исходного уравнения.

Данное уравнение является однородным, проведем замену :

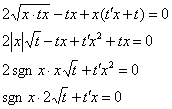
Разделяем переменные, при этом функцию следует обязательно оставить при корне:

(поскольку , если )

Контроль: оказался в знаменателе, а значит, проверке подлежит функция . Подставляем её вместе с её производной в исходное уравнение:
– получено верное равенство, значит, – это одно из решений ДУ.

Интегрируем:

Обратная замена :

Решение не вошло в общий интеграл, и поэтому его следует дополнительно указать в ответе.
Ответ: общий интеграл: , ещё решения: .

Примечание: если по условию требуется найти частное решение, например, с начальным условием , то следует выбрать нужную ветку: (т. к. «икс» равно ) и выполнить подстановку: – искомый частный интеграл.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?