


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Дифференциальные уравнения первого порядка. Примеры решений.
Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения (ДУ). Эти два слова обычно приводят в ужас среднестатистического обывателя. Дифференциальные уравнения кажутся чем-то запредельным и трудным в освоении и многим студентам. Уууууу… дифференциальные уравнения, как бы мне всё это пережить?!
Такое мнение и такой настрой в корне неверен, потому что на самом деле ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ – ЭТО ПРОСТО И ДАЖЕ УВЛЕКАТЕЛЬНО. Что нужно знать и уметь, для того чтобы научиться решать дифференциальные уравнения? Для успешного изучения диффуров вы должны хорошо уметь интегрировать и дифференцировать. Чем качественнее изучены темы Производная функции одной переменной и Неопределенный интеграл, тем будет легче разобраться в дифференциальных уравнениях. Скажу больше, если у вас более или менее приличные навыки интегрирования, то тема практически освоена! Чем больше интегралов различных типов вы умеете решать – тем лучше. Почему? Придётся много интегрировать. И дифференцировать. Также настоятельно рекомендую научиться находить производную от функции, заданной неявно.
Итак, начинаем курс дифференциальных уравнений для начинающих.
В 95% случаев в контрольных работах встречаются 3 типа дифференциальных уравнений первого порядка: уравнения с разделяющимися переменными, которые мы рассмотрим на этом уроке; однородные уравнения и линейные неоднородные уравнения. Начинающим изучать диффуры советую ознакомиться с уроками именно в такой последовательности, причём после изучения первых двух статей не помешает закрепить свои навыки на дополнительном практикуме – уравнения, сводящихся к однородным.
Есть еще более редкие типы дифференциальных уравнений: уравнения в полных дифференциалах, уравнения Бернулли и некоторые другие. Наиболее важными из двух последних видов являются уравнения в полных дифференциалах, поскольку помимо данного ДУ я рассматриваю новый материал – частное интегрирование.
Если у вас в запасе всего день-два, то для сверхбыстрой подготовки есть блиц-курс в pdf-формате. Для чайников и не только.
Ориентиры расставлены – поехали:
сначала вспомним «обычные» уравнения. Они содержат переменные и числа. Детский пример: ![]() . Что значит решить подобное уравнение? Это значит, найти множество всех чисел, которые удовлетворяют данному уравнению. Легко видеть, что наше уравнение имеет единственный корень
. Что значит решить подобное уравнение? Это значит, найти множество всех чисел, которые удовлетворяют данному уравнению. Легко видеть, что наше уравнение имеет единственный корень ![]() . Выполним проверку, подставив четвёрку в уравнение:
. Выполним проверку, подставив четвёрку в уравнение:
![]()
![]() – получено верное равенство, значит, решение найдено правильно.
– получено верное равенство, значит, решение найдено правильно.
Диффуры устроены примерно так же!
Дифференциальное уравнение первого порядка в общем случае содержит:
1) независимую переменную ![]() ;
;
2) зависимую переменную ![]() (функцию);
(функцию);
3) первую производную функции: ![]() .
.
В некоторых уравнениях 1-го порядка может отсутствовать «икс» или (и) «игрек», но это не существенно – важно чтобы в ДУ была первая производная ![]() , и не было производных высших порядков –
, и не было производных высших порядков – ![]() ,
, ![]() и т. д.
и т. д.
Что значит решить дифференциальное уравнение? Решить дифференциальное уравнение – это значит, найти множество всех функций, которые удовлетворяют данному уравнению (впрочем, порой, достаточно одной). То есть корнями дифференциального уравнения являются функции. Для ДУ 1-го порядка такое множество функций зачастую имеет вид ![]() , который называют общим решением дифференциального уравнения («цэ» принимает различные действительные значения).
, который называют общим решением дифференциального уравнения («цэ» принимает различные действительные значения).
Пример 1
Решить дифференциальное уравнение ![]()
Полный боекомплект. С чего начать решение?
В первую очередь нужно переписать производную немного в другом виде. Вспоминаем громоздкое обозначение ![]() , которое многим из вас наверняка казалось нелепым и ненужным. В диффурах рулит именно оно!
, которое многим из вас наверняка казалось нелепым и ненужным. В диффурах рулит именно оно!
Итак:
![]()
На втором шаге смотрим, нельзя ли разделить переменные? Что значит разделить переменные? Грубо говоря, в левой части нам нужно оставить только «игреки», а в правой части организовать только «иксы». Разделение переменных выполняется с помощью «школьных» манипуляций: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т. п.
Дифференциалы ![]() и
и ![]() – это полноправные множители и активные участники боевых действий. В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:
– это полноправные множители и активные участники боевых действий. В рассматриваемом примере переменные легко разделяются перекидыванием множителей по правилу пропорции:
![]()
Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».
Следующий этап – интегрирование дифференциального уравнения. Всё просто, навешиваем интегралы на обе части:
![]()
Разумеется, интегралы нужно взять. В данном случае они табличные:
![]()
Как мы помним, к любой первообразной приписывается константа. Здесь два интеграла, но константу ![]() достаточно записать один раз (т. к. константа + константа всё равно равна другой константе). В большинстве случаев её помещают в правую часть.
достаточно записать один раз (т. к. константа + константа всё равно равна другой константе). В большинстве случаев её помещают в правую часть.
Строго говоря, после того, как взяты интегралы, дифференциальное уравнение считается решённым. Единственное, у нас «игрек» не выражен через «икс», то есть решение представлено в неявном виде. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. То есть ![]() – это общий интеграл.
– это общий интеграл.
Ответ в такой форме вполне приемлем, но нет ли варианта получше? Давайте попытаемся получить общее решение.
Пожалуйста, запомните первый технический приём, он очень распространен и часто применяется в практических заданиях: если в правой части после интегрирования появляется логарифм, то константу во многих случаях (но далеко не всегда!) целесообразно записать тоже под логарифмом. И записать НЕПРЕМЕННО, если получились одни логарифмы (как в рассматриваемом примере).
То есть ВМЕСТО записи ![]() обычно пишут
обычно пишут ![]() (и это корректно, так как
(и это корректно, так как ![]() с таким же успехом принимает все действительные значения, что и
с таким же успехом принимает все действительные значения, что и ![]() ).
).
Зачем это нужно? А для того, чтобы легче было выразить «игрек». Используем свойство логарифмов ![]() . В данном случае:
. В данном случае:
![]()
Теперь логарифмы и модули можно убрать:
![]()
Функция представлена в явном виде. Это и есть общее решение.
Ответ: общее решение: ![]() .
.
Ответы многих дифференциальных уравнений довольно легко проверить. В нашем случае это делается совсем просто, берём найденное решение ![]() и дифференцируем его:
и дифференцируем его:
![]()
После чего подставляем ![]() и производную
и производную ![]() в исходное уравнение
в исходное уравнение ![]() :
:
![]()
![]() – получено равенство, верное для всех значений «икс» (тождество), значит, множество функций
– получено равенство, верное для всех значений «икс» (тождество), значит, множество функций ![]() удовлетворяет уравнению
удовлетворяет уравнению ![]() , что и требовалось проверить.
, что и требовалось проверить.
Придавая константе ![]() различные значения, можно получить бесконечно много частных решений дифференциального уравнения. Ясно, что любая из функций
различные значения, можно получить бесконечно много частных решений дифференциального уравнения. Ясно, что любая из функций ![]() ,
, ![]() ,
, ![]() и т. д. удовлетворяет дифференциальному уравнению
и т. д. удовлетворяет дифференциальному уравнению ![]() .
.
Иногда общее решение называют семейством функций. В данном примере общее решение ![]() – это семейство линейных функций, а точнее, семейство прямых пропорциональностей.
– это семейство линейных функций, а точнее, семейство прямых пропорциональностей.
После обстоятельного разжевывания первого примера уместно ответить на несколько наивных вопросов о дифференциальных уравнениях:
1) В этом примере нам удалось разделить переменные. Всегда ли это можно сделать? Нет, не всегда. И даже чаще переменные разделить нельзя. Например, в однородных уравнениях первого порядка, сначала нужно провести замену. В других типах уравнений, например, в линейном неоднородном уравнении первого порядка, нужно использовать различные приёмы и методы для нахождения общего решения. Уравнения с разделяющимися переменными, которые мы рассматриваем на первом уроке – простейший тип дифференциальных уравнений.
2) Всегда ли можно проинтегрировать дифференциальное уравнение? Нет, не всегда. Очень легко придумать «навороченное» уравнение, которое не проинтегрировать, кроме того, существуют неберущиеся интегралы. Но подобные ДУ можно решить приближенно с помощью специальных методов. Даламбер и Коши гарантируют... …тьфу, Луркмора давеча начитался, чуть не добавил «с того света».
3) В данном примере мы получили решение в виде общего интеграла ![]() . Всегда ли можно из общего интеграла найти общее решение, то есть выразить «игрек» в явном виде? Нет не всегда. Например:
. Всегда ли можно из общего интеграла найти общее решение, то есть выразить «игрек» в явном виде? Нет не всегда. Например: ![]() . Ну и как тут выразить «игрек»?! В таких случаях ответ следует записать в виде общего интеграла. Кроме того, иногда общее решение найти можно, но оно записывается настолько громоздко и коряво, что уж лучше оставить ответ в виде общего интеграла
. Ну и как тут выразить «игрек»?! В таких случаях ответ следует записать в виде общего интеграла. Кроме того, иногда общее решение найти можно, но оно записывается настолько громоздко и коряво, что уж лучше оставить ответ в виде общего интеграла
4) ...Пожалуй, пока достаточно. В первом же примере нам встретился ещё один важный момент, связанный с переносом переменных в знаменатель, но дабы не накрыть «чайников» лавиной информации, оставлю его до следующего урока.
Торопиться не будем. Еще одно простое ДУ и еще один типовой приём решения:
Пример 2
Найти частное решение дифференциального уравнения ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]()
Решение: по условию требуется найти частное решение ДУ, удовлетворяющее заданному начальному условию. Такая постановка вопроса называется задачей Коши.
Сначала находим общее решение. В уравнении нет переменной «икс», но это не должно смущать, главное, в нём есть первая производная.
Переписываем производную в нужном виде:
![]()
Очевидно, что переменные можно разделить, мальчики – налево, девочки – направо:
![]()
Интегрируем уравнение:
![]()
![]()
Общий интеграл получен. Здесь константу я нарисовал с надстрочной звездочкой, дело в том, что очень скоро она превратится в другую константу.
Теперь пробуем общий интеграл преобразовать в общее решение (выразить «игрек» в явном виде). Вспоминаем старое, доброе, школьное: ![]() . В данном случае:
. В данном случае:
![]()
Константа в показателе смотрится как-то некошерно, поэтому её обычно спускают с небес на землю. Если подробно, то происходит это так. Используя свойство степеней, перепишем функцию следующим образом:
![]()
Если ![]() – константа, то
– константа, то ![]() – тоже некоторая константа, переообозначим её через
– тоже некоторая константа, переообозначим её через ![]() :
:
![]()
После чего раскрываем модуль:
![]() и снова переобозначаем константу
и снова переобозначаем константу ![]() , подразумевая, что «цэ» может принимать как положительные, так и отрицательные значения:
, подразумевая, что «цэ» может принимать как положительные, так и отрицательные значения:
![]()
Запомните «снос» константы – это второй технический приём, который часто используют в ходе решения дифференциальных уравнений. На чистовике обычно сразу переходят от ![]() к
к ![]() , но всегда будьте готовы объяснить этот переход. Точно так же как вы – попросили меня объяснить, и я объяснил :)
, но всегда будьте готовы объяснить этот переход. Точно так же как вы – попросили меня объяснить, и я объяснил :)
Итак, общее решение: ![]() . Такое вот симпатичное семейство экспоненциальных функций.
. Такое вот симпатичное семейство экспоненциальных функций.
На завершающем этапе нужно найти частное решение, удовлетворяющее заданному начальному условию ![]() . Это тоже просто.
. Это тоже просто.
В чём состоит задача? Необходимо подобрать такое значение константы ![]() , чтобы выполнялось условие
, чтобы выполнялось условие ![]() .
.
Оформить можно по-разному, но понятнее всего, пожалуй, будет так. В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку:
![]()
![]()
![]()
таким образом, ![]() .
.
Стандартная версия оформления:
![]()
Теперь в общее решение ![]() подставляем найденное значение константы
подставляем найденное значение константы ![]() :
:
![]() – это и есть нужное нам частное решение.
– это и есть нужное нам частное решение.
Ответ: частное решение: ![]()
Выполним проверку. Проверка частного решения включает в себя два этапа:
Сначала нужно проверить, а действительно ли найденная функция ![]() удовлетворяет начальному условию
удовлетворяет начальному условию ![]() ? Вместо «икса» подставляем ноль и смотрим, что получится:
? Вместо «икса» подставляем ноль и смотрим, что получится:
![]() – да, действительно получена двойка, значит, начальное условие выполняется.
– да, действительно получена двойка, значит, начальное условие выполняется.
Второй этап уже знаком. Берём полученную функцию ![]() и находим производную:
и находим производную:
![]()
Подставляем ![]() и
и ![]() в исходное уравнение
в исходное уравнение ![]() :
:
![]()
![]() – получено тождество, далее я буду называть его верным равенством.
– получено тождество, далее я буду называть его верным равенством.
Вывод: частное решение найдено правильно.
Переходим к более содержательным примерам.
Пример 3
Решить дифференциальное уравнение ![]()
Решение: переписываем производную в нужном нам виде:
![]()
Оцениваем, можно ли разделить переменные? Можно. Переносим второе слагаемое в правую часть со сменой знака:
![]()
И перекидываем множители по правилу пропорции:
![]()
Переменные разделены, интегрируем обе части:
![]()
Должен предупредить, приближается судный день. Если вы плохо изучили неопределенные интегралы, прорешали мало примеров, то деваться некуда – придется их осваивать сейчас.
Интеграл левой части легко найти методом подведения функции под знак дифференциала, с интегралом от котангенса расправляемся стандартным приемом, который мы рассматривали на уроке Интегрирование тригонометрических функций в прошлом году:
![]()
![]()
![]()
В результате у нас получились одни логарифмы, и, согласно моей первой технической рекомендации, константу тоже определяем под логарифм.
Теперь пробуем упростить общий интеграл. Поскольку у нас одни логарифмы, то от них можно (и нужно) избавиться. Сначала обе части уравнения удобно умножить на два:
![]()
и переобозначить константу равноценной варьируемой константой ![]() , которая с тем же успехом принимает все действительные значения:
, которая с тем же успехом принимает все действительные значения:
![]()
С помощью известных свойств «упаковываем» логарифмы:
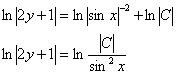
Упаковка завершена, чтобы быть варварски ободранной:
![]() , после чего приводим результат к виду
, после чего приводим результат к виду ![]() , коль скоро это возможно. Так делать, вообще говоря, не обязательно, но всегда же выгодно порадовать профессора ;-)
, коль скоро это возможно. Так делать, вообще говоря, не обязательно, но всегда же выгодно порадовать профессора ;-)
Ответ: общий интеграл: ![]()
! Примечание: общий интеграл часто можно записать не единственным способом. Таким образом, если ваш результат не совпал с заранее известным ответом, то это еще не значит, что вы неправильно решили уравнение.
Можно ли выразить «игрек»? Можно. Давайте выразим общее решение:
![]()
Само собой, полученный результат годится для ответа, но обратите внимание, что общий интеграл смотрится компактнее, да и решение получилось короче.
Третий технический совет: если для получения общего решения нужно выполнить значительное количество действий, то в большинстве случаев лучше воздержаться от этих действий и оставить ответ в виде общего интеграла. Это же касается и «плохих» действий, когда требуется выразить обратную функцию, возвести в степень, извлечь корень и т. п. Дело в том, что общее решение будет смотреться вычурно и громоздко – с большими корнями, знаками ![]() и прочим математическим трэшем.
и прочим математическим трэшем.
Как выполнить проверку? Проверку можно выполнить двумя способами. Способ первый: берём общее решение ![]() , находим производную
, находим производную 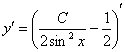 и подставляем их в исходное уравнение
и подставляем их в исходное уравнение ![]() . Попробуйте самостоятельно!
. Попробуйте самостоятельно!
Второй способ состоит в дифференцировании общего интеграла. Это довольно легко, главное, уметь находить производную от функции, заданной неявно:
![]()
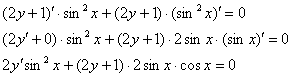
делим каждое слагаемое на ![]() :
:
![]()
и на ![]() :
:
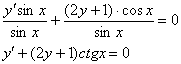
Получено в точности исходное дифференциальное уравнение, значит, общий интеграл найден правильно.
Пример 4
Найти частное решение дифференциального уравнения ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() . Выполнить проверку.
. Выполнить проверку.
Это пример для самостоятельного решения.
Напоминаю, что алгоритм состоит из двух этапов:
1) нахождение общего решения;
2) нахождение требуемого частного решения.
Проверка тоже проводится в два шага (см. образец в Примере № 2), нужно:
1) убедиться, что найденная функцию удовлетворяет начальному условию;
2) проверить, что они вообще удовлетворяет дифференциальному уравнению.
Полное решение и ответ в конце урока.
Пример 5
Найти частное решение дифференциального уравнения ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() . Выполнить проверку.
. Выполнить проверку.
Решение: сначала найдем общее решение. Данное уравнение уже содержит готовые дифференциалы ![]() и
и ![]() , а значит, решение упрощается. Разделяем переменные:
, а значит, решение упрощается. Разделяем переменные:

Интегрируем уравнение:
![]()
Интеграл слева – табличный, интеграл справа – берем методом подведения функции под знак дифференциала:
![]()
![]()
Общий интеграл получен, нельзя ли удачно выразить общее решение? Можно. Навешиваем логарифмы на обе части. Поскольку они положительны, то знаки модуля излишни:
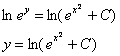
(Надеюсь, всем понятно преобразование ![]() , такие вещи надо бы уже знать)
, такие вещи надо бы уже знать)
Итак, общее решение:
![]()
Найдем частное решение, соответствующее заданному начальному условию ![]() .
.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
![]()
Более привычное оформление: ![]()
Подставляем найденное значение константы ![]() в общее решение.
в общее решение.
Ответ: частное решение: ![]()
Проверка: Сначала проверим, выполнено ли начальное условие ![]() :
:
![]() – всё гуд.
– всё гуд.
Теперь проверим, а удовлетворяет ли вообще найденная функция ![]() дифференциальному уравнению. Находим производную:
дифференциальному уравнению. Находим производную:
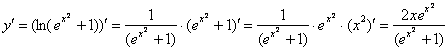
Смотрим на исходное уравнение: ![]() – оно представлено в дифференциалах. Есть два способа проверки. Можно из найденной производной выразить дифференциал
– оно представлено в дифференциалах. Есть два способа проверки. Можно из найденной производной выразить дифференциал ![]() :
:
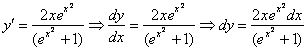
Подставим функцию ![]() и полученный дифференциал
и полученный дифференциал  в исходное уравнение
в исходное уравнение ![]() :
:

Используем основное логарифмическое тождество ![]() :
:

Получено верное равенство, таким образом, частное решение найдено правильно.
Второй способ проверки зеркален и более привычен: из уравнения ![]() выразим производную, для этого разделим все штуки на
выразим производную, для этого разделим все штуки на ![]() :
:

И в полученное ДУ подставим ![]() с найденной производной
с найденной производной  . В результате упрощений тоже должно получиться верное равенство.
. В результате упрощений тоже должно получиться верное равенство.
Пример 6
Найти общий интеграл уравнения ![]() , ответ представить в виде
, ответ представить в виде ![]() .
.
Это пример для самостоятельного решения, полное решение и ответ в конце урока.
Какие трудности подстерегают при решении дифференциальных уравнений с разделяющимися переменными?
1) Не всегда очевидно (особенно, «чайнику»), что переменные можно разделить. Рассмотрим условный пример: ![]() . Здесь нужно провести вынесение множителей за скобки:
. Здесь нужно провести вынесение множителей за скобки: ![]() и отделить корни:
и отделить корни: ![]() . Как действовать дальше – понятно.
. Как действовать дальше – понятно.
2) Сложности при самом интегрировании. Интегралы нередко возникают не самые простые, и если есть изъяны в навыках нахождения неопределенного интеграла, то со многими диффурами придется туго. К тому же у составителей сборников и методичек популярна логика «раз уж дифференциальное уравнение является простым, то пусть хоть интегралы будут посложнее».
3) Преобразования с константой. Как все заметили, с константой в дифференциальных уравнениях можно обращаться достаточно вольно, и некоторые преобразования не всегда понятны новичку. Рассмотрим ещё один условный пример: ![]() . В нём целесообразно умножить все слагаемые на 2:
. В нём целесообразно умножить все слагаемые на 2: ![]() . Полученная константа
. Полученная константа ![]() – это тоже какая-то константа, которую можно обозначить через
– это тоже какая-то константа, которую можно обозначить через ![]() :
: ![]() . Да, и поскольку у нас одни логарфимы, то константу
. Да, и поскольку у нас одни логарфимы, то константу ![]() целесообразно переписать в виде другой константы:
целесообразно переписать в виде другой константы: ![]() .
.
Беда же состоит в том, что с индексами часто не заморачиваются и используют одну и ту же букву ![]() . В результате запись решения принимает следующий вид:
. В результате запись решения принимает следующий вид:
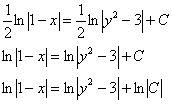
Что за дела?! Тут же ошибки! Строго говоря – да. Однако с содержательной точки зрения, ошибок нет, ведь в результате преобразования варьируемой константы получается равноценная варьируемая константа.
Или другой пример, предположим, что в ходе решения уравнения получен общий интеграл ![]() . Такой ответ выглядит некрасиво, поэтому у каждого слагаемого целесообразно сменить знак:
. Такой ответ выглядит некрасиво, поэтому у каждого слагаемого целесообразно сменить знак: ![]() . Формально здесь опять ошибка – справа следовало бы записать
. Формально здесь опять ошибка – справа следовало бы записать ![]() . Но неформально подразумевается, что «минус цэ» – это всё равно константа, которая с тем же успехом принимает то же множество значений, и поэтому ставить «минус» не имеет смысла.
. Но неформально подразумевается, что «минус цэ» – это всё равно константа, которая с тем же успехом принимает то же множество значений, и поэтому ставить «минус» не имеет смысла.
Я буду стараться избегать небрежного подхода, и всё-таки проставлять у констант разные индексы при их преобразовании. Чего и вам советую делать.
Пример 7
Решить дифференциальное уравнение ![]() . Выполнить проверку.
. Выполнить проверку.
Решение: Данное уравнение допускает разделение переменных. Разделяем переменные:
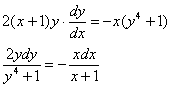
Интегрируем. В левой части подводим функцию под знак дифференциала, а в правой используем стандартный искусственный приём:
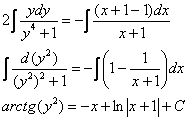
Константу ![]() тут не обязательно определять под логарифм, поскольку ничего путного из этого не получится.
тут не обязательно определять под логарифм, поскольку ничего путного из этого не получится.
Ответ: общий интеграл: ![]()
И, разумеется, здесь НЕ НАДО выражать «игрек» в явном виде, ибо получится трэш (вспоминаем третий технический совет).
Проверка: дифференцируем ответ (неявную функцию):
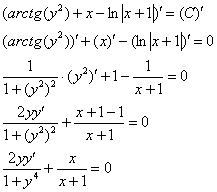
Избавляемся от дробей, для этого умножаем оба слагаемых на ![]() :
:
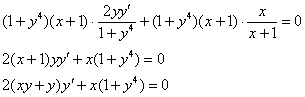
Получено исходное дифференциальное уравнение, значит, общий интеграл найден правильно.
Пример 8
Найти частное решение ДУ.
![]() ,
, ![]()
Это пример для самостоятельного решения. Единственная подсказка – здесь получится общий интеграл, и, правильнее говоря, нужно исхитриться найти не частное решение, а частный интеграл. Полное решение и ответ в конце урока.
Как уже отмечалось, в диффурах с разделяющимися переменными нередко вырисовываются не самые простые интегралы. И вот еще парочка таких примеров для самостоятельного решения. Рекомендую всем прорешать Примеры № 9-10, независимо от уровня подготовки, это позволит актуализировать навыки нахождения интегралов или восполнить пробелы в знаниях.
Пример 9
Решить дифференциальное уравнение ![]()
Пример 10
Решить дифференциальное уравнение ![]()
Помните, что общий интеграл можно записать не единственным способом, и внешний вид ваших ответов может отличаться от внешнего вида моих ответов – яркая тому иллюстрация встретилась в Примере 8, где я добавил второй вариант по причине неоднократных вопросов. Краткие решения и ответы в конце урока.
Следующая рекомендуемая статья – Однородные дифференциальные уравнения первого порядка.
Успешного продвижения!
Решения и ответы:
Пример 4. Решение: найдем общее решение. Разделяем переменные:
![]()
![]()
Интегрируем:
![]()
![]()
![]()
Общий интеграл получен, пытаемся его упростить. Упаковываем логарифмы и избавляемся от них:
![]()
![]()
![]()
Выражаем функции в явном виде, используя ![]() .
.
Общее решение: ![]()
Найдем частное решение, удовлетворяющее начальному условию ![]() .
.
Способ первый, вместо «икса» подставляем 1, вместо «игрека» – «е»:
![]() .
.
Способ второй:
![]()
Подставляем найденное значение константы ![]() в общее решение.
в общее решение.
Ответ: частное решение: ![]()
Проверка: проверяем, действительно ли выполняется начальное условие:
![]() , да, начальное условие
, да, начальное условие ![]() выполнено.
выполнено.
Проверяем, удовлетворяет ли вообще функция ![]() дифференциальному уравнению. Сначала находим производную:
дифференциальному уравнению. Сначала находим производную:
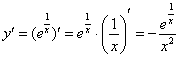
Подставим функцию ![]() и найденную производную
и найденную производную 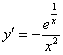 в исходное уравнение
в исходное уравнение ![]() :
:
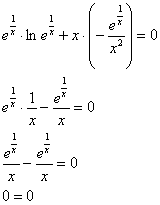
Получено верное равенство, значит, решение найдено правильно.
Пример 6. Решение: данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
![]()
![]()
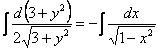
![]()
Ответ: общий интеграл: ![]()
Примечание: тут можно получить и общее решение:
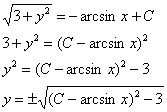
Но, согласно моему третьему техническому совету, делать это нежелательно, поскольку такой ответ смотрится довольно плохо.
Пример 8. Решение, вариант первый: данное ДУ допускает разделение переменных. Разделяем переменные:
![]()
![]()
![]()
Интегрируем:
![]()
![]()
Общий интеграл: ![]()
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию ![]() . Подставляем в общее решение
. Подставляем в общее решение ![]() и
и ![]() :
:
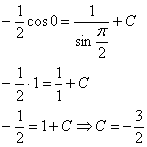
Ответ: частный интеграл: ![]()
В принципе, ответ можно попричесывать и получить что-нибудь более компактное.
Вариант второй: интеграл левой части можно взять по-другому:
![]()
В результате получаем следующий общий интеграл:
![]()
Найдем частный интеграл, соответствующий условию ![]() :
:
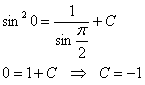
Таким образом:
![]()
Этот результат легко свести к 1-му ответу, применим формулу ![]() :
:
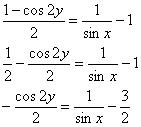
Пример 9. Решение: данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
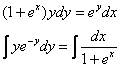
Левую часть интегрируем по частям:
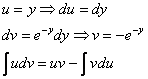
В интеграле правой части проведем замену:
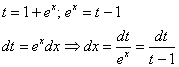
Таким образом:
![]()
![]()
(здесь дробь раскладывается методом неопределенных коэффициентов, но она настолько простая, что подбор коэффициентов можно выполнить и устно)
![]()
Обратная замена: ![]()
![]()
![]()
![]()
Ответ: общий интеграл: ![]()
Пример 10. Решение: данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
![]()
![]()
![]()
![]()
![]()
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
![]()
![]()
Примечание: интеграл ![]() можно было также найти методом выделения полного квадрата.
можно было также найти методом выделения полного квадрата.
![]()
![]()
![]()
![]()
![]()
Ответ: общее решение: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright