


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
9. Оценка вероятности биномиального распределения
Оценка вероятности биномиального распределения – это одна из частных задач по теме статистических оценок, и даже если вы не поняли этих слов, ничего страшного. Ибо на носу очередной Новый год, и на этот раз я не собираюсь вам дарить дифференциальные уравнения:)
– пусть проводятся независимые испытания, в каждом из которых некоторое событие ![]() может наступить с вероятностью
может наступить с вероятностью ![]() , причём эта вероятность нам не известна. Да, на этот раз не известна.
, причём эта вероятность нам не известна. Да, на этот раз не известна.
И в канун праздника мне пришёл в голову такой пример: представьте игровой автомат или некую игру, в котором разыгрываются призы. Игрушки, зверушки и прочие товары для взрослых мандаринки. Разумеется, мы не знаем вероятность ![]() выигрыша в каждой попытке. Но её реально оценить, и оценить весьма точно, чему и посвящён этот небольшой урок.
выигрыша в каждой попытке. Но её реально оценить, и оценить весьма точно, чему и посвящён этот небольшой урок.
Поставленную задачу поможет решить математическая статистика и группа студентов, которая совершила ![]() испытаний (в хорошем смысле слова:)) и выиграла
испытаний (в хорошем смысле слова:)) и выиграла ![]() призов. Тогда относительная частота
призов. Тогда относительная частота ![]() представляет собой точечную оценку неизвестной вероятности
представляет собой точечную оценку неизвестной вероятности ![]() .
.
Теперь предположим, что другая группа студентов тоже совершила серию испытаний (не обязательно 300 раз). Какой будет результат? Почти наверняка они выиграют иную долю призов, то есть, получат другую относительную частоту. И, проводя многократные серии испытаний по всему университету, мы получим множество точечных оценок, которые будут варьироваться вокруг точного значения ![]() .
.
Как отмечалось ранее, недостаток точечной оценки состоит в том, что она может оказаться далека от истины (особенно, при малом ![]() ) и поэтому вероятность
) и поэтому вероятность ![]() выгодно оценить интервалом:
выгодно оценить интервалом:
![]() – который с заранее выбранной доверительной вероятностью
– который с заранее выбранной доверительной вероятностью ![]() накроет истинное значение
накроет истинное значение ![]() .
.
Напоминаю, что ![]() («дельта») называется точностью оценки и вышесказанное можно записать компактнее:
(«дельта») называется точностью оценки и вышесказанное можно записать компактнее:
![]() – вероятность, того, что относительная частота
– вероятность, того, что относительная частота ![]() отклонится от вероятности
отклонится от вероятности ![]() менее чем на
менее чем на ![]() .
.
И давайте оформим демонстрационную задачу формально:
Пример 27
Проводят независимые испытания с одинаковой, но неизвестной вероятностью ![]() появления события
появления события ![]() в каждом испытании. Найти доверительный интервал для оценки вероятности
в каждом испытании. Найти доверительный интервал для оценки вероятности ![]() с надёжностью
с надёжностью ![]() , если в
, если в ![]() испытаниях событие
испытаниях событие ![]() появилось
появилось ![]() раз.
раз.
Да, кстати, если в вашей задаче вероятность ![]() известна, то такие задачи мы разбирали на уроке о статистической вероятности с той поправкой, что вместо буквы
известна, то такие задачи мы разбирали на уроке о статистической вероятности с той поправкой, что вместо буквы ![]() там использовалась
там использовалась ![]() .
.
Решение: если количество испытаний ![]() достаточно велико (порядка сотни и больше) и значение
достаточно велико (порядка сотни и больше) и значение ![]() не слишком малО *, то требуемый доверительный интервал можно построить по следующей приближенной формуле:
не слишком малО *, то требуемый доверительный интервал можно построить по следующей приближенной формуле:
![]() , где
, где ![]() – относительная частота, а
– относительная частота, а ![]() – коэффициент доверия, отыскиваемый из соотношения
– коэффициент доверия, отыскиваемый из соотношения ![]() . Надеюсь, все уже знают функцию
. Надеюсь, все уже знают функцию ![]() . …Но я-то всё равно напомню, даже не надейтесь :)
. …Но я-то всё равно напомню, даже не надейтесь :)
* Примечание: при этих условиях биномиальное распределение близкО к нормальному. Несложный вывод этой и более точной формулы можно найти, например, в учебном пособии В.Е. Гмурмана.
Вычислим относительную частоту ![]() и точность оценки
и точность оценки ![]() . Коэффициент доверия найдём из соотношения
. Коэффициент доверия найдём из соотношения ![]() , в данном случае:
, в данном случае:
![]() , следовательно:
, следовательно:
![]() и по таблице значений функции Лапласа или с помощью расчётного макета (Пункт 5*) определяем, что этому значению функции соответствует аргумент
и по таблице значений функции Лапласа или с помощью расчётного макета (Пункт 5*) определяем, что этому значению функции соответствует аргумент ![]() .
.
Таким образом, точность оценки:
![]() и искомый доверительный интервал:
и искомый доверительный интервал:
![]()
![]() – с вероятностью
– с вероятностью ![]() этот интервал накрывает истинную вероятность выигрыша в нашей новогодней игре.
этот интервал накрывает истинную вероятность выигрыша в нашей новогодней игре.
Ответ: ![]()
Оценка получилась неплохая, но её неплохо бы улучшить, т.е. уменьшить значение ![]() , сузив тем самым интервал. Очевидно, что для этого нужно увеличить количество
, сузив тем самым интервал. Очевидно, что для этого нужно увеличить количество ![]() испытаний, что совершенно логично. Есть вариант уменьшить коэффициент доверия
испытаний, что совершенно логично. Есть вариант уменьшить коэффициент доверия ![]() , но тогда упадёт и доверительная вероятность, поэтому это плохой вариант.
, но тогда упадёт и доверительная вероятность, поэтому это плохой вариант.
Обратная задача для самостоятельного решения. Тоже праздничная, о шариках. В подшипниках:
Пример 28
Из 500 поступивших на сортировку шариков для подшипников 200 попало в первую группу. В предположении о биномиальном распределении, определить:
1) доверительную вероятность того, что найденная доля шариков отклонится от вероятности попадания шарика в первую группу, менее чем на 0,03.
…все поняли эту фразу? :) …нет, я не специально – это реальная задача, поэтому разберитесь в условии!
2) доверительную вероятность того, что вероятность попадания шарика в 1-ю группу будет накрыта интервалом ![]() .
.
Для первой части сразу приведу готовую формулу: 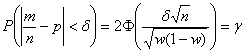 , где аргумент функции Лапласа – не что иное, как коэффициент доверия
, где аргумент функции Лапласа – не что иное, как коэффициент доверия 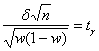 , и расчётный макет (Пункт 5) вам в помощь. А вот вторая часть – творческая, в ней предложен несимметричный относительно
, и расчётный макет (Пункт 5) вам в помощь. А вот вторая часть – творческая, в ней предложен несимметричный относительно ![]() доверительный интервал.
доверительный интервал.
Краткое решение с комментариями в конце урока.
И ещё один сюрприз состоит в том, что эта статья получилась короткой – это подарок для вас, это подарок для меня, и сейчас мы разберём ещё одну важную и интересную вариацию рассматриваемой задачи, которая касается как раз количества испытаний:
Пример 29
Проверив ![]() изделий, обнаружили, что
изделий, обнаружили, что ![]() изделий первого сорта. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю первосортных изделий с точностью до 0,01?
изделий первого сорта. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю первосортных изделий с точностью до 0,01?
Сразу вычислим относительную частоту ![]() и для исследовательского интереса найдём вероятность
и для исследовательского интереса найдём вероятность ![]() , с которой истинное значение
, с которой истинное значение ![]() накрывается столь узким интервалом
накрывается столь узким интервалом ![]() .
.
Примечание: параметр ![]() – есть вероятность того, что наугад извлечённое изделие окажется первосортным, его также называют генеральной долей (изделий высшего сорта) и чаще обозначают буквой
– есть вероятность того, что наугад извлечённое изделие окажется первосортным, его также называют генеральной долей (изделий высшего сорта) и чаще обозначают буквой ![]() .
.
Используем формулу 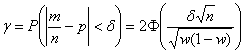 . В данном случае:
. В данном случае:
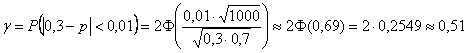 – ну, и, конечно, такое кислое значение никуда не годится – тут уж проще монетку подбросить, чем всё это считать :)
– ну, и, конечно, такое кислое значение никуда не годится – тут уж проще монетку подбросить, чем всё это считать :)
Поэтому в задаче и требуется обеспечить надёжность ![]() , и решение проводится по той же формуле:
, и решение проводится по той же формуле:
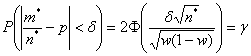 – откуда следует отыскать
– откуда следует отыскать ![]() – объём выборки, обеспечивающий столь высокую доверительную вероятность.
– объём выборки, обеспечивающий столь высокую доверительную вероятность.
В данном случае:
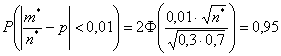 , следовательно:
, следовательно:
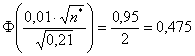 – и по таблице значений функции Лапласа либо по расчётному макету (Пункт 5*) выясняем, что этому значению функции соответствует аргумент 1,96:
– и по таблице значений функции Лапласа либо по расчётному макету (Пункт 5*) выясняем, что этому значению функции соответствует аргумент 1,96:
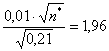
теперь технически удобно возвести обе части в квадрат:
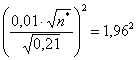
и найти искомый объём выборки:
![]() – тут логично округлить в бОльшую сторону.
– тут логично округлить в бОльшую сторону.
Итак, для того, чтобы с уверенностью 95% определить долю первого сорта с точностью до 0,01, нужно проверить, ответ: 8068 изделий
И если проверять изделия вручную, то это, конечно, многовато. Поэтому в подобном случае лучше поступиться точностью оценки ![]() , и для исследовательского интереса я предлагаю вам те же значения
, и для исследовательского интереса я предлагаю вам те же значения ![]() , для которых нужно построить доверительный интервал, который с вероятностью
, для которых нужно построить доверительный интервал, который с вероятностью ![]() накроет истинную долю
накроет истинную долю ![]() первосортных изделий.
первосортных изделий.
Краткое решение совсем близко, и в оставшуюся до НГ неделю я таки успел порадовать вас ещё одной статьей – об оценках по повторной и бесповторной выборке, где, в частности рассмотрены вариации только что разобранной задачи.
Решения и ответы:
Пример 28. Решение: вычислим относительную частоту ![]() и обозначим через
и обозначим через ![]() неизвестную вероятность того, что шарик попадёт в 1-ю группу.
неизвестную вероятность того, что шарик попадёт в 1-ю группу.
1) Используем формулу 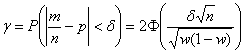 . В данном случае
. В данном случае ![]() , таким образом:
, таким образом:
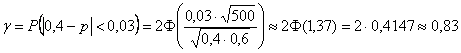 – вероятность того, что, что значение
– вероятность того, что, что значение ![]() будет отличаться от
будет отличаться от ![]() менее чем на
менее чем на ![]() .
.
Иными словами, интервал ![]() с вероятностью
с вероятностью ![]() накрывает истинное значение
накрывает истинное значение ![]() .
.
2) Предложенный доверительный интервал ![]() не симметричен относительно относительной частоты
не симметричен относительно относительной частоты ![]() и имеет вид:
и имеет вид: ![]() , где
, где ![]() .
.
Запишем левостороннюю точность оценки: ![]() и найдём соответствующий коэффициент доверия:
и найдём соответствующий коэффициент доверия:
![]() .
.
По таблице значений функции Лапласа:
![]() – левосторонняя доверительная вероятность.
– левосторонняя доверительная вероятность.
Аналогично для правой стороны:
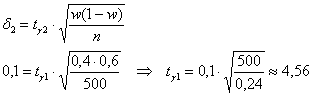
![]() – правосторонняя доверительная вероятность.
– правосторонняя доверительная вероятность.
Таким образом, двусторонняя доверительная вероятность составляет:
![]() – иными словами с такой вероятностью интервал
– иными словами с такой вероятностью интервал ![]() накрывает истинное значение
накрывает истинное значение ![]() .
.
Ответ: а) ![]() , б)
, б) ![]()
К Примеру 29: Решение: построим доверительный интервал:
![]()
Из соотношения ![]() найдём:
найдём:
![]() , откуда следует, что
, откуда следует, что ![]() .
.
Вычислим точность оценки:
![]() – как видите, точность вполне удовлетворительна.
– как видите, точность вполне удовлетворительна.
Таким образом:
![]()
![]() – с вероятностью 95% можно утверждать, что этот интервал накрывает истинное значение генеральной доли
– с вероятностью 95% можно утверждать, что этот интервал накрывает истинное значение генеральной доли ![]() первосортных изделий.
первосортных изделий.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright