


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как найти функцию комплексной переменной
по известной действительной или мнимой части?
Рассмотрим еще одну распространенную задачу комплексного анализа: нахождение функции комплексной переменной по известной действительной или мнимой части. Для её освоения нужно ориентироваться в материалах урока Производная функции комплексной переменной, ну а если вы только приступили к изучению ТФКП – начните с азов темы.
Сначала вернёмся к задаче предыдущего занятия: дана функция комплексной переменной ![]() . Требуется найти действительную
. Требуется найти действительную ![]() и мнимую
и мнимую ![]() части функции и проверить условия Коши-Римана. Найти производную
части функции и проверить условия Коши-Римана. Найти производную ![]() , если это возможно. Опционально производную в точке, фантазия математических злодеев здесь бедновата.
, если это возможно. Опционально производную в точке, фантазия математических злодеев здесь бедновата.
Коротко повторим алгоритм решения данной задачи: на первом этапе следует выполнить подстановку ![]() . Сразу же напоминаю две наиболее ходовые формулы:
. Сразу же напоминаю две наиболее ходовые формулы:
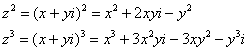
В результате функция комплексной переменной должна быть представлена в виде:
![]()
Далее идёт проверка условий Коши-Римана. Здесь нужно найти четыре частных производных и убедиться в справедливости равенств:
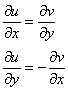
В практических примерах условия Коши-Римана выполняются в большинстве случаев, а значит, можно взять производную ![]() .
.
Зачем я всё это повторил заново? Дело в том, что сейчас нам предстоит рассмотреть обратную задачу, которая формулируется примерно так:
дана действительная ![]() часть аналитической функции
часть аналитической функции ![]() . Требуется найти её мнимую часть
. Требуется найти её мнимую часть ![]() . Найти саму функцию
. Найти саму функцию ![]() , используя заданное начальное условие.
, используя заданное начальное условие.
Алгоритм решения будет раскручиваться в обратном направлении:
1) Используя условия Коши-Римана, находим мнимую часть ![]() . Очень хорошо, если вы разобрались с дифференциальными уравнениями в полных дифференциалах, так как хитросплетения первого этапа будут точно такими же, как в тех диффурах.
. Очень хорошо, если вы разобрались с дифференциальными уравнениями в полных дифференциалах, так как хитросплетения первого этапа будут точно такими же, как в тех диффурах.
2) Теперь и действительная и мнимая части известны, поэтому составляем функцию ![]() . Дальнейшие действия будут направлены на то, чтобы все «иксы» и «игреки» превратить в «зеты». В частности, наиболее распространенные формулы будут работать в обратном направлении:
. Дальнейшие действия будут направлены на то, чтобы все «иксы» и «игреки» превратить в «зеты». В частности, наиболее распространенные формулы будут работать в обратном направлении:
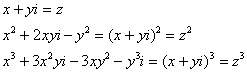
То есть из каши ![]() с помощью раскрытия скобок, перегруппировки слагаемых и т. д. следует выуживать жирные куски масла. Например, составить выражение
с помощью раскрытия скобок, перегруппировки слагаемых и т. д. следует выуживать жирные куски масла. Например, составить выражение ![]() и превратить его в
и превратить его в ![]() .
.
3) На завершающем этапе будет получена функция ![]() , в которой есть только комплексная переменная «зет» и константы. Используя начальное условие, окончательно уточняем функцию
, в которой есть только комплексная переменная «зет» и константы. Используя начальное условие, окончательно уточняем функцию ![]() . Действие несложное, более подробно вернёмся к нему в практических примерах.
. Действие несложное, более подробно вернёмся к нему в практических примерах.
Очевидно, существует и «зеркальная» задача: когда по условию дана мнимая часть ![]() , а требуется найти действительную часть
, а требуется найти действительную часть ![]() . Алгоритм решения практически тот же самый – с помощью условий Коши-Римана находим действительную часть
. Алгоритм решения практически тот же самый – с помощью условий Коши-Римана находим действительную часть ![]() , и понеслась нелёгкая.
, и понеслась нелёгкая.
Обе задачи встречаются одинаково часто, и я постараюсь максимально детально разобрать оба случая.
Пример 1
Дана действительная часть ![]() функции комплексной переменной. Найти мнимую часть
функции комплексной переменной. Найти мнимую часть ![]() данной функции и составить функцию
данной функции и составить функцию ![]() , удовлетворяющую начальному условию
, удовлетворяющую начальному условию ![]() .
.
Решение:
1) Сначала найдем мнимую часть функции ![]() . В распоряжении у нас есть действительная часть. А что с неё взять, кроме частных производных?
. В распоряжении у нас есть действительная часть. А что с неё взять, кроме частных производных?
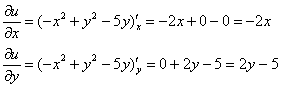
Вспоминаем условия Коши-Римана:
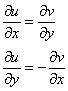
В целях решения данной задачи равенства удобнее переписать в другом порядке:
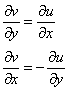
В соответствии с первым условием:
![]()
В соответствии со вторым условием:
![]() – обратите внимание на смену знака.
– обратите внимание на смену знака.
В результате у нас протянулся мостик к неизвестной мнимой части в виде двух её частных производных:
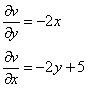
Следующий этап полностью совпадает с решением дифференциального уравнения в полных дифференциалах, то есть по двум частным производным необходимо восстановить общий интеграл ![]() (мнимую часть). Не сильно хочется, но хотя бы один раз вновь всё пропишу подробно:
(мнимую часть). Не сильно хочется, но хотя бы один раз вновь всё пропишу подробно:
![]() – работаем с этой производной;
– работаем с этой производной;
![]() – про эту производную пока забываем.
– про эту производную пока забываем.
Примечание: как вариант, можно «забыть» о первой производной, а пляску начинать со второй – получится совершенно равноценное решение. Этот момент хорошо показан в соответствующей статье (см. ссылку выше).
Поскольку ![]() , то общий интеграл
, то общий интеграл ![]() восстанавливаем частным интегрированием по «игрек»:
восстанавливаем частным интегрированием по «игрек»:
![]() , где
, где ![]() – неизвестная функция, зависящая только от «икс».
– неизвестная функция, зависящая только от «икс».
Напоминаю, что при частном интегрировании по «игрек» – «икс» считается константой, поэтому ![]() можно вынести за знак интеграла. Для самопроверки всегда полезно найти частную производную:
можно вынести за знак интеграла. Для самопроверки всегда полезно найти частную производную: ![]() (функция
(функция ![]() зависит только от «икс», поэтому её производная по «игрек» равна нулю).
зависит только от «икс», поэтому её производная по «игрек» равна нулю).
Теперь от нашей недоделанной мнимой части ![]() берём частную производную по «икс»:
берём частную производную по «икс»:
![]() – и результат приравниваем к «забытой» частной производной:
– и результат приравниваем к «забытой» частной производной:
![]()
После сокращений получаем:
![]()
Восстанавливаем функцию ![]() интегрированием:
интегрированием:
![]()
Подставляем найденную функцию ![]() в недоделанную мнимую часть
в недоделанную мнимую часть ![]() . В итоге, после всех манипуляций:
. В итоге, после всех манипуляций:
![]() – мнимая часть функции
– мнимая часть функции ![]()
2) Действие второе. Найдем функцию ![]() :
:
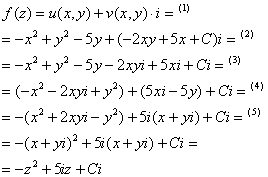
(1) Подставляем действительную часть ![]() , которая была дана в условии и найденную мнимую часть
, которая была дана в условии и найденную мнимую часть ![]() .
.
(2) Раскрываем скобки.
(3) Выполняем перегруппировку слагаемых, для удобства я заключил их в скобки. В целях перегруппировки нужно проанализировать, что в ближайшей перспективе может получиться? Так, например, смотрим на слагаемое ![]() , и в голову приходит мысль, что тут будет фигурировать формула
, и в голову приходит мысль, что тут будет фигурировать формула ![]() , поэтому и собираем вместе слагаемые, которые очевидно будут относиться к данной формуле.
, поэтому и собираем вместе слагаемые, которые очевидно будут относиться к данной формуле.
(4) Проводим вынесение за скобки некоторых множителей, учитывая, что в нашей функции ![]() всё дело явно сведётся к двум формулам:
всё дело явно сведётся к двум формулам: ![]() .
.
При этом всегда можно сделать проверку, раскрыв скобки, например:
![]() .
.
(5) Используя две вышеуказанные формулы, получаем функцию ![]()
Обратите внимание, что в функции ![]() присутствует только комплексная переменная «зет» и константы. Если остался какой-нибудь мусор с «иксами», «игреками», значит, вы допустили ошибку где-то выше.
присутствует только комплексная переменная «зет» и константы. Если остался какой-нибудь мусор с «иксами», «игреками», значит, вы допустили ошибку где-то выше.
3) Третий этап короткий. Найдём значение константы ![]() . В соответствии с начальным условием
. В соответствии с начальным условием ![]() :
:
![]()
Согласно условию, в ответ следует записать мнимую часть и саму функцию, естественно, с учётом найденного значения константы ![]() :
:
![]() ,
, ![]()
Да, конечно, задача не из самых простых, но с другой стороны, весьма логично – конструировать гораздо труднее, чем разрушать. И коль скоро разрушать проще, то проверка элементарна. Сначала проверяем выполнение начального условия ![]() :
:
![]() – начальное условие выполнено.
– начальное условие выполнено.
Второй этап проверки – представить найденную функцию ![]() в виде
в виде ![]() , иными словами, в точности решить задачу, которая подробно разобрана на уроке Производная функции комплексной переменной.
, иными словами, в точности решить задачу, которая подробно разобрана на уроке Производная функции комплексной переменной.
Творческий пример для самостоятельного решения:
Пример 2
Дана действительная часть ![]() функции комплексной переменной. Найти мнимую часть
функции комплексной переменной. Найти мнимую часть ![]() данной функции и составить функцию
данной функции и составить функцию ![]() , удовлетворяющую начальному условию
, удовлетворяющую начальному условию ![]() .
.
Примерный образец чистового оформления и ответ в конце урока.
И тут у вас наверняка появился вопрос: вот нам дана произвольная функция ![]() – всегда ли существует функция
– всегда ли существует функция ![]() , такая, чтобы выполнялись условия Коши-Римана? Конечно, нет. Ведь есть туча недифференцируемых функций, для которых условия Коши-Римана не выполнены, зачастую на всей комплексной плоскости.
, такая, чтобы выполнялись условия Коши-Римана? Конечно, нет. Ведь есть туча недифференцируемых функций, для которых условия Коши-Римана не выполнены, зачастую на всей комплексной плоскости.
Хорошо, но тогда возникает ещё более интересный вопрос: а можно ли заранее узнать, что для функции ![]() существует «хорошая» функция
существует «хорошая» функция ![]() ? (чтобы выполнялись условия Коши-Римана). Можно! Для этого действительная часть должна быть непрерывна в рассматриваемой области и удовлетворять условию:
? (чтобы выполнялись условия Коши-Римана). Можно! Для этого действительная часть должна быть непрерывна в рассматриваемой области и удовлетворять условию:
![]() (это частные производные второго порядка, кто запамятовал).
(это частные производные второго порядка, кто запамятовал).
Такие функции называют гармоническими (загуглите самостоятельно). Проверим выполнение условия, скажем, для функции ![]() . Производные здесь устные:
. Производные здесь устные:
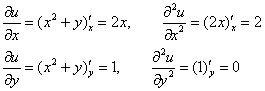
Таким образом: ![]() , значит, для функции
, значит, для функции ![]() не существует функции
не существует функции ![]() , такой, чтобы выполнялись условия Коши-Римана. Но мнимую часть можно придумать произвольно, и
, такой, чтобы выполнялись условия Коши-Римана. Но мнимую часть можно придумать произвольно, и ![]() будет совершенно законной функцией. Только с дифференцированием грусть.
будет совершенно законной функцией. Только с дифференцированием грусть.
Теперь проверим ![]() из Примера 2:
из Примера 2:
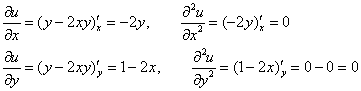
Таким образом: ![]() – для всех значений
– для всех значений ![]() , значит, для функции
, значит, для функции ![]() заведомо существует сопряжённая («хорошая») функция
заведомо существует сопряжённая («хорошая») функция ![]() , при этом условия Коши-Римана выполнены на всей комплексной плоскости, следовательно, функция
, при этом условия Коши-Римана выполнены на всей комплексной плоскости, следовательно, функция ![]() дифференцируема всюду. Дело за малым, решить Пример 2, что, я надеюсь, вы успешно сделали. Решаем, разбираемся, иначе тоже грусть.
дифференцируема всюду. Дело за малым, решить Пример 2, что, я надеюсь, вы успешно сделали. Решаем, разбираемся, иначе тоже грусть.
И, очевидно, справедлив «зеркальный» факт. Для функции ![]() существует сопряжённая функция
существует сопряжённая функция ![]() только в том случае, если выполнено условие
только в том случае, если выполнено условие ![]() . Не отходя от кассы, рассмотрим соответствующую задачу. Алгоритм, как уже упоминалось, будет очень похожим:
. Не отходя от кассы, рассмотрим соответствующую задачу. Алгоритм, как уже упоминалось, будет очень похожим:
Пример 3
Дана мнимая часть ![]() функции комплексной переменной. Выяснить, существует ли сопряжённая действительная часть
функции комплексной переменной. Выяснить, существует ли сопряжённая действительная часть ![]() , если – да, то найти её и функцию
, если – да, то найти её и функцию ![]() , удовлетворяющую начальному условию
, удовлетворяющую начальному условию ![]() .
.
Так как наличие «хорошей» действительной части не гарантировано, то к решению следует добавить дополнительный пункт:
0) Проверим, существует ли для ![]() сопряжённая функция
сопряжённая функция ![]() . Найдём частные производные второго порядка:
. Найдём частные производные второго порядка:
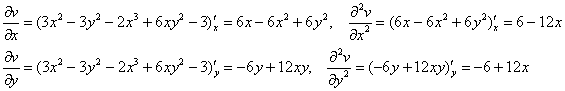
и их сумму:
![]() , значит, существует функция
, значит, существует функция ![]() , такая, что функция
, такая, что функция ![]() дифференцируема (т. е. такая, что условия Коши-Римана выполнены), причём в данном случае на всей комплексной плоскости.
дифференцируема (т. е. такая, что условия Коши-Римана выполнены), причём в данном случае на всей комплексной плоскости.
1) Согласно условиям Коши-Римана:
![]() – работаем с этой производной.
– работаем с этой производной.
![]() – про эту пока забываем.
– про эту пока забываем.
Поскольку ![]() , то действительная часть восстанавливается частным интегрированием по «икс». А если интегрируем по «икс», то «игрек» считается константой:
, то действительная часть восстанавливается частным интегрированием по «икс». А если интегрируем по «икс», то «игрек» считается константой:
![]() , где
, где ![]() – неизвестная функция, зависящая только от «игрек».
– неизвестная функция, зависящая только от «игрек».
Для проверки можно мысленно или на черновике найти частную производную:
![]() , что и требовалось проверить.
, что и требовалось проверить.
Берём недоделанную действительную часть ![]() и находим частную производную по «игрек»:
и находим частную производную по «игрек»:
![]() – результат приравниваем к «забытой» частной производной:
– результат приравниваем к «забытой» частной производной:
![]()
Таким образом, после сокращений:
![]()
Интегрированием восстанавливаем функцию ![]() :
:
![]()
В результате:
![]() – действительная часть функции
– действительная часть функции ![]() .
.
2) Найдем функцию ![]() :
:
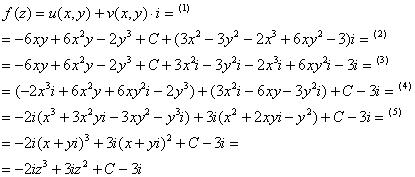
(1) Подставляем мнимую часть и найденную действительную часть.
(2) Раскрываем скобки.
(3) Снова выполняем перегруппировку слагаемых. Анализирую слагаемые, видим, что среди них есть слагаемые с кубами, а значит, дело сведётся к формуле ![]() . Поэтому в первой скобке группируем слагаемые, которые явно относятся к данной формуле. Аналогично – замечаем среди слагаемых слагаемые с квадратами, и во второй скобке группируем слагаемые, чтобы далее воспользоваться формулой
. Поэтому в первой скобке группируем слагаемые, которые явно относятся к данной формуле. Аналогично – замечаем среди слагаемых слагаемые с квадратами, и во второй скобке группируем слагаемые, чтобы далее воспользоваться формулой ![]() .
.
(4) Проводим вынесение за скобки множителей, чтобы внутри осталось, то, что нужно. При этом полезно мысленно или черновике сделать проверку, раскрыв скобки ![]() и
и ![]() .
.
(5) Запаковываем функцию.
В итоге получена функция ![]() , в которой присутствует только комплексная переменная «зет» и константы.
, в которой присутствует только комплексная переменная «зет» и константы.
3) В соответствии с начальным условием ![]() :
:
![]()
Ответ: ![]() ,
, ![]()
Готово. Примеры с кубами встречаются достаточно часто, поэтому набиваем руку:
Пример 4
Дана мнимая часть ![]() функции комплексной переменной. Убедиться, что для неё существует сопряжённая действительная часть
функции комплексной переменной. Убедиться, что для неё существует сопряжённая действительная часть ![]() , найти её и функцию
, найти её и функцию ![]() , удовлетворяющую начальному условию
, удовлетворяющую начальному условию ![]() .
.
Этот пример можно решить по шаблону только что разобранного примера. Но обратите внимание на отличие от предыдущего условия – тут утверждается, что такая часть существует. Примерный образец чистового оформления задания в конце урока. И для полного счастья пример, где дана действительная часть ![]() :
:
Пример 5
Для заданной функции ![]() найти сопряженную функцию
найти сопряженную функцию ![]() и функцию
и функцию ![]() при известном значении
при известном значении ![]() .
.
![]()
И вновь прочувствуем оттенки вкуса. Здесь тоже «между строк» подразумевается существование сопряжённой части, но в любом случае я рекомендую вам выполнять предварительную проверку. Чтобы не было мучительно больно за напрасное решение, в котором «ничего не сошлось».
Что делать, если по вине опечатки / коварства сопряжённой функции не существует? Для начала перепроверьте все частные производные и сумму производных второго порядка – а вдруг вы сами ошиблись? Если всё гладко, то оформляем на чистовик проверку и делаем соответствующий вывод: сопряжённой части не существует, а значит, не существует и требуемой функции ![]() .
.
В большинстве случаев вам встретится что-нибудь из уже рассмотренных заданий с квадратами да кубами, но время от времени попадаются более занятные примеры, для решения которых нам потребуется формула Эйлера:
![]()
и её версия для «минус альфа»:
![]()
Коль скоро мы рассматриваем обратную задачу, то данные формулы тоже будут применяться в обратном направлении:
![]()
Еще два, причём, не самых простых примера из реальных контрольных работ студентов:
Пример 6
Для заданной функции ![]() найти сопряженную функцию
найти сопряженную функцию ![]() и функцию
и функцию ![]() при заданном начальном условии.
при заданном начальном условии.
![]()
Решение: первый пункт алгоритма обкатан и стандартен:
1) Найдем мнимую часть функции ![]() . Так как
. Так как ![]() , то:
, то:
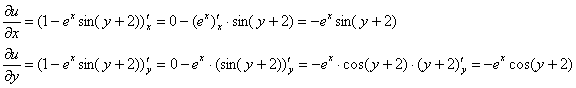
И от греха подальше убедимся (хотя бы на черновике), что сопряженная функция вообще существует:
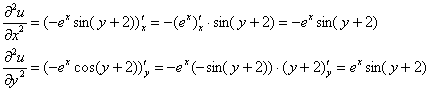
![]() , отлично, продолжаем.
, отлично, продолжаем.
В соответствии с условиями Коши-Римана (а когда дана действительная часть, их нужно сначала переписать в другом виде – см. Примеры № 1, 2):
![]() – работаем с этой производной;
– работаем с этой производной;
![]() – про эту производную пока забываем.
– про эту производную пока забываем.
Поскольку ![]() , то:
, то:
![]()
Найдём частную производную по «икс»:
![]() – результат приравниваем к «забытой» частной производной:
– результат приравниваем к «забытой» частной производной:
![]()
Сокращаем равенство и восстанавливаем функцию ![]() :
:
![]()
В результате:
![]() – мнимая часть функции
– мнимая часть функции ![]()
2) Второй пункт будет куда веселее. Составим функцию ![]() :
:
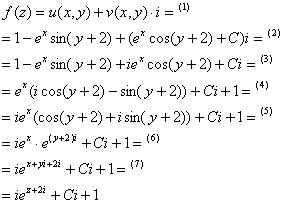
(1) Подставляем действительную и мнимую части.
(2) Раскрываем скобки.
(3) Выполняем перегруппировку слагаемых, при этом выносим ![]() за скобку.
за скобку.
(4) В скобках нужно организовать конструкцию ![]() , чтобы воспользоваться формулой Эйлера. Немного подумав, догадываемся, что нужно вынести за скобку мнимую единицу.
, чтобы воспользоваться формулой Эйлера. Немного подумав, догадываемся, что нужно вынести за скобку мнимую единицу.
(5) Используем формулу Эйлера ![]() , при этом
, при этом ![]()
(6) По школьному правилу действий со степенями подводим экспоненты под единый показатель. Попутно в показателе раскрываем скобки ![]()
(7) В показателе экспоненты проводим окончательную упаковку: ![]()
В результате получена вполне симпатичная функция ![]() , в которой присутствуют только комплексная переменная «зет» и константы.
, в которой присутствуют только комплексная переменная «зет» и константы.
3) Найдём значение константы ![]() …, кто-нибудь ещё помнит об этом маленьком третьем этапе? =) В соответствии с начальным условием
…, кто-нибудь ещё помнит об этом маленьком третьем этапе? =) В соответствии с начальным условием ![]() :
:
![]()
Таким образом: ![]()
Ответ: ![]() ,
, ![]()
Погорячился я со сложностью, на самом деле пример был довольно прост. Но ничего страшного, я привык исполнять обещания, держите:
Пример 7
Для заданной функции ![]() найти сопряженную функцию
найти сопряженную функцию ![]() и функцию
и функцию ![]() при заданном начальном условии.
при заданном начальном условии.
![]()
В предложенном примере дана мнимая часть функции, поэтому придерживаемся алгоритма Примеров № 3, 4. Задание технически сложное, потребуются хорошие навыки нахождения частных производных, а на втором этапе нужно будет догадаться, как распутать клубок и применить формулу Эйлера. Однако пример взят из реальной контрольной работы студента заочного отделения. Полное решение и ответ внизу.
На первом уроке также были представлены формулы для синуса и косинуса:
![]()
Но обратной задачи по этим формулам мне ни разу не встречалось. Тем не менее, я воодушевился предыдущим примером, на лице появилась добрая улыбка, а душа прям-таки требует рассказать вам ещё какую-нибудь гадость. Поэтому в заключение разберу любопытный пример, который не так давно встретился в моей практике.
Пример 8
Восстановить функцию ![]() по известной мнимой части
по известной мнимой части ![]() и значению
и значению ![]() .
.
Условие опять немного перефразировано, но вы уже универсальные бойцы :)
Решение: 1) Найдем действительную часть функции ![]() .
.
Нарезаем частные производные от ![]() :
:
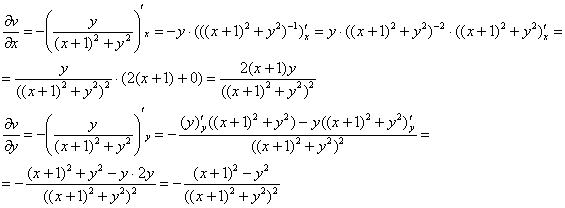
И тут проверку ![]() что-то выполнять неохота, поэтому поверим автору задачи :)
что-то выполнять неохота, поэтому поверим автору задачи :)
В соответствии с условиями Коши-Римана:
![]() – работаем с этой производной;
– работаем с этой производной;
![]() – про эту пока забываем.
– про эту пока забываем.
Если ![]() , то:
, то:
![]()
…и на этом этапе стандартного алгоритма я крепко задумался. Превратил мысленно «игреки» в константы, и пришёл к выводу, что интеграл, конечно, берётся…. Но является довольно сложным с неприятным и долгим решением. Кстати, похожие штуковины рассмотрены в статье Сложные интегралы.
Что делать? Есть другая возможность!
![]() – про эту производную пока забываем;
– про эту производную пока забываем;
![]() – работаем с этой производной.
– работаем с этой производной.
То есть восстановление действительной части пытаемся начать с другой частой производной, вдруг интеграл проще получится?
Если ![]() , то:
, то:
![]()
И действительно, интеграл получился намного более простым! Здесь я использовал метод подведения функции под знак дифференциала (не забывайте, что «икс» – константа!).
Находим частную производную по «икс» от недоделанной действительной части:
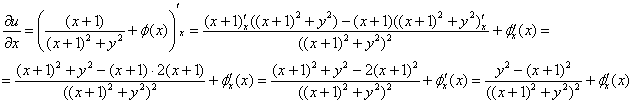
Приравниваем результат к «забытой» частной производной:
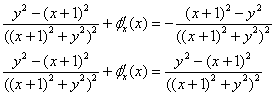
Страшные дроби благополучно сократились и:
![]()
Таким образом: ![]() – действительная часть функции
– действительная часть функции ![]() .
.
2) Найдем функцию ![]() :
:
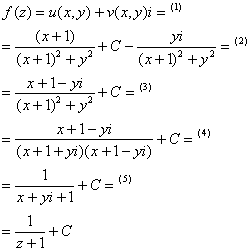
(1) Поставляем действительную и мнимую части.
(2) Знаменатели дробей одинаковы, поэтому оформляем дроби под единым знаменателем.
(3) Раскладываем знаменатель на множители при помощи формулы разности квадратов: ![]() . Конечно, это не совсем очевидно, особенно для чайника. И для сомневающихся читателей выполню проверку:
. Конечно, это не совсем очевидно, особенно для чайника. И для сомневающихся читателей выполню проверку:
![]()
(4) Сокращаем дробь на ![]() .
.
(5) Упаковываем функцию: ![]() .
.
Готово: ![]()
3) В соответствии с начальным условием: ![]()
Таким образом: ![]() – искомая функция.
– искомая функция.
Ответ: ![]() ,
, ![]()
Вот так вот иногда бывает. Казалось бы, такая простенькая функция ![]() , а сколько приключений! Никогда не нужно теряться – если дверь закрыта, пробуйте залезть в форточку! И не забывайте, я в доле =)
, а сколько приключений! Никогда не нужно теряться – если дверь закрыта, пробуйте залезть в форточку! И не забывайте, я в доле =)
Желаю успехов!
Решения и ответы:
Пример 2. Решение:
1) Найдём мнимую часть ![]() . Частные производные от действительной части:
. Частные производные от действительной части:
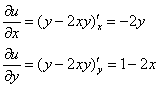
В соответствии с условиями Коши-Римана:
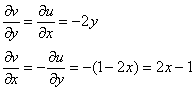
Поскольку ![]() , то:
, то:
![]()
![]()
Таким образом:
![]()
![]()
В результате:
![]() – мнимая часть функции
– мнимая часть функции ![]()
2) Найдем функцию ![]() :
:
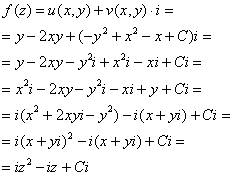
3) В соответствии с начальным условием ![]() :
:
![]()
Ответ: ![]() ,
, ![]()
Пример 4. Решение: проверим, существует ли для ![]() сопряженная функция. Найдём частные производные второго порядка:
сопряженная функция. Найдём частные производные второго порядка:
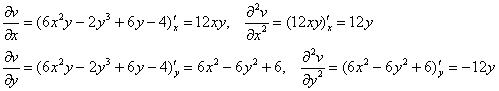
Таким образом: ![]() , значит, сопряжённая функция существует.
, значит, сопряжённая функция существует.
Найдем действительную часть функции ![]() . В соответствии с условиями Коши-Римана:
. В соответствии с условиями Коши-Римана:
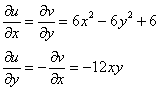
Поскольку ![]() , то:
, то:
![]()
Найдём частную производную по «игрек»:
![]()
Таким образом:
![]()
![]() , следовательно,
, следовательно, ![]()
В результате:
![]() – действительная часть функции
– действительная часть функции ![]() .
.
Найдем функцию ![]() :
:
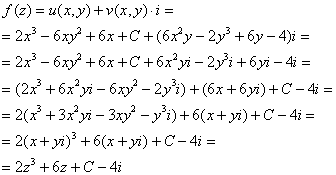
В соответствии с начальным условием ![]() :
:
![]()
Ответ: ![]() ,
, ![]()
Пример 5. Решение: найдем мнимую часть функции ![]() .
.
Возьмём частные производные от ![]() :
:
![]()
! Контроль: ![]() , ОК.
, ОК.
В соответствии с условиями Коши-Римана:
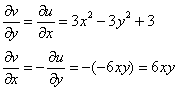
Так как ![]() , то:
, то:
![]()
![]()
Таким образом:
![]()
![]()
В результате: ![]() – мнимая часть функции
– мнимая часть функции ![]() .
.
Найдем функцию ![]() :
:
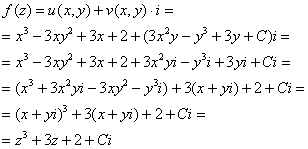
В соответствии с начальным условием: ![]() .
.
Ответ: ![]() ,
, ![]() – искомая функция.
– искомая функция.
Пример 7. Решение: найдем действительную часть функции ![]() .
.
Так как ![]() , то:
, то:
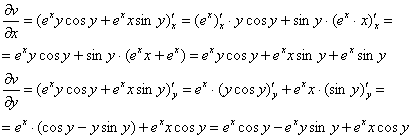
Проверку ![]() проведите самостоятельно.
проведите самостоятельно.
В соответствии с условиями Коши-Римана:

Поскольку ![]() , то:
, то:
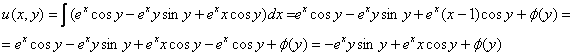
Примечание: интеграл ![]() берётся по частям.
берётся по частям.
Найдём частную производную по «игрек»:
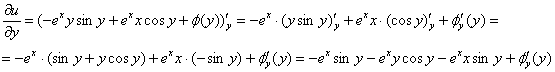
Таким образом:
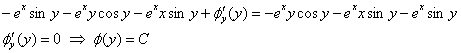
В результате:
![]() – действительная часть функции
– действительная часть функции ![]() .
.
Найдем функцию ![]() :
:
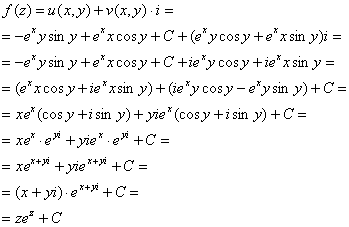
В соответствии с начальным условием ![]() :
:
![]()
Ответ: ![]() ,
, ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright