


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как вычислить двойной интеграл? Примеры решений
Прозвучал удар гонга, который открывает второй раунд в бою с двойными интегралами. Если вы недавно надели перчатки или вообще боксируете с грушей, то, пожалуйста, начните с первого раунда Двойные интегралы для чайников. Настоятельно рекомендую разобраться со всеми примерами вводного урока без халтуры, это очень важно. К тому же, добрый дядя Саша нарисовал много картинок, которые можно распечатать и наклеить у себя в туалете. Помните, что Коперник свои блестящие открытия в астрономии делал именно там.
Однако задорное получилось вступление…. Задумался вот… почему? Да потому что мне хорошо. А отчего хорошо, поясню в конце статьи.
Вспоминаем общую запись двойного интеграла:
![]()
В первой статье Двойные интегралы для чайников я очень подробно рассмотрел понятие двойного интеграла, алгоритм его решения, важнейшие задачи на обход области интегрирования. Также были прорешаны простейшие двойные интегралы в примерах на нахождение площади плоской фигуры.
Снова посмотрим на общую запись двойного интеграла и заметим, что в нём притаилась функция двух переменных ![]() . А когда речь заходит о функции двух переменных, то это часто попахивает частными производными второго порядка. Поэтому для освоения примеров вам нужно уметь более или менее уверенно их находить.
. А когда речь заходит о функции двух переменных, то это часто попахивает частными производными второго порядка. Поэтому для освоения примеров вам нужно уметь более или менее уверенно их находить.
В большинстве практических задач требуется формально вычислить двойной интеграл, но, помимо этого, он обладает отличным геометрическим смыслом – с помощью двойного интеграла помимо площади можно вычислить еще и объём. Геометрический смысл двойного интеграла поясню ниже на конкретных примерах.
Начинаем набивать наш двойной интеграл ![]() разнообразной начинкой:
разнообразной начинкой:
Пример 1
Вычислить двойной интеграл
![]() ,
, ![]()
Изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Решение: Изобразим область интегрирования ![]() на чертеже:
на чертеже:
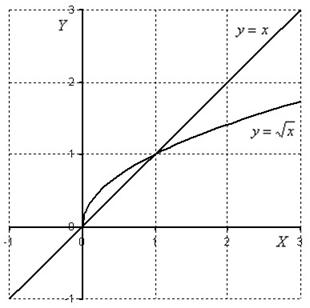
Напоминаю, что выполнение чертежа – это строго показанный начальный этап решения. Чертёж крайне важно выполнить правильно и точно, поскольку ошибка в графике незамедлительно запорет всё задание.
Выберем следующий порядок обхода:
![]()
Вопросы порядка обхода области интегрирования, я комментировать практически не буду, пожалуйста, смотрите статью Двойные интегралы для чайников.
Таким образом:
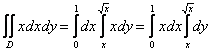
Обратите внимание на следующее действие: в данном случае можно вынести «икс» из внутреннего интеграла во внешний интеграл. Почему? Во внутреннем интеграле ![]() интегрирование проводится по «игрек», следовательно, «икс» считается константой. А любую константу можно вынести за знак интеграла, что благополучно и сделано.
интегрирование проводится по «игрек», следовательно, «икс» считается константой. А любую константу можно вынести за знак интеграла, что благополучно и сделано.
С интегралами настоятельно рекомендую разбираться по пунктам:
1) Используя формулу Ньютона-Лейбница, найдём внутренний интеграл:
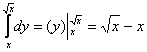
Вместо «игрека» подставляем функции!
2) Результат, полученный в первом пункте, подставим во внешний интеграл ![]() , при этом ни в коем случае не забываем про «икс», который там уже находится:
, при этом ни в коем случае не забываем про «икс», который там уже находится:
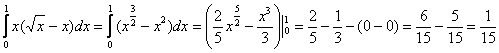
Готово.
Замечательно, если у вас под рукой есть микрокалькулятор, на котором можно считать обыкновенные дроби, он значительно ускорит заключительные вычисления. В последующих примерах я не буду подробно расписывать приведение дробей к общему знаменателю, а просто запишу ответ.
Выполняем вторую часть задания: изменим порядок обхода области и вычислим двойной интеграл вторым способом.
Перейдём к обратным функциям:
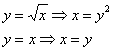
Для наглядности еще раз приведу чертёж, он будет точно таким же, но с другими обозначениями графиков:
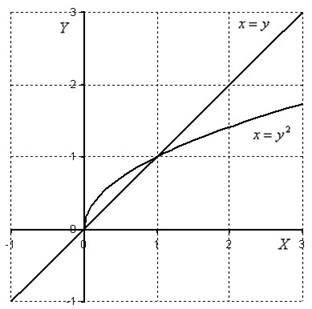
Второй способ обхода области:
![]()
Таким образом:
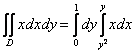
Вот здесь уже «икс» является «родным» для внутреннего интеграла, поэтому его нельзя вынести во внешний интеграл.
1) Используя формулу Ньютона-Лейбница, вычислим внутренний интеграл:
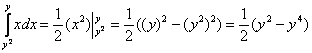
Вместо «икса» подставляются функции!
Всегда проявляйте повышенное внимание при подстановке пределов интегрирования.
2) Результат, полученный в первом пункте, подставим во внешний интеграл и проведём окончательные вычисления:
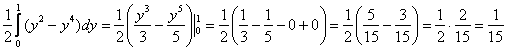
Результаты совпали, значит, задание выполнено верно.
Если есть время, постарайтесь всегда проводить проверку, даже если этого не требуется в условии: вычислили интеграл одним способом – затем изменили порядок обхода области и вычислили вторым способом.
Ответ: ![]()
Пример 2
Вычислить двойной интеграл
![]() ,
, ![]()
Выполнить проверку: изменить порядок интегрирования и вычислить двойной интеграл вторым способом.
Это пример для самостоятельного решения. Обратите внимание, что в двойном интеграле изначально присутствует константа. А константу можно вынести за знак двойного интеграла, в данном случае:
![]()
В ходе решения вынесение константы целесообразно проводить в момент перехода к повторным интегралам.
Как видите, свойство линейности справедливо не только для «обычных», но и для кратных интегралов. Интеграл от интеграла недалеко падает.
Самое главное потом при вычислениях вынесенную константу не потерять. А забывают о ней часто.
Примерный образец чистового оформления примера в конце урока.
Двойной интеграл как объем тела
Рассмотрим основной геометрический смысл двойного интеграла ![]() . Предполагаем, что функция
. Предполагаем, что функция ![]() существует в каждой точке
существует в каждой точке ![]() плоской области
плоской области ![]() и задаёт некоторую поверхность трехмерного пространства. Для определенности считаем, что
и задаёт некоторую поверхность трехмерного пространства. Для определенности считаем, что ![]() , то есть поверхность располагается над плоскостью
, то есть поверхность располагается над плоскостью ![]() .
.
Согласно общей концепции интегрирования, произведение ![]() равно бесконечно малому объёму
равно бесконечно малому объёму ![]() элементарного кусочка тела (посмотрите на кусок, выделенный на чертеже пунктирными линиями, и мысленно сделайте бесконечно малыми его «длину» и «ширину»). Двойной же интеграл объединяет эти бесконечно малые значения
элементарного кусочка тела (посмотрите на кусок, выделенный на чертеже пунктирными линиями, и мысленно сделайте бесконечно малыми его «длину» и «ширину»). Двойной же интеграл объединяет эти бесконечно малые значения ![]() по всей области
по всей области ![]() , в результате чего мы получаем суммарный (интегральный) объём всего цилиндрического бруса
, в результате чего мы получаем суммарный (интегральный) объём всего цилиндрического бруса ![]() :
:
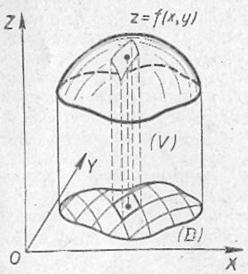
Что это за тело, думаю, понятно – снизу цилиндрический брус ограничен заштрихованной областью ![]() , а сверху – фрагментом поверхности
, а сверху – фрагментом поверхности ![]() («шапкой»).
(«шапкой»).
Дополнительно поясню геометрический смысл на Примере № 1. В нём мы рассматривали двойной интеграл ![]() , причём область интегрирования имела следующий вид:
, причём область интегрирования имела следующий вид:

Из начала координат перпендикулярно экрану монитора мысленно проведите на себя стрелку оси ![]() . Подынтегральная функция
. Подынтегральная функция ![]() задаёт плоскость в пространстве, которая проходит над областью
задаёт плоскость в пространстве, которая проходит над областью ![]() и ограничивает цилиндрический брус сверху, поэтому значение его объёма получилось положительным:
и ограничивает цилиндрический брус сверху, поэтому значение его объёма получилось положительным: ![]() . Да, такой вот малюсенький брусок, 1/15-я единичного «кубика».
. Да, такой вот малюсенький брусок, 1/15-я единичного «кубика».
Двойной интеграл может быть и отрицательным, в таких случаях график функции ![]() полностью (или бОльшей частью) лежит под областью
полностью (или бОльшей частью) лежит под областью ![]() . И если в задаче требуется найти именно объём тела с помощью двойного интеграла (в тройном этот вопрос отпадает), то к «кускам», лежащим ниже плоскости
. И если в задаче требуется найти именно объём тела с помощью двойного интеграла (в тройном этот вопрос отпадает), то к «кускам», лежащим ниже плоскости ![]() , следует добавить знак «минус» (по аналогии с площадью криволинейной трапеции, лежащей ниже оси абсцисс).
, следует добавить знак «минус» (по аналогии с площадью криволинейной трапеции, лежащей ниже оси абсцисс).
Однако на практике почти всегда встречаются задачи на формальный расчёт двойных интегралов, поэтому мы продолжим совершенствовать технику вычислений:
Пример 3
Вычислить двойной интеграл
![]() ,
, ![]()
Решение: Изобразим область интегрирования на чертеже:
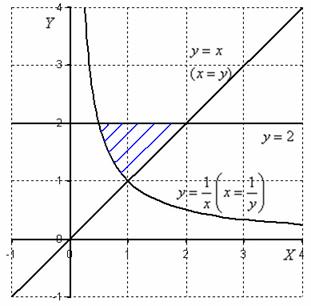
После того, как корректно выполнен чертеж и правильно найдена область интегрирования, самое время разобраться с порядком обхода.
Согласно первому способу обхода, область придется разделить на две части, при этом нужно будет вычислить следующие интегралы:
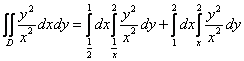
Энтузиазма, прямо скажем, мало. Проанализируем, а не проще ли использовать второй способ обхода области? Перейдем к обратным функциям, переход здесь элементарен:
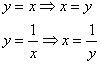
Порядок обхода области:
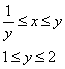
Таким образом:
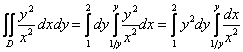
Ну вот, совсем другое дело. И снова заметьте, что во внутреннем интеграле интегрирование осуществляется по «икс», поэтому константу ![]() можно сразу вынести во внешний интеграл
можно сразу вынести во внешний интеграл
1) Найдём внутренний интеграл:
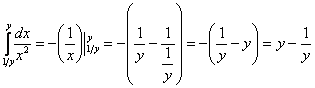
Всё-таки подстановка пределов интегрирования, порой, выглядит своеобразно. Сначала вместо «икса» мы подставили верхний предел интегрирования ![]() , затем вместо «икса» подставили нижний предел интегрирования
, затем вместо «икса» подставили нижний предел интегрирования ![]() . Будьте внимательны при подстановках!
. Будьте внимательны при подстановках!
2) Результат предыдущего пункта подставим во внешний интеграл, при этом не забываем про ![]() , который там уже находится:
, который там уже находится:
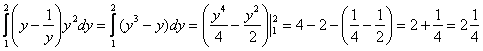
Ответ: ![]()
Для тренировки можете попробовать вычислить двойной интеграл менее рациональным способом: 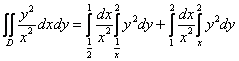 . Результаты должны совпасть.
. Результаты должны совпасть.
Пример 4
Вычислить двойной интеграл
![]() ,
, ![]()
Это пример для самостоятельного решения. Постройте область ![]() и проанализируйте, какой способ обхода области выгоднее использовать. Полное решение и ответ в конце урока.
и проанализируйте, какой способ обхода области выгоднее использовать. Полное решение и ответ в конце урока.
Усложняем задачу, теперь подынтегральная функция будет представлять собой сумму. Рассмотрим еще два примера, где я остановлюсь на приёме вычисления интеграла, который типичен и эффективен для кратных интегралов:
Пример 5
Вычислить двойной интеграл
![]() ,
, ![]()
Решение: Сначала рассмотрим то, чего делать не нужно – в данном случае не следует использовать свойство линейности кратного интеграла и представлять его в виде:
![]()
Почему? Вычислений заметно прибавится!
Решение, как обычно, начинаем с построения области интегрирования:
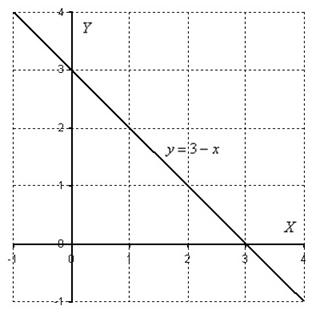
Область ![]() незамысловата, даже штриховать не буду. В данном примере, как легко заметить, не имеет особого значения порядок интегрирования, поэтому выберем первый, более привычный вариант обхода области:
незамысловата, даже штриховать не буду. В данном примере, как легко заметить, не имеет особого значения порядок интегрирования, поэтому выберем первый, более привычный вариант обхода области:
![]()
Таким образом:
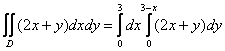
Здесь, в отличие от двух предыдущих примеров, из внутреннего интеграла ничего вынести нельзя, поскольку начинкой является сумма.
С повторными интегралами опять разбираемся по отдельности. Да, кстати, кто хочет посмотреть, как решать повторные интегралы одной строкой, пожалуйста, зайдите на страницу Готовые решения по высшей математике и закачайте архив с примерами решений кратных интегралов.
1) Сначала берём внутренний интеграл:
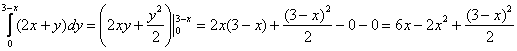
Хотелось бы остановиться на нескольких существенных моментах. Во-первых, о частном интегрировании. О нём я уже подробно рассказывал в статье Дифференциальные уравнения в полных дифференциалах. Вкратце повторюсь:
Если интегрирование проводится по «игрек», то переменная «икс» считается константой. И наоборот.
Тем не менее, вот нашли вы первообразную ![]() и возникли сомнения, а правильно ли она найдена? Всегда можно выполнить проверку, в данном случае следует найти частную производную по «игрек»:
и возникли сомнения, а правильно ли она найдена? Всегда можно выполнить проверку, в данном случае следует найти частную производную по «игрек»:
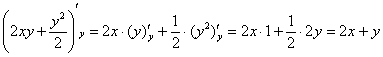
Получена исходная подынтегральная функция, значит, всё в порядке.
Момент второй, подстановка пределов интегрирования. По стандартной формуле Ньютона-Лейбница сначала вместо «игреков» мы подставили ![]() , а затем – нижний предел интегрирования (нули). После подстановки должны остаться только «иксы».
, а затем – нижний предел интегрирования (нули). После подстановки должны остаться только «иксы».
И, наконец, может показаться странным результат: ![]()
Ведь можно раскрыть скобки и привести подобные слагаемые! В данном случае это сделать несложно, и чайникам, вероятно, лучше так и поступить. Но если будет не вторая, а 3-я или 4-я степень? На самом деле линейную функцию в степени выгоднее проинтегрировать, не раскрывая скобок! Данный прием я уже применял и подробно комментировал во втором параграфе урока Как вычислить объем тела вращения?
Ещё раз посмотрим, как он работает:
2) Берём оставшийся внешний интеграл:

При нахождении интеграла 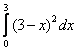 использован метод подведения функции под знак дифференциала. Где-нибудь возникли сомнения в правильности интегрирования? Возьмите производную по «икс» и выполните проверку!
использован метод подведения функции под знак дифференциала. Где-нибудь возникли сомнения в правильности интегрирования? Возьмите производную по «икс» и выполните проверку!
Ответ: ![]()
Пример 6
Вычислить двойной интеграл
![]() ,
, ![]()
Это пример для самостоятельного решения. В образце решения, как и в разобранном примере, использован первый способ обхода области.
На практике немало примеров, где трудно (а то и невозможно) обойтись без микрокалькулятора-«дробовика». Рассмотрим практический пример на данную тему:
Пример 7
Вычислить двойной интеграл по области ![]()
![]()
Задача будет решена двумя способами, так как готовое решение у меня уже есть =) А если серьезно, второй способ будет нужен для дополнительных важных комментариев.
Решение: Изобразим область интегрирования на чертеже:
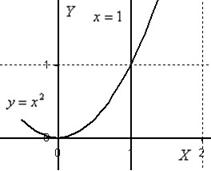
Область интегрирования тут простая, и основной гемор ожидается как раз в вычислениях.
Выберем следующий порядок обхода области:
![]()
Таким образом:
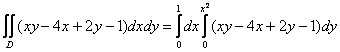
1) 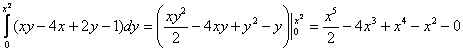
Начинающим чайникам всегда рекомендую выполнять проверку, особенно в подобных примерах: возьмите частную производную по «игрек» от первообразной ![]() и получите подынтегральную функцию
и получите подынтегральную функцию ![]() .
.
Будьте предельно внимательны в подстановке пределов интегрирования: сначала вместо «игреков» подставляем ![]() , затем – ноль. В оформлении вполне допустимо записать один, а не несколько нолей, как это сделано в данном примере. После подстановки должны остаться только «иксы».
, затем – ноль. В оформлении вполне допустимо записать один, а не несколько нолей, как это сделано в данном примере. После подстановки должны остаться только «иксы».
2) Второй шаг прост:
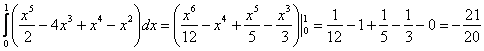
Перейдём к обратной функции ![]() и изменим порядок обхода области:
и изменим порядок обхода области:
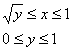
Таким образом:
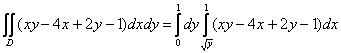
1) Вычислим внутренний интеграл:
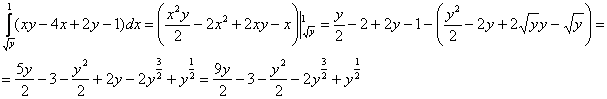
Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Не лишней будет и промежуточная проверка, возьмём частную производную по «икс» от найденной первообразной:
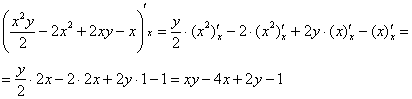
Получена подынтегральная функция, что и хотелось увидеть.
Подстановка пределов интегрирования здесь сложнее: сначала вместо «иксов» подставляем 1, затем вместо «иксов» подставляем ![]() . После подстановки должны остаться только «игреки».
. После подстановки должны остаться только «игреки».
Степени рекомендую оставить в виде ![]() , а не преобразовывать их в корни – будет удобнее интегрировать на втором шаге:
, а не преобразовывать их в корни – будет удобнее интегрировать на втором шаге:
2)
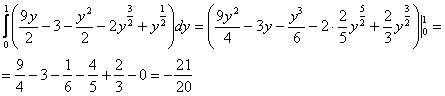
Результаты совпали, как оно и должно быть.
Легко заметить, что первый способ решения был заметно проще.
Всегда перед решением анализируйте – какой путь легче и короче.
Дроби в рассмотренном примере еще худо-бедно можно привести к общему знаменателю вручную. Но не удивляйтесь, если на практике получится ответ вроде ![]() , по крайне мере, в своей коллекции я нашел немало диких примеров, где без калькулятора-«дробовика» фактически не обойтись.
, по крайне мере, в своей коллекции я нашел немало диких примеров, где без калькулятора-«дробовика» фактически не обойтись.
Ответ: ![]()
Ответ получился отрицательным. Геометрически это обозначает, что график подынтегральной функции ![]() (поверхность в пространстве) полностью или бОльшей частью (не проверял) располагается ниже области интегрирования
(поверхность в пространстве) полностью или бОльшей частью (не проверял) располагается ниже области интегрирования ![]() под плоскостью
под плоскостью ![]() .
.
Пример 8
Вычислить двойной интеграл по области ![]()
![]()
Это пример для самостоятельного решения. Ответ будет целым – чтобы от своего хорошего настроения не запугать вас окончательно =). Похожие двойные интегралы встречаются в известном задачнике Кузнецова, и по этой причине пример тоже уместен. Полное решение и ответ в конце урока.
Студенты-заочники почти всегда сталкиваются с двойными интегралами наподобие тех, которые уже рассмотрены, но никто не застрахован от творческих примеров, где в подынтегральной функции есть какие-нибудь синусы, косинусы, экспоненты и т.п.
Рассмотрим заключительные примеры на данную тему:
Пример 9
Вычислить двойной интеграл по области ![]()
![]()
Решение: В ходе выполнения чертежа может возникнуть трудность с построением прямой ![]() , которая параллельна оси
, которая параллельна оси ![]() . Ничего сложного: если
. Ничего сложного: если ![]() , то
, то ![]() – примерно на этом уровне и следует провести прямую.
– примерно на этом уровне и следует провести прямую.
Выполним чертёж:
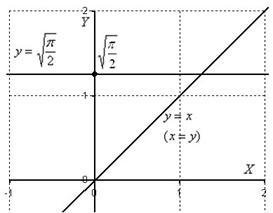
После выполнения чертежа нужно выяснить, какой порядок обхода области выгоднее применить.
Рассмотрим первый способ обхода:
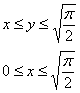
Тогда: 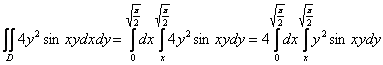
Очевидно, что первый способ является крайне неудачным, поскольку внутренний интеграл  придётся дважды брать по частям.
придётся дважды брать по частям.
Но есть еще и второй способ обхода области:
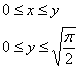
Следовательно: 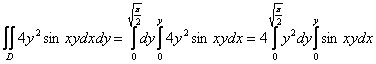
Выглядит гораздо привлекательнее, начинаем вычисления:
1) По формуле Ньютона-Лейбница разберемся с внутренним интегралом:
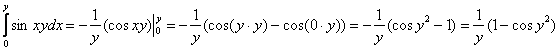
Когда мы интегрируем по «икс», то переменная «игрек» считается константой. Если возникают трудности с интегрированием, можно прибегнуть даже к такому способу: временно замените «игрек» конкретным числом, например, «пятёркой»:
![]() .
.
Теперь замените «пятёрку» обратно – «игреком»: ![]()
И, конечно же, лучше сделать проверку, продифференцировав первообразную по «икс»:
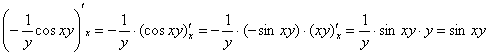
Далее при подстановке пределов интегрирования сначала вместо «икса» подставляем ![]() , затем – ноль. После подстановки должны остаться только «игреки».
, затем – ноль. После подстановки должны остаться только «игреки».
2) Полученный результат ![]() перемещаем во внешний интеграл, не забывая, что там уже есть
перемещаем во внешний интеграл, не забывая, что там уже есть ![]() и константа 4:
и константа 4:

Второй интеграл взят методом подведения функции под знак дифференциала.
Ответ: ![]()
Таким образом, выбор порядка обхода иногда зависит не только от самой области интегрирования, но и от подынтегральной функции.
Пример 10
Вычислить двойной интеграл по области ![]()
![]()
Это пример для самостоятельного решения.
Хочется привести ещё примеры, но в первом раунде я обещал не маньячить, поэтому скрепя сердце, заканчиваю статью. Множество других примеров на вычисление двойных интегралов можно найти в соответствующем архиве на странице Готовые решения по высшей математике. Если тема проработана качественно, то рискну предположить, что многие читатели без особого труда разберутся и и в тройных интегралах – принципы решения очень похожи!
И напоследок раскрою обещанный секрет – так почему же мне сегодня хорошо?
Я много раз высказывал своим ученикам эту мудрую мысль, но они почему-то смеялись:
Хорошо должно быть каждый день!
Решения и ответы:
Пример 2: Решение: Изобразим область ![]() на чертеже:
на чертеже:
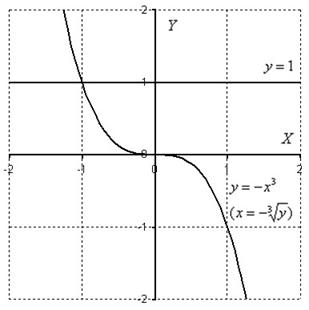
Выберем следующий порядок обхода:
![]()
Таким образом:
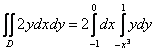
1) 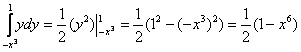
2) 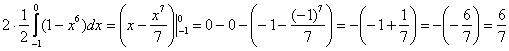
Перейдём к обратным функциям:
![]()
Изменим порядок обхода области:
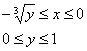
Таким образом:
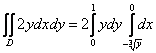
1) 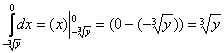
2) 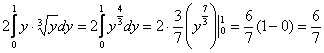
Ответ: ![]()
Пример 4: Решение: Изобразим область интегрирования на чертеже.
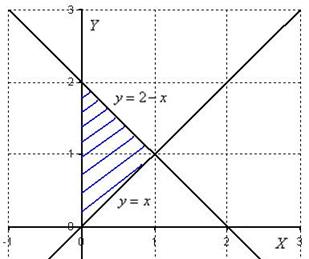
Выберем следующий порядок обхода области:
![]()
Таким образом:
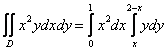
1) 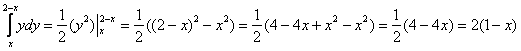 ;
;
2) 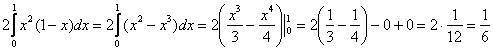
Ответ: ![]()
Пример 6: Решение: Изобразим область интегрирования на чертеже:
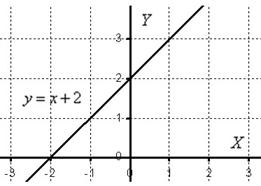
Выберем следующий порядок обхода области:
![]()
Таким образом:
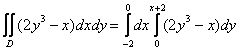
1) 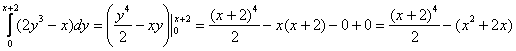
2)
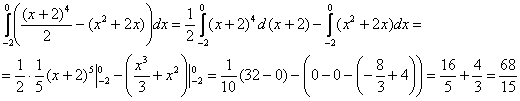
Ответ: ![]()
Пример 8: Решение: Изобразим область интегрирования на чертеже:
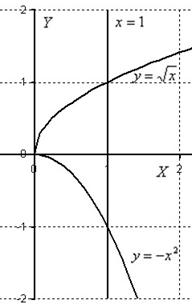
Выберем следующий порядок обхода области:
![]()
Таким образом:
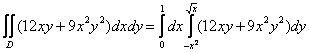
1) 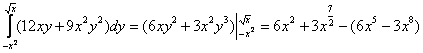
2) 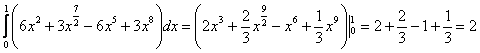
Ответ: ![]()
Пример 10: Решение: Изобразим область интегрирования на чертеже:
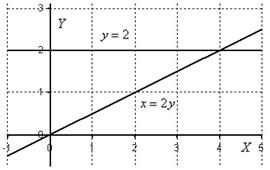
Выберем следующий порядок обхода области:
![]()
Таким образом:
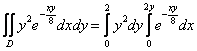
1) 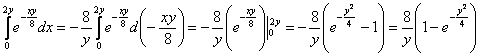
2)

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright