


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Дивергенция векторного поля.
Формула Гаусса-Остроградского
Данный урок представляет собой прямое продолжение статьи Поток векторного поля, и поэтому если вы зашли с поисковика, то, пожалуйста, начните с первой части, где мы подробно разобрали и решили важную задачу. А именно нашли поток векторного поля ![]() через замкнутую поверхность в направлении её внешней нормали:
через замкнутую поверхность в направлении её внешней нормали:
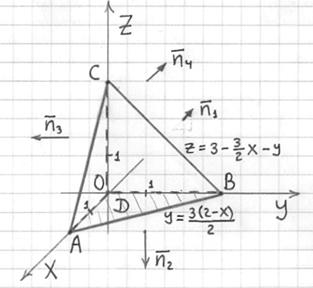
В ходе длинного-длинного решения нами был получен ответ ![]() , что в рамках условной гидродинамической модели означает следующее: сколько жидкости в единицу времени поступило в пирамиду – столько из неё и вытекло.
, что в рамках условной гидродинамической модели означает следующее: сколько жидкости в единицу времени поступило в пирамиду – столько из неё и вытекло.
Однако так бывает далеко не всегда, и на практике поток часто получается положительным или отрицательным. Задумаемся над содержательным смыслом этих результатов и для бОльшей наглядности рассмотрим не пирамиду, а кусок ![]() реки, ограниченный внешне-ориентированной поверхностью
реки, ограниченный внешне-ориентированной поверхностью ![]() и поле скоростей
и поле скоростей ![]() этой реки в области
этой реки в области ![]() .
.
Предположим, что поток через замкнутую поверхность ![]() оказался положителен:
оказался положителен: ![]() . Что это означает? Это означает, что за единицу времени из области
. Что это означает? Это означает, что за единицу времени из области ![]() жидкости вытекло БОЛЬШЕ, чем туда поступило. Следовательно, в области где-то есть источник(и) поля. Это может быть, например, приток реки, который увеличивает её скорость, или просто кто-то вылил ведро воды.
жидкости вытекло БОЛЬШЕ, чем туда поступило. Следовательно, в области где-то есть источник(и) поля. Это может быть, например, приток реки, который увеличивает её скорость, или просто кто-то вылил ведро воды.
Отрицательное значение потока ![]() через замкнутую поверхность
через замкнутую поверхность ![]() говорит нам о том, что за единицу времени область
говорит нам о том, что за единицу времени область ![]() «поглотила» жидкость (зашло больше, чем вышло). И причина тому – сток(и) поля в данной области. Например, подземная пещера или насос, выкачивающий воду.
«поглотила» жидкость (зашло больше, чем вышло). И причина тому – сток(и) поля в данной области. Например, подземная пещера или насос, выкачивающий воду.
И, наконец, при нулевом потоке ![]() возможны две ситуации: либо в области
возможны две ситуации: либо в области ![]() нет источников и стоков, либо они компенсируют друг друга.
нет источников и стоков, либо они компенсируют друг друга.
К слову, взаимная компенсация чаще всего имеет место и в первых двух случаях. Так, например, если ![]() , то это ещё не значит, что стоков нет. Возможно, источники оказались мощнее, и по итогу за единицу времени через поверхность выплеснулось 5 единиц жидкости.
, то это ещё не значит, что стоков нет. Возможно, источники оказались мощнее, и по итогу за единицу времени через поверхность выплеснулось 5 единиц жидкости.
И поэтому появляется интерес выяснить, есть ли у векторного поля ![]() источники / стоки, и если есть – то где. И в этом нам поможет
источники / стоки, и если есть – то где. И в этом нам поможет акваланг хитрая наука под названием математический анализ.
Рассмотрим некоторую точку ![]() области
области ![]() и её бесконечно малую замкнутую окрестность (например, сферу или куб). Поток векторного поля
и её бесконечно малую замкнутую окрестность (например, сферу или куб). Поток векторного поля ![]() через поверхность этой окрестности во внешнем направлении называется дивергенцией поля в данной точке, и обозначается через
через поверхность этой окрестности во внешнем направлении называется дивергенцией поля в данной точке, и обозначается через ![]() . И вот тут-то уж никуда не деться от разоблачения:
. И вот тут-то уж никуда не деться от разоблачения:
– если ![]() , то у векторного поля
, то у векторного поля ![]() есть источник в данной точке (её бесконечно малой окрестности);
есть источник в данной точке (её бесконечно малой окрестности);
– если ![]() , то сток;
, то сток;
– и если ![]() , то в точке
, то в точке ![]() нет источников и стоков.
нет источников и стоков.
Далее. Как найти эту самую дивергенцию? Если в каждой точке ![]() области
области ![]() определено векторное поле
определено векторное поле ![]() и его компоненты
и его компоненты ![]() дифференцируемы в этих точках, то скалярная функция дивергенции имеет следующий вид:
дифференцируемы в этих точках, то скалярная функция дивергенции имеет следующий вид:
![]() или, как записывают короче:
или, как записывают короче: ![]()
Таким образом, в области ![]() векторному полю
векторному полю ![]() ставится в соответствие скалярное поле
ставится в соответствие скалярное поле ![]() его дивергенции.
его дивергенции.
И здесь сразу можно выделить особый случай. Поле, дивергенция которого равна нулю ВО ВСЕХ точках области, называется бездивергентным или соленоидальным. Это означает, что у него нет источников и стоков. В качестве примера часто приводят трубу-«бублик» с циркулирующей водой, которая никуда не исчезает, и новой воды там не появляется. Но ещё более показательный пример – это магнитное поле с его замкнутыми силовыми линиями, у которых нет начала и конца.
Хорошо. Функция ![]() позволяет нам вычислить дивергенцию в отдельно взятых точках, и возникает вопрос: а можно ли подсчитать суммарную дивергенцию по всему телу?
позволяет нам вычислить дивергенцию в отдельно взятых точках, и возникает вопрос: а можно ли подсчитать суммарную дивергенцию по всему телу?
Можно. С помощью тройного интеграла ![]() , который объединяет значения
, который объединяет значения ![]() (элементарные потоки) через все бесконечно малые кусочки
(элементарные потоки) через все бесконечно малые кусочки ![]() тела
тела ![]() .
.
И теперь мы подошли к замечательной формуле Гаусса-Остроградского. Иногда её называют формулой Остроградского-Гаусса, иногда просто формулой Остроградского. Поток векторного поля через замкнутую поверхность ![]() в направлении внешней единичной нормали
в направлении внешней единичной нормали ![]() равен дивергенции данного поля, вычисленной по телу
равен дивергенции данного поля, вычисленной по телу ![]() , которое эта поверхность ограничивает:
, которое эта поверхность ограничивает:
![]()
Следует отметить, что в оригинале формула приводится в обратном порядке, и её краткий смысл таков: интеграл ![]() объединяет дивергенцию по всей области
объединяет дивергенцию по всей области ![]() , и если в ней есть ТОЛЬКО источники или ТОЛЬКО стоки, то происходит их суммирование. Если же там есть и то, и другое, то интеграл «взаимоуничтожает» элементарные потоки (дивергенции) разных знаков. Таким образом, во всех случаях в «сухом остатке» получается поток
, и если в ней есть ТОЛЬКО источники или ТОЛЬКО стоки, то происходит их суммирование. Если же там есть и то, и другое, то интеграл «взаимоуничтожает» элементарные потоки (дивергенции) разных знаков. Таким образом, во всех случаях в «сухом остатке» получается поток ![]() через внешнюю поверхность.
через внешнюю поверхность.
Однако формула чаще используется так, как она записана выше – чтобы трудоёмкое исследование поверхности заменить вычислением банального тройного интеграла. В частности, если функция ![]() представляет собой ненулевую константу, то всё дело, по сути, сводится к вычислению объёма тела.
представляет собой ненулевую константу, то всё дело, по сути, сводится к вычислению объёма тела.
…вы когда-нибудь думали, что будете так рады тройным интегралам? =)
Вернёмся к эпичному Примеру 1, где у нас получился нулевой поток через пирамиду, и вычислим дивергенцию векторного поля ![]() . Очевидно, что само поле и производные его компонент определены не только в пирамиде
. Очевидно, что само поле и производные его компонент определены не только в пирамиде ![]() , но и вообще во всём пространстве:
, но и вообще во всём пространстве:
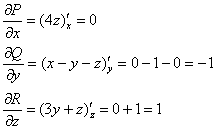
Составим скалярную функцию дивергенции, или как чаще говорят – найдём дивергенцию:
![]()
Полученная функция каждой точке пространства ставит в соответствие ноль, значит векторное поле ![]() всюду соленоидально. По формуле Гаусса-Остроградского, поток векторного поля через внешнюю сторону пирамиды
всюду соленоидально. По формуле Гаусса-Остроградского, поток векторного поля через внешнюю сторону пирамиды ![]() равен:
равен:
![]()
Примечание: т.к. поле бездивергентно во всём пространстве, то поток равен нулю и через любую замкнутую поверхность
Огорчаться, однако, не стОит, поскольку если уж от вас потребовали вычислить поток первым способом, то никуда не деться =) А требуют, между прочим, частенько.
И здесь ещё нужно подчеркнуть следующее: если вы вычислили поток через замкнутую поверхность, и у вас получился ноль, то это ещё не значит, что в области нет источников и стоков. Они могут и существовать, но компенсировать друг друга. И первый способ решения не даёт нам ответ на этот вопрос.
Поэтому решаем второй пример вторым способом:)
Пример 2
Проверить, будет ли векторное поле ![]() соленоидальным, и найти его поток через замкнутую поверхность
соленоидальным, и найти его поток через замкнутую поверхность ![]() по формуле Гаусса-Остроградского
по формуле Гаусса-Остроградского
![]()
Результаты должны совпасть. Обращаю внимание, что проверка поля на соленоидальность является неотъемлемой частью задания, и на этот вопрос нужно дать аргументированный письменной ответ. Примерный образец решения в конце урока, и что приятно – задачу можно оформить в минималистичном стиле, без лишних обозначений и даже без записи самой формулы.
Ну а теперь я расскажу вам, а точнее напомню универсальный метод нахождения нормальных векторов поверхности:
Пример 3
Дано векторное поле ![]() и замкнутая поверхность
и замкнутая поверхность ![]() . Вычислить поток векторного поля через данную поверхность в направлении внешней нормали:
. Вычислить поток векторного поля через данную поверхность в направлении внешней нормали:
а) непосредственно;
б) по формуле Гаусса-Остроградского.
Распространённая формулировка, позволяющая ещё раз осознать всю ценность формулы =)
Решение: чертёж здесь прост:
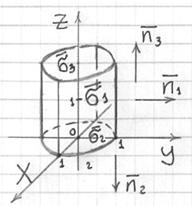
но вот решение – «труба» =)
а) Найдём поток векторного поля через полную поверхность ![]() цилиндра в направлении внешней нормали напрямую. В силу аддитивности поверхностного интеграла:
цилиндра в направлении внешней нормали напрямую. В силу аддитивности поверхностного интеграла:
![]() , где:
, где:
![]() – боковая поверхность цилиндра
– боковая поверхность цилиндра ![]() ;
;
![]() – его нижнее основание (единичный круг в плоскости
– его нижнее основание (единичный круг в плоскости ![]() );
);
![]() – и верхнее основание (единичный круг в плоскости
– и верхнее основание (единичный круг в плоскости ![]() ).
).
1) Цилиндрическая поверхность ![]() параллельна оси
параллельна оси ![]() и возникает вопрос, как найти её векторы нормали? Очень просто. Вектор нормали к поверхности
и возникает вопрос, как найти её векторы нормали? Очень просто. Вектор нормали к поверхности ![]() в точке
в точке ![]() задаётся следующим образом:
задаётся следующим образом:
![]()
В данном случае:
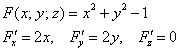
Таким образом, мы получаем целую функцию нормальных векторов для различных точек цилиндра:
![]()
Но нам нужны единичные векторы. Они разыскиваются стандартно:
![]()
Контроль: 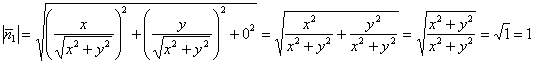
Да, убедимся, что они «смотрят» вовне. Для этого можно взять несколько конкретных точек поверхности (проще всего в плоскости ![]() ) и посмотреть, какие векторы будут получаться. Так, например, для точки
) и посмотреть, какие векторы будут получаться. Так, например, для точки ![]() получаем:
получаем:
![]() – всё ОК. Собственно, этот вектор в качестве примера и изображён на чертеже. Самостоятельно проверьте какие-нибудь другие точки, и удостоверьтесь, что получаются векторы нужного направления.
– всё ОК. Собственно, этот вектор в качестве примера и изображён на чертеже. Самостоятельно проверьте какие-нибудь другие точки, и удостоверьтесь, что получаются векторы нужного направления.
Далее всё идёт по накатанной колее. Вычислим скалярное произведение:
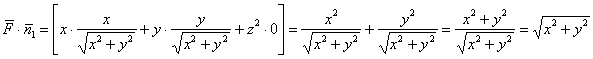
и сведём решение к поверхностному интегралу 1-го рода:
![]()
В данном случае плоскость ![]() не годится для проецирования. Почему? Потому что цилиндрическая поверхность спроецируется в окружность нулевой площади и получится ноль. Но из боковой же поверхности торчат векторы поля, и через неё запросто может идти поток!
не годится для проецирования. Почему? Потому что цилиндрическая поверхность спроецируется в окружность нулевой площади и получится ноль. Но из боковой же поверхности торчат векторы поля, и через неё запросто может идти поток!
Поэтому в нашем распоряжении остаются две координатные плоскости, я выберу для проецирования более наглядную фронтальную плоскость ![]() . И тут возникает другая трудность – цилиндрическую поверхность
. И тут возникает другая трудность – цилиндрическую поверхность ![]() , а значит, и полученный интеграл 1-го рода придётся разделить на 2 части:
, а значит, и полученный интеграл 1-го рода придётся разделить на 2 части:
![]() , где:
, где:
![]() – ближний к нам кусок цилиндра, а
– ближний к нам кусок цилиндра, а ![]() – дальний его кусок.
– дальний его кусок.
Проведём вычисления для первого интеграла:
![]()
Используем соответствующую формулу:
![]() , где:
, где:
![]()
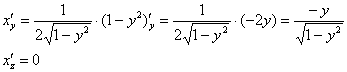
По формуле:

Проекция на плоскость ![]() очевидна:
очевидна:
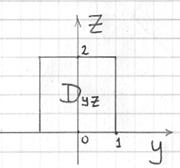
Выберем следующий порядок обхода области:
![]()
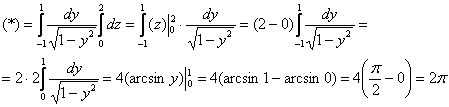
При вычислении второго интеграла получится точно такой же результат:
![]()
Таким образом: ![]()
Это я привел длинное общее решение (на всякий случай), но на самом деле тут есть короткий и изящный путь – в сумму интегралов можно сразу подставить ![]() и
и ![]() :
:
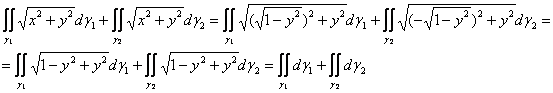
и, согласно геометрическому смыслу этих интегралов, получаем сумму площадей соответствующих поверхностей, которая равна площади боковой поверхности цилиндра: ![]() . Следует заметить, что если радиус цилиндра не равен единице, то перед каждым интегралом появится дополнительный множитель, равный этому радиусу.
. Следует заметить, что если радиус цилиндра не равен единице, то перед каждым интегралом появится дополнительный множитель, равный этому радиусу.
Знание – сила!
2) Вычислим поток векторного поля через ориентированный единичный круг ![]() .
.
С нормалью и скалярным произведением всё просто:
![]()
![]()
а с поверхностным интегралом – ещё проще:
![]() , поскольку
, поскольку ![]()
3) Третий интеграл начинается похоже:
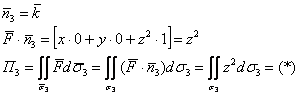
Используем формулу ![]() , в данном случае:
, в данном случае: ![]()
![]()
Проекция ![]() (поверхности
(поверхности ![]() на плоскость
на плоскость ![]() ) представляет собой круг площади
) представляет собой круг площади ![]() , и согласно геометрическому смыслу интеграла
, и согласно геометрическому смыслу интеграла ![]() :
:
![]()
И, наконец, поток через всю поверхность:
![]()
Ответ: ![]()
Что, кстати, означает этот результат? Положительный поток через внешнюю поверхность означает, что внутри цилиндра есть источники поля. Иначе, откуда бы там взяться ![]() единицам жидкости, которые вытекли наружу? (за единицу времени)
единицам жидкости, которые вытекли наружу? (за единицу времени)
б) Решим задачу по формуле Гаусса- Остроградского:
И, прежде всего, тут нужно убедиться, что компоненты ![]() и их производные
и их производные ![]() определены во всех точках тела. В противном случае формулу применять нельзя! Должен предупредить, что это не пустая формальность – на практике встречаются поля с корнями и логарифмами, и вот там могут быть проблемы.
определены во всех точках тела. В противном случае формулу применять нельзя! Должен предупредить, что это не пустая формальность – на практике встречаются поля с корнями и логарифмами, и вот там могут быть проблемы.
Составим функцию дивергенции:
![]() , которую очень полезно проанализировать:
, которую очень полезно проанализировать:
При увеличении «зет» от 0 до 2 дивергенция строго положительна и нарастает. Это означает то, что, во-первых, внутри цилиндра находятся исключительно источники поля. И, во-вторых, эти источники усиливаются, т.е. текущая снизу вверх жидкость начинает разгоняться. Поэтому сразу можно сказать, что поток через внешнюю поверхность будет положительным. В чём мы сейчас ещё раз убедимся аналитически:
![]()
Поскольку проекция тела на плоскость ![]() представляет собой круг единичного радиуса (чертить уж не буду), то удобно перейти к цилиндрической системе координат:
представляет собой круг единичного радиуса (чертить уж не буду), то удобно перейти к цилиндрической системе координат:
![]()
с очевидным порядком обхода тела:
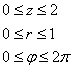

Ответ: ![]()
Теперь вам, наверное, понятно, почему поверхностные интегралы и теория поля встречаются далеко не во всех учебниках по математическому анализу =)
Для самостоятельного решения:
Пример 4
Вычислить поток векторного поля ![]() через замкнутую поверхность
через замкнутую поверхность ![]() в направлении внешней нормали.
в направлении внешней нормали.
По умолчанию, разумеется, лучше выбрать более лёгкий путь, который представлен в образце решения. Но любителям математического анализа, наверное, будет интересно попробовать вычислить поток и непосредственно. И это ни в коем случае не чёрный юмор – среди посетителей сайта немало желающих «потягаться» с трудными задачами.
Формула Остроградского-Гаусса может помочь и достаточно неожиданным образом. Вспомним Пример 7 урока Поверхностные интегралы с трудным-трудным вычислением внешнего потока через полусферу ![]() . В случае непреодолимых трудностей с таким решением, существует окольный путь: сначала находим внешний поток через полную поверхность верхней половины шара, затем вычитаем из него поток, вычисленный через круг
. В случае непреодолимых трудностей с таким решением, существует окольный путь: сначала находим внешний поток через полную поверхность верхней половины шара, затем вычитаем из него поток, вычисленный через круг ![]() в направлении вектора
в направлении вектора ![]() .
.
И в заключение статьи я всегда стараюсь подобрать «гвоздь программы» – что-то новое, что-то яркое, и что-то воздушное:)
Сферическая система координат
До сих пор мы использовали цилиндрическую систему координат, которая, по технической сути, представляет собой «плоскую» полярную систему + дополнительную координату «зет». Но произвольную точку ![]() пространства бывает удобно определить и по-другому, а именно расстоянием
пространства бывает удобно определить и по-другому, а именно расстоянием ![]() от начала координат и двумя углами:
от начала координат и двумя углами:
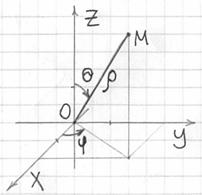
Угол ![]() называется зенитным и отсчитывается от полуоси
называется зенитным и отсчитывается от полуоси ![]() . Данный угол изменяется в пределах
. Данный угол изменяется в пределах ![]() и крайнему значению
и крайнему значению ![]() соответствуют точки, лежащие на нижней полуоси
соответствуют точки, лежащие на нижней полуоси ![]() .
.
Угол ![]() называется азимутальным и отсчитывается в плоскости
называется азимутальным и отсчитывается в плоскости ![]() против часовой стрелки. Он изменяется в пределах
против часовой стрелки. Он изменяется в пределах ![]() , иными словами, «ведёт» себя точно так же, как полярный угол.
, иными словами, «ведёт» себя точно так же, как полярный угол.
Таким образом, с помощью «ро», «тета» и «фи» можно однозначно определить любую точку пространства.
Где используется сферическая система координат? Ну, конечно же, в астрономии. Но своё скромное применения она нашла и при вычислении тройных интегралов:
Пример 5
Вычислить поток векторного поля ![]() через замкнутую поверхность
через замкнутую поверхность ![]() (нормаль внешняя)
(нормаль внешняя)
Решение: тот редкий случай, когда можно обойтись без чертежа. Однако я всё же втайне мечтаю, что потомки оценят художественную ценность моих сканов:)
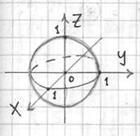
Поскольку компоненты ![]() и их очевидные производные
и их очевидные производные
![]() определены во всех точках шара (и вообще всюду), то мы вправе воспользоваться формулой Гаусса-Остроградского.
определены во всех точках шара (и вообще всюду), то мы вправе воспользоваться формулой Гаусса-Остроградского.
Составим функцию ![]() и по соответствующей формуле вычислим поток векторного поля через сферу во внешнем направлении:
и по соответствующей формуле вычислим поток векторного поля через сферу во внешнем направлении:
![]()
Перейдём к сферической системе координат. Формулы перехода к ней таковы:
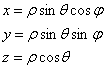
И давайте сразу преобразуем подынтегральную функцию:
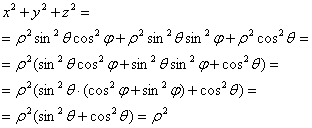
Произведение трёх дифференциалов превращается в следующую вещь:
![]() , где «добавка»
, где «добавка» ![]() – это «плата за переход» (Якобиан перехода).
– это «плата за переход» (Якобиан перехода).
Осталось определиться с порядком обхода тела. Ещё раз посмотрите на чертёж или нарисуйте шар в уме. Как учитываются все его точки? Представьте это в динамике:
– сферический радиус (расстояние от центра) изменяется в пределах ![]() , при этом зенитный угол проходит все свои значения:
, при этом зенитный угол проходит все свои значения: ![]() и получившийся полукруг с диаметром на оси
и получившийся полукруг с диаметром на оси ![]() совершает полный оборот вокруг этой оси:
совершает полный оборот вокруг этой оси: ![]()
Остальное дело техники – переход к повторным интегралам и финальные вычисления:

Тройной интеграл можно было взять и через цилиндрические координаты, но вычисления получились бы заметно труднее.
Ответ: ![]()
Положительный поток был предсказуем, т.к. поле ![]() имеет источники вообще во всех точках, кроме начала координат:
имеет источники вообще во всех точках, кроме начала координат: ![]() .
.
Когда удобно использовать сферическую систему координат?
Когда нет проблем с определением зенитного угла. Как правило, это сфера и её части, сфера, вложенная в другую сферу и т.п. конструкции. Кстати, шаровой сектор из Примера 4 – там этот угол прям конфетка: ![]() , и желающие могут вычислить тройной интеграл вторым способом. Но само по себе использование ССК ещё не означает, что решение получится проще.
, и желающие могут вычислить тройной интеграл вторым способом. Но само по себе использование ССК ещё не означает, что решение получится проще.
Спасибо за внимание, надеюсь, данная статья была полезной! Вы не просто молодцы, а самые настоящие герои:) – потому что материал о поверхностных интегралах, потоке и дивергенции действительно сложноват.
Жду вас на заключительном уроке по теме под названием Циркуляция векторного поля.
Решения и ответы:
Пример 2: Решение: найдём дивергенцию векторного поля:
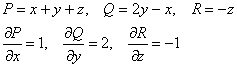
![]() , значит, поле
, значит, поле ![]() не является соленоидальным.
не является соленоидальным.
Выполним чертёж:
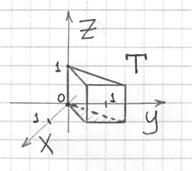
Поток векторного поля через внешнюю поверхность призмы вычислим по формуле Гаусса-Остроградского:
![]()
Изобразим проекцию тела на плоскость ![]() :
:
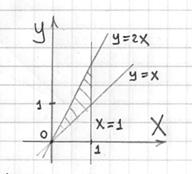
Выберем следующий порядок обхода тела:
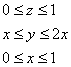
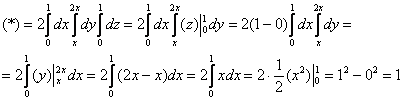
Ответ: поле не является соленоидальным, ![]()
Пример 4. Решение: найдём линию пересечения конической поверхности и сферы:
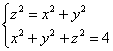 – подставим
– подставим ![]() во 2-е уравнение:
во 2-е уравнение:
![]()
![]()
Таким образом, на высоте ![]() конус пересекается со сферой по окружности
конус пересекается со сферой по окружности ![]() . Изобразим на чертеже искомую поверхность, ограниченное ей тело
. Изобразим на чертеже искомую поверхность, ограниченное ей тело ![]() и его проекцию на плоскость
и его проекцию на плоскость ![]() :
:
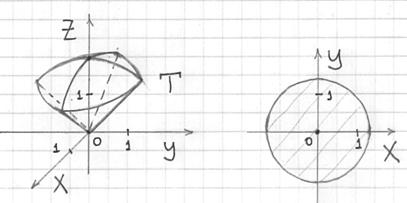
Поток векторного поля через замкнутую поверхность вычислим по формуле Гаусса-Остроградского. Найдём дивергенцию векторного поля:
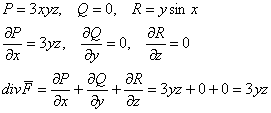
Таким образом:
![]()
Перейдём к цилиндрической системе координат:
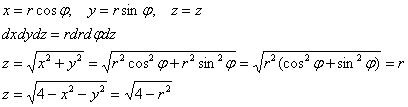
Порядок обхода тела:
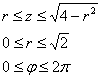

Ответ: ![]()
Примечание 1: такой результат означает, что внутри тела есть источники и стоки поля (т.к. функция ![]() ), но они компенсируют друг друга.
), но они компенсируют друг друга.
Примечание 2: при вычислении 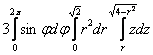 можно было сразу взять интеграл
можно было сразу взять интеграл 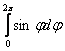 и получить ноль (т.к. во внутренних интегралах от «фи» ничего не зависит), однако такое решение одобрят далеко не все рецензенты.
и получить ноль (т.к. во внутренних интегралах от «фи» ничего не зависит), однако такое решение одобрят далеко не все рецензенты.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright