Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Как найти производную?
Примеры решений

Как найти производную, как взять производную? На этих уроках мы научимся находить производные функций. Для освоения материала потребуется Таблица производных (откроется в новой вкладке), и по возможности её лучше распечатать – так будет гораздо удобнее. К таблице придётся обращаться часто, в том числе в оффлайне.

...Есть? Приступим. У меня для Вас есть две новости: хорошая и очень хорошая.

Хорошая новость состоит в следующем: чтобы научиться находить производные, совсем не обязательно знать и понимать, что такое производная. Более того, с теорией даже лучше повременить. Очень хорошая новость состоит в том, что научиться брать производные не так сложно, существует довольно чёткий алгоритм решения (и объяснения) этого задания, интегралы или пределы, например, освоить труднее.

Советую следующий порядок изучения темы. Во-первых, эта статья. содержание:

• Алгоритм нахождения производных. Простейшие примеры.
  
• Вынос константы из-под знака производной
• Как найти производную сумму / разности?
• Как найти производную произведения?
• Как найти производную частного?

…Ссылки-таки проставлять не стал, тут всё рядом, всё быстро.

Затем нужно изучить важнейший урок Производная сложной функции. Эти два базовых занятия позволят поднять Ваши навыки с полного нуля.

Далее можно будет ознакомиться с более сложными производными в статье Сложные производные. Логарифмическая производная. Если планка окажется слишком высокА, то сначала прочитайте Простейшие типовые задачи с производной. Помимо нового материала, на уроке рассмотрены другие, более простые типы производных, и есть прекрасная возможность улучшить свою технику дифференцирования. Кроме того, в контрольных работах почти всегда встречаются задания на нахождение производных функций, которые заданы неявно или параметрически, не обходим вниманием!

Для тех, у кого ОЧЕНЬ мало времени, есть интенсивный курс в pdf-формате. Также записан видеокурс – для скорейшего освоения практики онлайн.

И сейчас я попытаюсь в доступной форме, шаг за шагом, научить Вас находить производные функций. Вся информация изложена подробно, простыми словами.

Собственно, сразу рассмотрим:

Пример 1

Найти производную функции

Решение:

Пожалуйста, найдите эту производную в таблице. Теперь посмотрим на решение и проанализируем, что же произошло? А произошла следующая вещь: у нас была функция , которая в результате решения превратилась в функцию .

Говоря совсем просто, для того чтобы найти производную функции, нужно по определённым правилам превратить её в другую функцию. Посмотрите еще раз на таблицу производных – там функции превращаются в другие функции. Единственным исключением является экспонента , которая превращается сама в себя.

Операция нахождения производной называется дифференцированием.

Обозначения: производную обозначают или (читается «дэ игрек по дэ икс»).

ВНИМАНИЕ, ВАЖНО! Забыть поставить штрих (там, где надо), либо нарисовать лишний штрих (там, где не надо) – ГРУБАЯ ОШИБКА! Функция и её производная – это две разные функции!

Вернёмся к нашей таблице производных. Из неё лучше сразу запомнить наизусть:

производную константы:
, где  – постоянное число;

производную степеннОй функции:
,  в частности: , , .

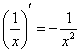Зачем запоминать? Данные знания являются элементарными знаниями о производных. И если Вы не сможете ответить преподавателю на вопрос «Чему равна производная числа?», то учеба в ВУЗе может для Вас закончиться (лично знаком с двумя реальными случаями). Кроме того, это наиболее распространенные формулы, которыми приходится пользоваться практически каждый раз, когда мы сталкиваемся с производными.

Но то была демонстрация. В реальности простые табличные примеры – редкость, обычно при нахождении производных сначала используются правила дифференцирования, а затем – таблица производных элементарных функций.

В этой связи переходим к рассмотрению правил дифференцирования, которые, как вы заметили :), приведены в том же файле.

1) Множитель-число можно (и нужно) вынести за знак производной

, где  – число (константа)

Пример 2

Найти производную функции

Смотрим в таблицу производных. Производная косинуса там есть, но у нас .

Решаем:

Самое время использовать правило, выносим постоянный множитель за знак производной:

А теперь превращаем наш косинус по таблице:

Ну и результат желательно немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:

Готово.

2) Производная суммы равна сумме производных

Напоминаю, что разность – это алгебраическая сумма, вместо «из этого вычесть это», всегда можно сказать «к этому прибавить минус это».

Пример 3

Найти производную функции

Решаем. Как Вы, наверное, уже заметили, первое действие, которое выполняется при нахождении производной, состоит в том, что мы заключаем в скобки всю исходную функцию и ставим штрих справа вверху:

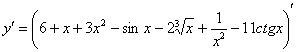
Применяем второе правило:

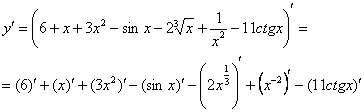
Для дифференцирования корень удобно представить  в виде , а степень из знаменателя – переместить наверх. Если позабылось как, то освежите в памяти Горячие школьные формулы; к слову, справочные материалы у нас хранятся на отдельной странице (новоприбывшим читателям).

Теперь вспоминаем о первом правиле дифференцирования – постоянные множители (числа) выносим за знак производной:

Обычно в ходе решения эти два правила применяют одновременно (чтобы не переписывать лишний раз длинное выражение).

Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение:

Можно всё оставить в таком виде, так как штрихов больше нет, и производная найдена. Тем не менее, подобные выражения обычно упрощают:

Все степени вида  желательно снова представить в виде корней, а степени с отрицательными показателями – сбросить в знаменатель. Хотя этого можно и не делать, ошибкой не будет.

Пример 4

Найти производную функции

Попробуйте решить данный пример самостоятельно (ответ в конце урока).

3) Производная произведения функций

Вроде бы по аналогии напрашивается формула …., но неожиданность состоит в том, что:

Это необычное правило (как, собственно, и другие) следует из определения производной. Однако теория подождёт – сейчас важно научиться решать:

Пример 5

Найти производную функции

Здесь у нас произведение двух функций, зависящих от .

Сначала применяем наше странное правило, а затем превращаем функции по таблице производных:

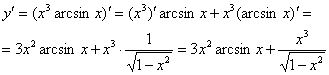
Сложно? Вовсе нет, вполне доступно даже для чайника.

Пример 6

Найти производную функции

В данной функции содержится сумма  и произведение двух функций –  квадратного трехчлена   и логарифма . Со школы мы помним, что умножение и деление имеют приоритет перед сложением и вычитанием.

Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:

Теперь для скобки  используем два первых правила:

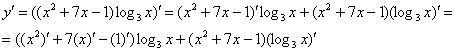
В результате применения правил дифференцирования под штрихами у нас остались только элементарные функции, по таблице производных превращаем их в другие функции:

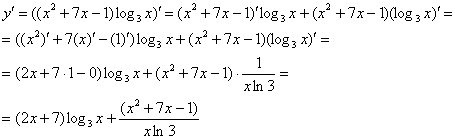
Готово.

При определенном опыте нахождения производных, простые производные вроде не обязательно расписывать так подробно. Вообще, они обычно решаются устно, и сразу записывается, что .

Пример 7

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока)

4) Производная частного функций

В потолке открылся люк, не пугайся, это глюк.

А вот это вот суровая действительность:

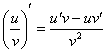
Пример 8

Найти производную функции

Чего здесь только нет – сумма, разность, произведение, дробь…. С чего бы начать?! Есть сомнения, нет сомнений, но, В ЛЮБОМ СЛУЧАЕ для начала рисуем скобочки и справа вверху ставим штрих:

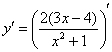
Теперь смотрим на выражение в скобках, нельзя ли его упростить? В данном случае замечаем множитель-константу, который, согласно первому правилу, целесообразно вынести за знак производной:

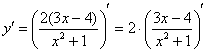– заодно избавляемся от скобок в числителе, которые теперь не нужны.

Вообще говоря, постоянные множители при нахождении производной можно и не выносить, но в этом случае они будут «путаться под ногами», что загромождает и затрудняет решение.

Смотрим на наше выражение в скобках. У нас есть сложение, вычитание и деление. Со школы мы помним, что деление выполняется в первую очередь. И здесь – сначала применяем правило дифференцирования частного:

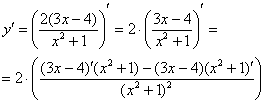
Таким образом, наша страшная производная свелась к двум простеньким штрихам. Применяем первое и второе правило, здесь это сделаем устно, надеюсь, Вы уже немного освоились в производных:

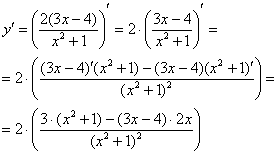
Штрихов больше нет, задание выполнено.

На практике обычно (но не всегда) ответ упрощают «школьными» методами:

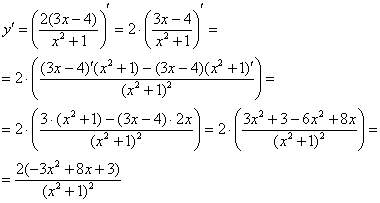
Пример 9

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Время от времени встречаются хитрые задачки:

Пример 10

Найти производную функции

Смотрим на данную функцию. Здесь снова дробь. Однако перед тем как использовать правило дифференцирования частного (а его можно использовать), всегда имеет смысл посмотреть, а нельзя ли упростить саму дробь, или вообще избавиться от нее? Дело в том, что формула 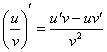 достаточно громоздка, и применять ее совсем не хочется.

В данном случае можно почленно поделить числитель на знаменатель. Преобразуем функцию:

Ну вот, совсем другое дело, теперь дифференцировать просто и приятно:

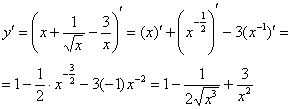
Готово.

Пример 11

Найти производную функции

Здесь ситуация похожа, превратим нашу дробь в произведение, для этого поднимем экспоненту в числитель, сменив у показателя знак:

Произведение всё-таки дифференцировать проще:

Пример 12

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

5) Производная сложной функции

Данное правило также встречается очень часто. Но о нём рассказать можно очень много, поэтому я создал отдельный урок на тему Производная сложной функции.

Желаю успехов!

Ответы:

Пример 4: . В ходе решения данного примера следует обратить внимание на тот факт, что  и  – это константы, не важно чему они равны, важно, что это числа. Поэтому  выносится за знак производной, а .

Пример 7:

Пример 9:

Пример 12:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте